晶体表面附近光的偏振态的理论研究

张丽琴，徐士涛

（淮北师范大学 物理与电子信息学院，安徽 淮北 235000）

1 引言

光的偏振性质已经被广泛应用到很多领域，包括生物学、光通信等.对于光的偏振态的研究在物理光学史上占据着举足轻重的地位.而对于晶体表面附近光的偏振态的理论研究也具有深远的实际意义.光在晶体会发生双折射现象，而光的折射、反射又会对光的偏振态产生影响，本文就是基于晶体表面附近光会发生双折射现象，进而对光的偏振态产生影响，从而对晶体表面附近光的偏振态进行研究[1].首先是马吕斯通过实验得出了光是横波，而且还进一步研究了光的偏振特性.物理学史上第一个偏振片是由哈佛大学的一个叫land的学生于1928年发明的.目前光的偏振技术已经在光通信、电子、材料、液晶、光调剂等诸多领域得到了充分的应用，与生活息息相关，所以各国科学家都非常重视，并精心研究，以发掘光的偏振技术在其他的应用领域和发展潜力.国内主要运用的表示方法有菲涅尔公式和偏振光的Jones矢量，由此得到光在介质表面反射、折射的Jones矩阵，对晶体表面附近光的偏振态进行理论研究.而国外的主力军主要R.M.A.Azzam,Hauge,Krishnan等，他们主要利用分振幅光偏振仪测量待测光的全部斯托克斯参数进行研究[2].

2 光的偏振态

2.1 光的偏振态及其区分

光波的电场和磁场的两个分量都是和光波的传播的方向垂直的，而正是光波的这一特性引起了光的偏振.光有五种可能的偏振态：（1）自然光；（2）线偏振光；（3）部分偏振光；（4）圆偏振光；（5）椭圆偏振光.自然光作为偏振光的特性有：两束光的振幅是相等的，振动方向是相互垂直的，并且它们的相位关系是不确定的.如果有一种光，它的光矢量有且只有一个振动方向，而且这个振动方向在光的整个传播过程一直都是一成不变的，不过它的光矢量的大小会随着相位的变化而变化，这种光称为线偏振光.还有一种光在传播过程中的各项物理性质都处于自然光和线偏振光两者之间，这种光即为部分偏振光.还有一种光，它的光矢量不会发生改变，但是它的振动方向会围绕光传播的轴线有规律的转动，从而能得到一个运动轨迹是圆的光，即为圆偏振光.同上，光在传播过程中，矢量的大小和方向都不会发生变化的一种光，即为椭圆偏振光.它的矢端的运动轨迹是一个椭圆.

区分：圆偏振光和椭圆偏振光可以看成电场矢量正交，有恒定相位差的两个一样频率的线偏振光的叠加；圆偏振光、线偏振光实际上都属于特殊的椭圆偏振光，因为这两种光都是它的两种特殊形式.

2.2 光的偏振态的数学表示

2.2.1 相位差、振幅比表示

圆偏振光、椭圆偏振光可以由两个线偏振光合成，不过这两个线偏振光需要是沿着同一个方向传播的.而根据光的几种偏振态的区分，我们可以用一般情况下椭圆偏振光的数学表示来研究光的偏振态.椭圆方程为：

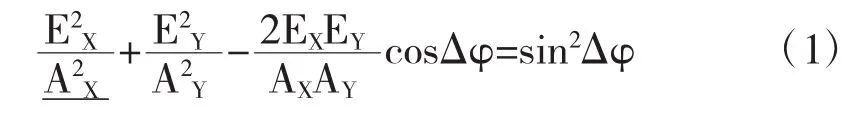
其中，Ex、Ey分别是z轴方向传播的偏振光在x、y轴的电场分量，Ax、Ay分别是对应的谐振幅.

2.2.2 琼斯矢量表示法

首先建立一个坐标系，再将一束偏振光电场矢量分解为两坐标轴上的分量，并且可以用矩阵表示：

上式即为琼斯矢量，利用辅助参量即可化为：

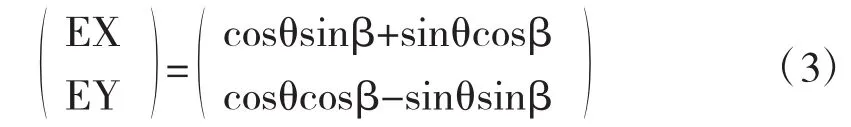
我们利用这种矩阵简化的方式演示了偏振光，比如说偏振态的叠加，我们即可用琼斯矢量矩阵相加即可.特别是，当我们对其进行简单处理后，还能够得到复平面和复矢量的描述方法，而且涉及在不同的介质和不同的器件偏振光的传输时，想要得到偏振终态的方法非常简单，仅仅把器件的琼斯矩阵进行相乘就行了.这对于偏振光的传输分析非常便捷.需要注意的是，它只是对于光电场振幅的描述，而对于光强并不适用[3].

2.2.3 邦加球表示法

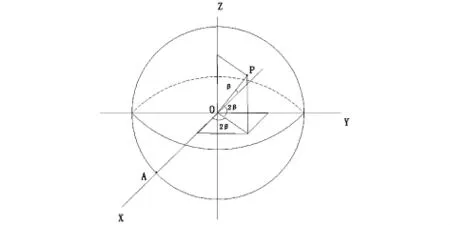
图1 邦加球表示图

如上图1，如果2β等于零，那么上图中表示线偏振光的点在赤道上面，在点 A 上，2β=0，2θ=0，表示的是图中x轴方向上的，与A对称的B上，如果2β=0，2θ=P，即为 y轴方向上的线偏振光，北极上，2β为零，即为右旋圆偏振光.地球上面的每一个点，都可以是一个偏振态[4].

2.2.4 史密斯圆图

上述的邦加球表示法使用在三维空间中，并不是十分方便.那么在二维空间，我们使用的是：史密斯圆图.

它是邦加球三维视图的平面投影图（从上往下看）.A和B两点分别表示x、y轴方向的线偏振光，而且圆周上的任意一点即为线偏振光，圆心即为圆偏振光，其他的任意一点就是椭圆偏振光[5].

由此我们可以证明，椭圆偏振光有：

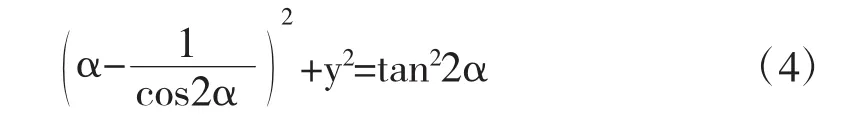
等相位差的线方程为

等椭圆度方程

等长轴方位线方程

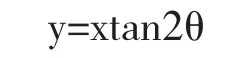
振幅的比一样的线为：等a线，相位差一样的线是：等δ线，长轴、短轴的比一样的线是：等γ线，长轴、x轴之间的一个角叫做等θ线.

在圆周上面的每一个点，线偏振光可以是δ=0或π，而且β=0的一个点.而在A点：x方向振动的线偏振光可以用ay=0表示；b点：y方向振动的线偏振光可以用ax=0；在圆心c处：圆偏振光的表示要用，也就是振幅的比是1，与此同时也有相位差；椭圆偏振光则可以用在圆内部的各个点表示.

3 晶体表面附近光的偏振态

3.1 反射折射引起的偏振态的变化

光在两个介质之间的分界面发生反射和折射的时候，我们用菲涅尔公式来表示振幅的变化.

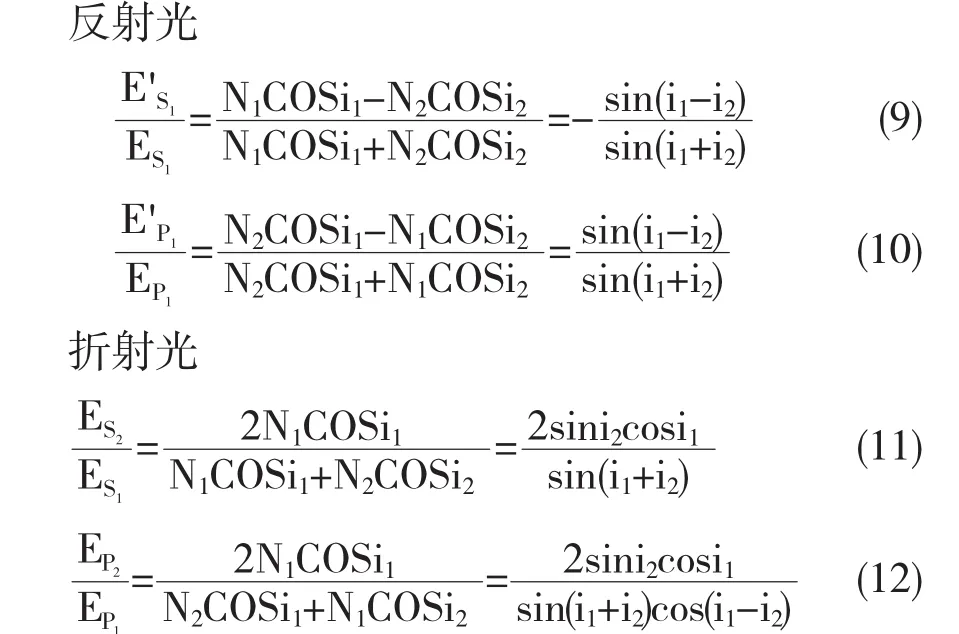
3.1.1 垂直入射

根据菲涅尔公式，在光垂直入射的时候，当i1=0 的时候，i2=0，所以有

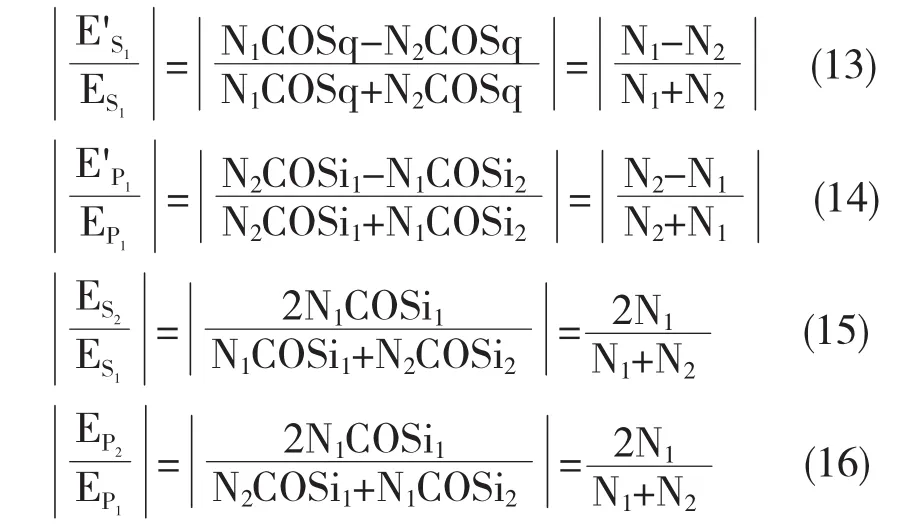
据此可知

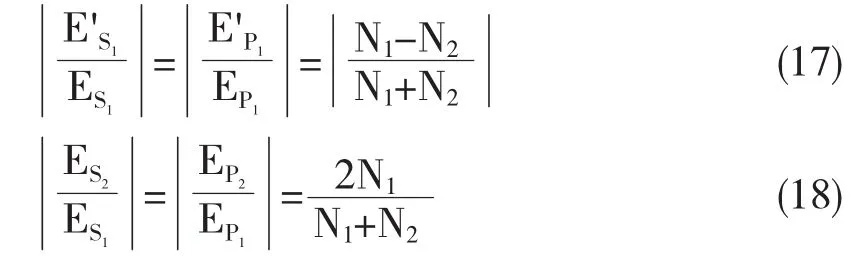
上述式（13）（14）（15）（16）表述的是：不管是反射光还是折射光，每一个分量的变化一定成比例.又因为垂直入射的时候，入射光、反射光以及折射光具皆与法线是重叠在一起的，所以它们的入射的面不是确定的，即上文提到的两个分量，P分量和S分量是任意的，所以有反射光和折射光的偏振的性质不会发生改变[7].

3.1.2 布儒斯特定律

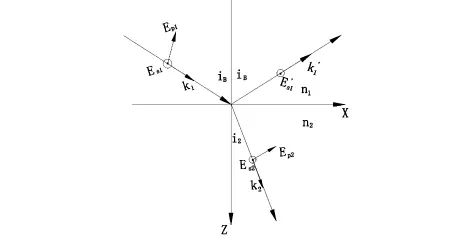
图2 平面偏振光图

如果要使反射光、折射光两者之一能够成为平面偏振光，我们便需要让其中的一个的分量为零.

在这样的情况下即为线偏振光，也就是反射光中只含有S分量.根据折射定律可知，这时必须有

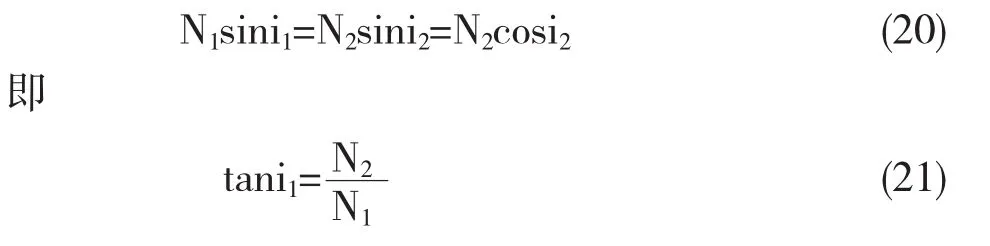
我们把这种情况下的入射角记做ia,那么有

此公式即为布儒斯特定律，ia即为布儒斯特角.

3.2 光在晶体中的双折射

3.2.1 晶体的光学特性

晶体的结构这一物理性质是属于各向异性的，这种性质就是由这种对称性所决定的.因此在晶体里面，沿每一个不同的方向上，都会拥有不同的物理性质，像是介电常数，热传导系数和热膨胀系数等.同样的，透光晶体的各种物理性质也是各向异性的.按照这种对称性，晶体可以划分为十四种布拉伐格子；而这十四种布拉伐格子都同属于七大晶系.如果根据晶体的物理性质，晶体能够分为三大类.

第一类属于立方晶系，这一类都会有三个不同的但相互有正交的结晶学的方向.关于这种晶系，根据上文提到的三个相互正交的结晶学方向是等效的，所以，它们的介电常数和物理性质也一定是相同的，这一点和非晶体是一样的.

第二类就是我们所说的三、四、六角晶系.这一类晶系需要有两个或是两个以上的等效结晶学方向，并且要与这个平面垂直.

第三类晶系包括正交晶系、单斜晶系、三斜晶系三种：这一类晶系没有两个等效的结晶学方向.这一类晶体就叫做双轴晶体.

3.2.2 晶体的双折射

3.2.2.1 双折射的概念

晶体的双折射表示的就是光线射入某种晶体中产生两种折射光线的现象.

3.2.2.2 寻常光（o光）和非寻常光（e光）

晶体的双折射现象产生的两束折射光都是平面偏振光，在各种性质相同的介质中，相同的那束折射光叫做寻常光，遵循折射定律；另一束即为非寻常光，不遵循折射定律.

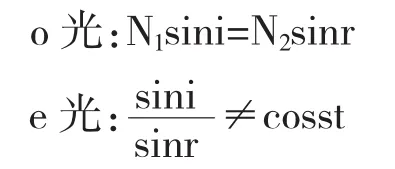
o光矢量的方向垂直于它的主平面；同样，e光的需要和e光光轴平行，所以它在e光的主平面内.

o光、e光的光强：如果光的入射面和光在空间传播的主截面发生重叠，那么晶体中这两个折射光的主平面都会与这两束光的主截面发生重叠，我们可以由此得出这两束光的相对光强.入射光如果是自然光的话，那么晶体中的两束光因为具有不同的折射，o光与e光的光强就会不相等.需要特别注意的是，这两种光在垂直射入晶体的时候，它们的入射角都是零，所以它们即使会在晶体中发生双折射，但是由于这两种光线没有分离，导致这两种折射光在从晶体中射出时，它们的相对光强是确定的.

o光、e光的波面：晶体中如果存在一个波动源，这个波动源会将波动向其他任何一个方向传播.在晶体里面，光的主平面是由光的波线和光轴一起构成的.如果波动的方向和主平面是垂直的，那么这种波动在任何一个方向的速度都是一样的，所以它构成的波面是一个球面，这就是晶体里面的o光；同样的道理，如果晶体中上述两个物理量的方向是平行的，那么这种光就是晶体中的e光（它的波面为椭球面）.

3.2.2.3 双折射晶体

只要能够产生双折射的现象，那么这类晶体就具有各向异性结构.例如，方解石.

在晶体内，除了光轴上的方向，任何一个方向都允许两束相同的线偏振光以不同的传播速度传播，前提是这两个线偏振光的电矢量要保证是相互垂直的[8].

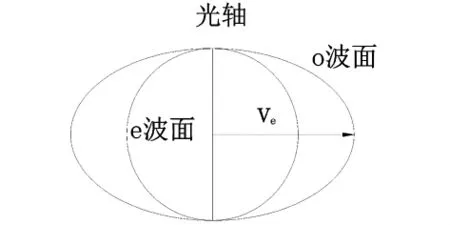
图3 O光、e光波面图

如上图，e光的是一个以光轴对称的回转椭球面，它的方程为

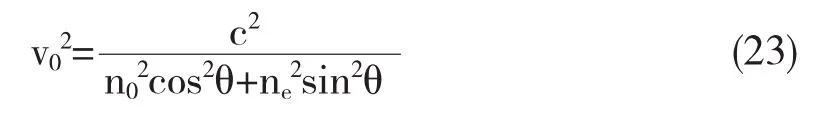
式（23）中c是真空中的光速，n0表示的是o光的折射率，ne代表e光传播时的折射率，θ是e光方向与光轴方向的一个夹角.

特别需要注意的是，在晶体中，e光线的传播速度与传播方向，和正常情况下的相比有所不同，在正常情况下的传播速度，我们把它叫做法线速度[9].法线速度的矢端描绘的空间形状就是法线面，法线面与波面的空间几何关系如下图：

它的方程为：

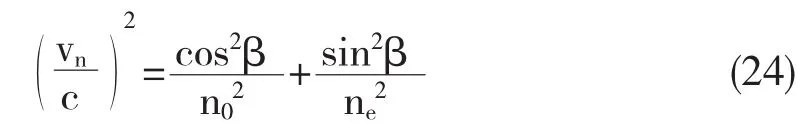
式（24）中vn表示的是法线上的速度，β便是法线上的速度矢量和光轴轴线方向上的一个夹角.法线面在立体空间中是一个曲面[10].

4 结论

本文主要通过介绍光的偏振态的性质，晶体中发生的双折射现象以及反射光、折射光与光的偏振态之间的联系，来研究晶体表面附近光的偏振态的.

首先我们简单介绍了光的五种不同的偏振态，研究了光的偏振态的数学表示方法.通过对光的偏振态的区分，介绍了圆偏振光、椭圆偏振光和线偏振光可以用振幅比、相位差表示，以及琼斯矢量表示法、邦加球表示法、史密斯圆图表示法.随后我们介绍了反射折射对偏振态的影响，光垂直入射时引起的变化和布儒斯特定律.最后我们研究了晶体中的双折射.