线性代数中的一题多解与一题多变
黄新宇
(1.皖西学院 金融与数学学院;2.皖西学院 金融风险智能控制与预警研究中心,安徽 六安 237012)
线性代数作为大学各专业重要的公共基础课之一,同时也是为非数学类专业开设的一门主要基础课和考研必考课.由于这门课程起点不高,但是概念、公式繁多,定义,定理证明较多,缺乏实例,给人的感觉非常抽象并且不实用,这一课程特点给线性代数的教与学习带来一定的难度.因此在教学过程中培养学生的数学学习兴趣和创新思维能力显得尤为重要.创新思维能力的核心是发散思维.什么是发散思维呢?发散思维属于创造性思维,是一种沿不同方向、途径和角度去设想、探求多种答案,最终使得问题获得圆满解决的思维方法[1].“数学的新思维、新概念和新方法主要来源于发散思维”.下面以行列式的计算为例来谈线性代数中一题多解和一题多变.
1 一题多解
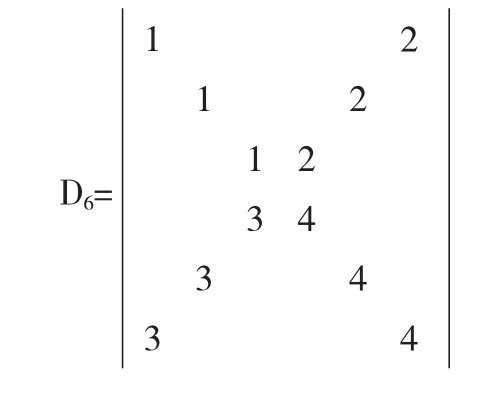
例1计算六阶行列式D6=
分析:该行列式的特点是主对角线和次对角线上只有两种元素,其余元素为0.由于该行列式阶数较高,且具有较低阶的相同结构,于是对行列式降阶从而揭示其内部规律也是我们的一个基本想法,即一个行列式可以用比它低阶的一系列行列式表示,也就是递推法.
解法一:可以将行列式按行(列)展开,展开后可得

都按最后一行展开4D4-6D4=-2D4
由此可得递推公式
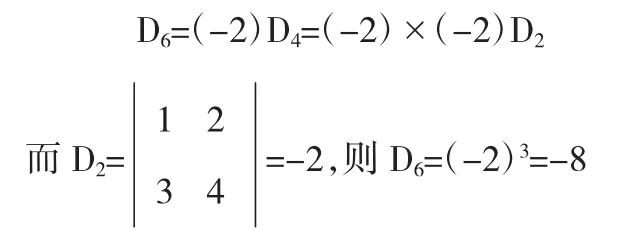
解法二:应用拉普拉斯定理[2]展开行列式,按照第一行和第六行展开,

解法三:先把行列式的第六行依次与第五行…第二行对换(作四次相邻两行的对换),再把行列式中的第六列依次与第五列…第二列对换(作四次相邻两列的对换),得到

解法四:利用分块矩阵计算行列式,
命题1[4]设是一个四方块n阶矩阵,其中A,B,C,D 分别是 r×r,r×(n-r),(n-r)×r,(n-r)×(n-r)阶矩阵,则
(1)若A可逆,则|P|=|A||D-CA-1B|;
(2)若D可逆,则|P|=|D||A-BD-1C|.
将此行列式分成四块

所以根据命题1得

解法五:应用MATLAB数学软件求解.
输入命令:
》A=[1 0 0 0 0 2;0 1 0 0 2 0;0 0 1 2 0 0;0 0 3 4 0 0;0 3 0 0 4 0;3 0 0 0 0 4];
》x=det(A)
输出结果为:
X=-8.000
对上述几种解题方法总结,像这种只有主对角线和次对角线上有元素的行列式的解法一、二和三都是把一个行列式表示为具有相同结构较低阶行列式的线性关系式,再根据此关系递推求得行列式的值.解法四利用分块矩阵化繁为简进行计算,解法五借助数学软件MATLAB编写命令可以得出答案.解法五最为简便,但是数学软件只能计算具体的数字行列式.
通过一题多解一类题目,让学生从不同角度、不同方面去分析思考问题,探索一类题目的解题方法,这样不仅可以扩充思维领域,激发学生的求知欲,还能让学生对问题研究的更加深入.
2 一题多变
如果将例题1中主对角线中的1换成a,4换成d,次对角线中的2换成b,3换成c,可得到变式1:
例2计算六阶行列式D6=
相信学生们已经掌握了这种题型的做法,仿照例1解法可以得到递推公式依次递推可得D6=最后将此行列式推广至2n阶,得到变式2:
例3计算2n阶行列式

其中未写出的元素为0.
这个行列式的特点是只有主对角线和次对角线上有元素,其余元素为零.由于行列式阶数较高,并且行列式中的元素不是具体数字,对于一开始接触行列式计算的大一学生来说,直接去计算例3是有一定的难度.但是如果学生们掌握了例1的解法,从特殊到一般,那就很自然而然地得到例3的答案D2n=(ad-bc)n.
3 结束语
通过一题多解,一题多变开展问题的分析和研究,让学生从一道习题抓一类问题,从特殊到一般,不仅可以取得举一反三,触类旁通的效果,又能使得学生对这种类型习题的解法有了较深刻的印象,有利于掌握这种类型习题的解题方法,从而提高学生的创新思维能力,并逐渐体会到学习的乐趣.

