基于微波光学实验仪研究光的干涉现象

刘 慧，边 健，丰 远，徐 琳

（合肥学院 数理系，安徽 合肥 230601）

1 引言

英国物理学家麦克斯韦于1864年发表了《电磁场的动力学理论》论文，对前人和自己的工作进行概括，建立了电磁波理论，据此预言了电磁波的存在.德国物理学家赫兹于1887年首先用实验证实了电磁波的存在.后来，科学家又发现自然界中存在多种形式的电磁波，它们的频率和波长不同，但本质完全相同.常见的电磁波按频率的大小可以列举为：γ射线＞X射线＞紫外线＞可见光＞红外线＞微波＞视频＞射频.

微波是指频率介于300MHz和300GHz之间的电磁波，即波长在1m（不含1m）到1mm之间的电磁波.随着科学技术的高速发展，微波在通信、勘测、军事、医疗等领域都发挥着越来越重要的作用，并且不断开辟新的研究和应用领域，形成了一系列的交叉科学[1].光的干涉现象指的是两列或几列光波在空间相遇时相互叠加，在某些区域始终加强，在另一些区域则始终削弱，形成稳定的强弱分布的现象.微波作为一种电磁波，其传播规律及其与物质的相互作用与光波一样，因此用微波做干涉实验与用光波做干涉实验所得到的规律是一致的.又由于微波的波长比光波的波长大一万倍以上，因此微波干涉实验比光的干涉实验更直观、安全和方便[2-4].

本实验采用的仪器是成都世纪中科仪器有限公司生产的ZKY-WB-2型微波光学综合实验仪，仪器采用类似光学分光计的设计思想.成套仪器由发射器组件、接收器组件、可旋转载物平台和支架，以及其他实验用附件（反射板、透射板、双缝板、偏振板、棱镜等）等组成.利用此仪器可以研究光学实验中的干涉现象，例如杨氏双缝干涉、劳埃德镜、迈克尔逊干涉以及法布里-珀罗干涉，并可以测定微波波长.下面对这些实验做一介绍.

2 光的干涉现象的实验研究

2.1 杨氏双缝干涉[5,6]

图1 杨氏双缝干涉原理图

杨氏双缝S1和S2是从同一个光波波面上分离出来的两个相干子光源，在它们的交叠区域中将出现干涉现象，原理图如图1所示.两缝中心的间距为d，双缝到接收屏之间的距离为D，且满足D＞＞d.波场中干涉加强的条件为

根据几何关系，

由以上两式得

因此只要知道k级干涉极大所对应的角度，就可以计算出波长λ.

图2 杨氏双缝干涉实验图

如图2所示布置实验仪器，将发射器和接收器的喇叭口正对，初始状态成一条直线分别安装在固定臂和活动臂上，活动臂刻线与180°刻度对齐.双缝板安装在中心平台的固定支架上，实验中双缝板的两条缝宽均为15mm，中间缝屏的宽度为50mm.发射器距离中心平台为35cm，接收器到中心平台的距离为 70cm（D=105cm，d=65mm，D＞10d）.打开电源，电流表置于“×1”档位，记录初始位置的电流值.缓慢转动接收器的活动支架，电流表上的数值每隔5°记录在表1中.

根据表1中的数据绘出图形如图3所示.由图可以看出，第一级干涉极大所对应的角度为θ=25°.根据（3）式，代入d和θ数值，可以计算出λ=3.03cm，与理论值3.00cm非常吻合，相对误差为1%.

表1 杨氏双缝干涉实验数据记录表

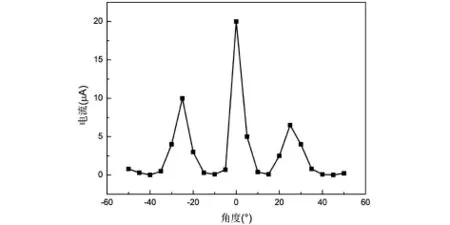
图3 杨氏双缝干涉强度与角度的关系

2.2 劳埃德镜[5,6]

图4 (a)劳埃德镜原理图 (b)微波光学实验仪中劳埃德镜示意图

如图4（a）所示，劳埃德镜为一反射镜.从狭缝射出的光S，一部分直接射到屏幕P上，另一部分掠射到反射镜M上，之后反射到达屏幕P上.由于反射光可看成是由虚光源S’发出的，那么S与S’可以看成构成一对相干光源.在屏幕上可以观察到明、暗相间的干涉条纹.

对于此仪器，如图4（b）所示，发射器和接收器距离转盘中心的距离相等，均为A，从发射器发出的微波一路直接到达接收器，另一路经反射镜反射后再到达接收器，两列波在交汇点处将发生干涉.实验中，反射板处于位置1的时候，干涉出现极大值；当它从位置1移到位置2的过程中，干涉条纹出现了N个极小值后再次达到极大值.由光程差可以得到：

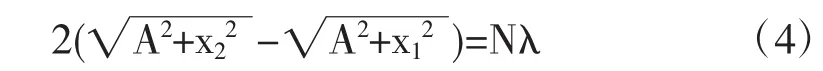
那么

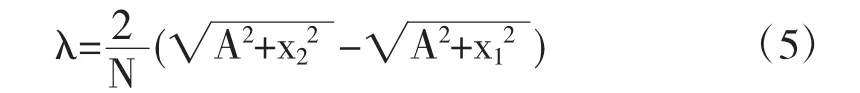
图5 劳埃德镜实验图

如图5所示布置实验仪器，将发射器和接收器处于同一直线上，分别安装在固定臂和活动臂上，且到中心平台的距离相等.反射板固定于移动支架上，其平面与发射器和接收器的直线平行.接通电源，电流表置于“×0.1”档位.在活动支架缓慢移动反射板的位置，当电流表出现一个极大值时，记录此时反射板的位置x1；当电流表出现N个极小值后再次出现极大值时，记录此时反射板的位置x2，把测量出来的数据记入表2中，重复测量三次.并计算微波波长及误差.

表2 劳埃德镜实验数据记录表

2.3 迈克尔逊干涉[5,6]

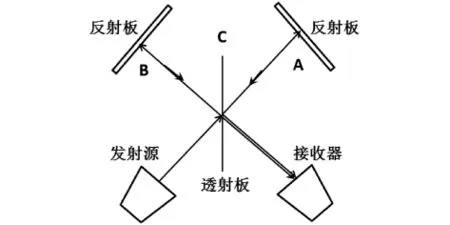
图6 微波光学实验仪中迈克尔逊干涉示意图

迈克尔逊干涉是将一列波分裂成反射和透射两列波，透射波再次反射后和反射波叠加形成干涉条纹.迈克尔逊干涉仪的结构如图6所示.C是透射板，A和B是反射板.从发射源发出的微波一路从C反射到B，然后经B反射后又回到C，最后透过C进入接收器；另一路分波经C透射后射到A，然后经A反射后再经C反射最后进入接收器.由于这两束波是相干波，在接收器相遇将会产生干涉现象.

若两列波同相位，那么接收器上将接收到干涉极大现象.这时移动其中的一块反射板（A或B），若两列波不再同相，那么接收器接收到的干涉将不再是极大值.若此反射板移过的距离为λ/2，波程将改变λ，接收器接收到的信号出现一次极小值后再次达到极大值.据此，我们可以通过改变反射板的位置来测量微波波长，得到的公式如下：

式(6)中Δd表示反射板移过的距离，N为接收到干涉极小值的次数.

图7 迈克尔逊干涉实验图

如图7布置实验仪器，透射板C与发射源、接收器及反射板支架都成45°关系.接通电源，使电流表置于“×0.1”档位.移动反射板A，当电流表读数最大时，记下A板位置x1.向外缓慢移动A板，当电流表读数出现10个极小值并再次达到极大值时停止，记录此时A板的位置刻度x2.所测数据记录在表3中，并计算微波波长及误差.

表3 迈克尔逊干涉实验数据记录表

2.4 法布里-珀罗干涉[7,8]

法布里-珀罗干涉是一种多光束干涉，主要由两块平面玻璃板构成.平面玻璃板相对的内表面很平，并且镀有高反射的膜.在两膜之间可以形成一个平行平面空气层.为了避开平面玻璃板外表面上反射所产生的干扰，两块板一般都稍微做成楔形.

图8 法布里-珀罗干涉原理图

如图8所示，设单色平行光S0以小角度θ入射到左板上，S0在两个之间来回多次反射和透射，分别形成一系列反射和透射光束.这一系列相互平行且有一定光程差的透射或反射光束经眼睛或透镜汇聚，在焦平面上将发生多光束干涉.令d代表两膜之间的距离，θ’为镀膜内表面的倾角，则相邻两透射光束的光程差为

而根据干涉产生极大的条件（1）式，两式结合得

实际使用法布里-珀罗干涉装置时，能在视场中形成干涉条纹的光线的入射角都很小，即cosθ'=1，那么

由此可得

其中Δd表示d的改变量，Δk表示在改变Δd时视场中移过的条纹数.

图9 法布里-珀罗干涉实验图

如图9所示布置实验仪器，两块透射板平行放置于活动支架上.接通电源，电流表置于“×0.1”档位.调节两板之间的距离，使电流表的读数达到最大，记下此时的距离d1.使右边透射板向远离左边透射板的方向移动，直到电流表读数出现10多个极小值并再次达到极大值时停止，记下经过极小值的次数Δk及此时两透射板之间的距离d2.数据记录在表4中，并计算微波波长及误差.

表4 法布里-珀罗干涉实验数据记录表

3 结束语

利用成都世纪中科仪器有限公司生产的ZKY-WB-2型微波光学综合实验仪模拟光的干涉实验，并进行了微波波长的测定.可以看出，测量结果较为准确.本实验仪提供了多种附件和实验方案选择，可以进行综合性、设计性和研究性实验.有助于学生更加深刻地理解光学实验的物理规律，为大学物理光学部分的理论和实验教学提供便利条件.