基于配置预测的能源结构优化研究——以美国四个州为例

张 彦，江治廷，姜浩华，周金明

（安徽工程大学 数理学院，安徽 芜湖 241000）

能源是人类生存之基，经济发展之本.建设生态文明是中华民族永续发展的千年大计，党的十九大报告中也明确指出：构建市场导向的绿色技术创新体系，发展绿色金融，壮大节能环保产业、清洁产业、清洁能源产业.2016年中国和美国政府批准了全球变暖对策新框架《巴黎协定》，标志着能源清洁低碳化利用已是当今全球发展的必然选择.目前，在温室效应导致全球变暖和能源紧缺问题日益严重的状况下，能源配置的结构优化以及提高可再生清洁能源的使用比例迫在眉睫.

近年来，关于能源配置与优化的研究亦集中于全球能源的结构性变革，于宏源[1]、王震[2]和何建坤[3]等主要基于全球能源大环境和《巴黎协定》等国际能源政策，对国际能源发展趋势进行研究，提出推进国际合作，推动能源体系的革命性变革，促进能源清洁低碳化转变的趋势和潮流已经不可逆转.其较全面地分析了全球能源结构性变革的趋势，但研究缺乏大量数据支撑.就能源预测而言，国内外学者以及研究机构采用了大量方法如：支持向量回归机技术[4]、灰度预测技术[5]和GA-SA算法技术[6]等.按预测方法的差异，预测可以分为回归预测法和时间序列预测法两大类，回归预测法则是研究变量与变量之间相互关系的一种数理统计的方法，应用回归分析从一个或几个自变量去预测因变量的值；时间序列预测法是一种考虑变量随时间发展变化规律并用该变量以往的统计资料建立数学模型做外推的预测方法.

鉴于此，本文研究能源配置优化与预测，在考虑能源结构性变革以及国际大背景下，提出典型相关分析法，结合TOPSIS评价模型对能源系统进行多因素分析，以保证能源配置最优化；综合考虑十大能源（生物质能、煤炭、水能、净进口电力、地热能、天然气、核能、石油、太阳能、风能）的历史发展趋势，结合时间序列预测法，研究能源未来的发展，以保证提出的政策建议有真实可靠的数据基础.

1 四州的能源配置情况

1.1 四州能源配置图

查找美国能源数据库[7]，将能源分为10种：生物质能、煤炭、水能、净进口电力、地热能、天然气、核能、石油、太阳能、风能.构建数据透视表，绘制出能源配置文件的堆积面积图如下1-4图所示.

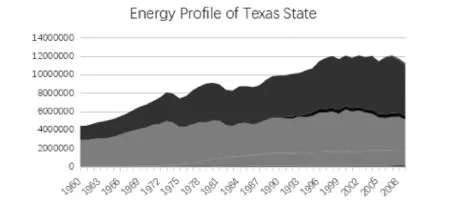
图1 德克萨斯州能源配置图

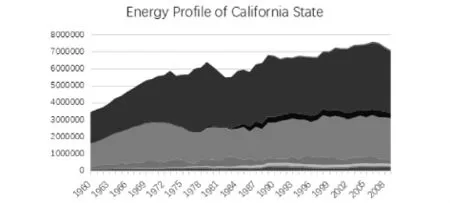
图2 加利福尼亚州能源配置图

图3 新墨西哥州能源配置图

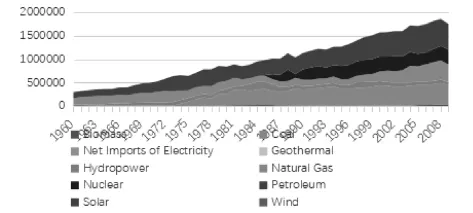
图4 亚利桑那州能源配置图

1.2 能源配置环境下的典型相关分析模型

描述四州能源配置的发展概况，建立典型相关分析模型，将地理、气候、经济、人口及行业因素与四州能源状况联系在一起.

1.2.1 地理、气候、经济、人口及行业因素的数据来源

地理气候因素数据，采取专家打分的方法根据其自身的地理环境优劣状况进行打分，如表1.

表1 地理和气候因素打分表

经济因素选取各个州的实际GDP（chained 2005 dollars）作为数据；人口数据采用各州的包含武装部队在内的常住人口；行业因素，分为五大类（运输部门，商业部门，电力部门，工业部门，住宅部门）用各部门总能耗作为数据.

1.2.2 典型相关分析模型的求解

通过软件进行典型相关[8,9]，以亚利桑那州为例，将其数据代入运行(参见表2).

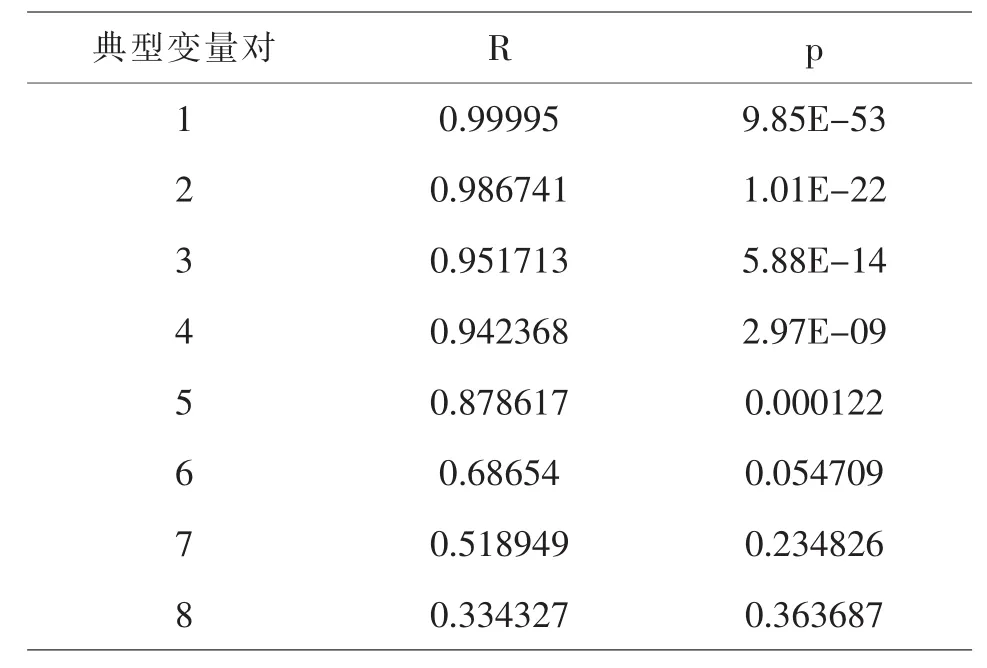
表2 典型相关分析数据

表3 标准化后的典型变量系数表

表4 标准化后的典型变量系数表

由表可知前五个典型变量对的p值小于0.05，故可认为前五对具有统计学意义，得到标准化后的典型变量系数（参见表3，表4）.第一对典型相关变量中，地理(x2)和气候(x3)与地热能(y4)和太阳能(y9)相关性较大.主要表现在地热能和太阳能与地理成正相关，与气候呈负相关.第二对典型相关变量中，人口(x1)与天然气(y6)相关性较大，主要表现在人口与天然气呈负相关.第三对典型相关变量中，经济(x4)和住宅部门(x9)与煤炭(y2)和核能(y7)有较大相关性，其表现在煤炭与经济呈正相关，与住宅部门呈负相关，核能与经济呈负相关，与住宅部门成正相关.第四对典型相关变量中，商业部门(x6)和电力部门(x7)与核电(y7)的相关性较大，其表现在核能与商业部门呈正相关，与电力部门呈负相关.第五对典型相关变量中，运输部门(x5)与生物质能(y1)和净电力(y3)进口相关性较大，表现在生物质能与净电力进口和运输部门呈负相关.

四个州在能耗总量上也呈现出不同的样貌.TX和CA的总能耗远远高于AZ和NM.由典型变量系数可知，能耗与GDP、人口成正比，故TX、AZ在GDP、人口上的优势转换为巨大的能耗.NM在核能利用上远远落后其他三个州，原因在于其地理位置条件差，地处沙漠，没有良好的水资源，无法满足核电站的建设条件.风能利用上TX表现优异，其原因在于，和地理一样，气候对能耗有促进作用.TX拥有温带气候和亚热带气候，风力资源丰富，条件得天独厚.CA在煤炭资源的消耗上远不及其他州，这离不开CA的行业结构.CA多为高科技产业，故对煤炭的消耗极少.四个州都表现出在生物能、太阳能、地热能利用上的缺失，这些能源受地理、气候影响较少，故可以在此方面做出更大的投入，使其更具发展潜力.

2 能源结构配置下的TOPSIS评价模型

结合加利福尼亚(CA)、亚利桑那州(AZ)、新墨西哥州(NM)和德克萨斯州(TX)四州的2009年能源配置数据，对数据进行处理，结合熵值法利用TOPSIS评价模型[10]对四州能源配置进行分析，得到最优能源配置结构.

2.1 TOPSIS模型的构建

(1)由熵值法确定权重，构建加权规范矩阵.为使评价结果更符合实际，根据熵的定义，m个州n个能源指标，则能源指标的熵为：

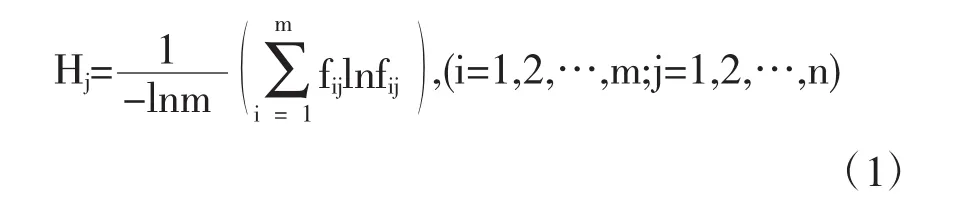
计算能源指标的熵权W：

构造加权规范阵C=(cij)m×n.由熵值法得到的各能源指标的权重向量为 W=(ω1,ω2,…,ωn)T，则

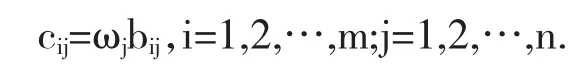
(2)确定理想最佳能源配置C*和理想最差能源配置C0.设理想最佳能源配置C*的第j个属性值为cj*，理想最差能源配置C0第j个属性值为cj0，则

理想最佳能源配置：

理想最差能源配置：

（3）计算各方案到理想最佳能源配置与理想最差能源配置的距离.各州能源配置方案di到理想最佳能源配置的距离：

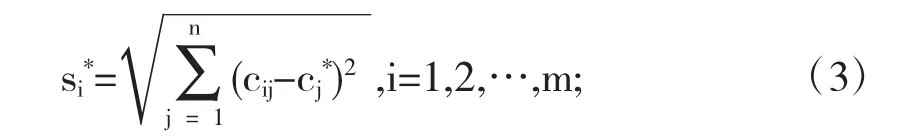
各州能源配置方案di到理想最差能源配置的距离：

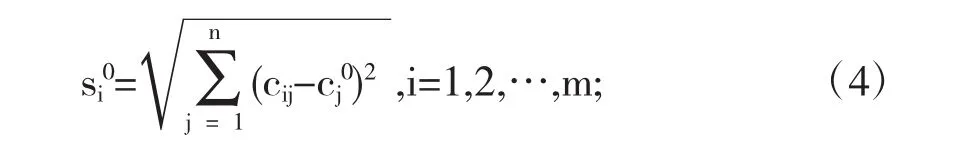
(4)计算各州能源概况的综合评价指数：

2.2 TOPSIS模型的求解

加利福尼亚(CA)、亚利桑那州(AZ)、新墨西哥州(NM)和德克萨斯州(TX)四州2009年能源数据表5所示：标准变换对数据预处理.将四个州在2009使用各项能源的数据转化为决策矩阵A=(aij)m×n，首先对数据进行预处理得到规范化矩阵B=(bij)m×n，其中:对清洁、可再生能源指标xj，令

表5 四州2009年能源配置数据

对其他能源指标xj，令

数据标准化处理结果（见表6）.

对标准化处理数据通过熵值法赋权重：

w=[0.01812,0.0256,0.0486,0.1344,0.1513,0.0812 0.1257,0.0289,0.1232]

表6 数据标准化处理指标值

表7 数据规范加权指标值

得到最佳能源配置解：

C*=[0.0661,0.0009,-0.0045,0.1299,0.1461,0.0052,0.0822,0.0011,0.1977,0.1149]

理想最差能源配置解：

C0=[0.0051,0.0284,0.0497,0.0003,0.0014,0.0736,0.0251,0.0018,0.0002]

计算各州能源概况综合评价指数如表8：

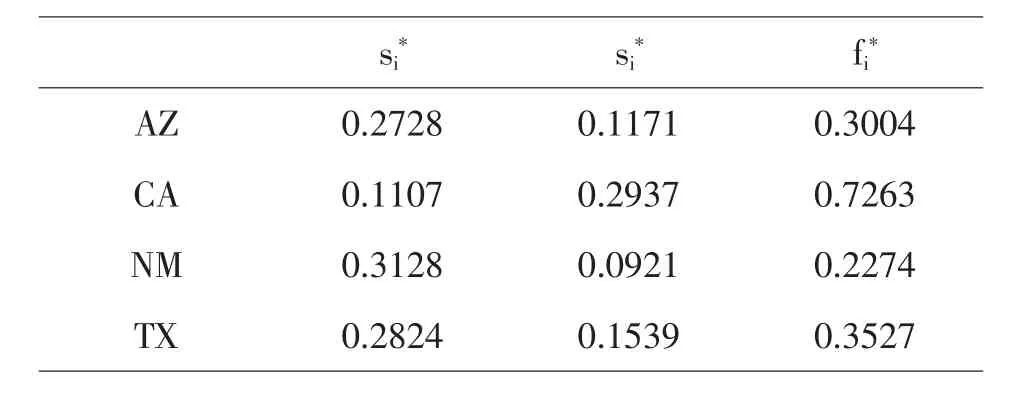
表8 各州综合指标值

由各州能源配置到最佳能源配置及最差能源配置的距离综合指标值得出：加利福尼亚2009使用清洁、可再生能源方面有“最佳”配置效果.

3 能源结构的配置预测——时间序列模型

3.1 基于能源配置预测的时间序列模型的构建

根据加利福尼亚(CA)、亚利桑那州(AZ)、新墨西哥州(NM)和德克萨斯州(TX)的历史能源发展情况，分析各州之间的异同，假定美国的有关能源政策没有任何变化，利用时间序列模型[11]，对各州能源概况进行预测.

(1)记原始序列数据为ai（t=1,2,…,n），作出时间序列模型的建模流程图（图5）

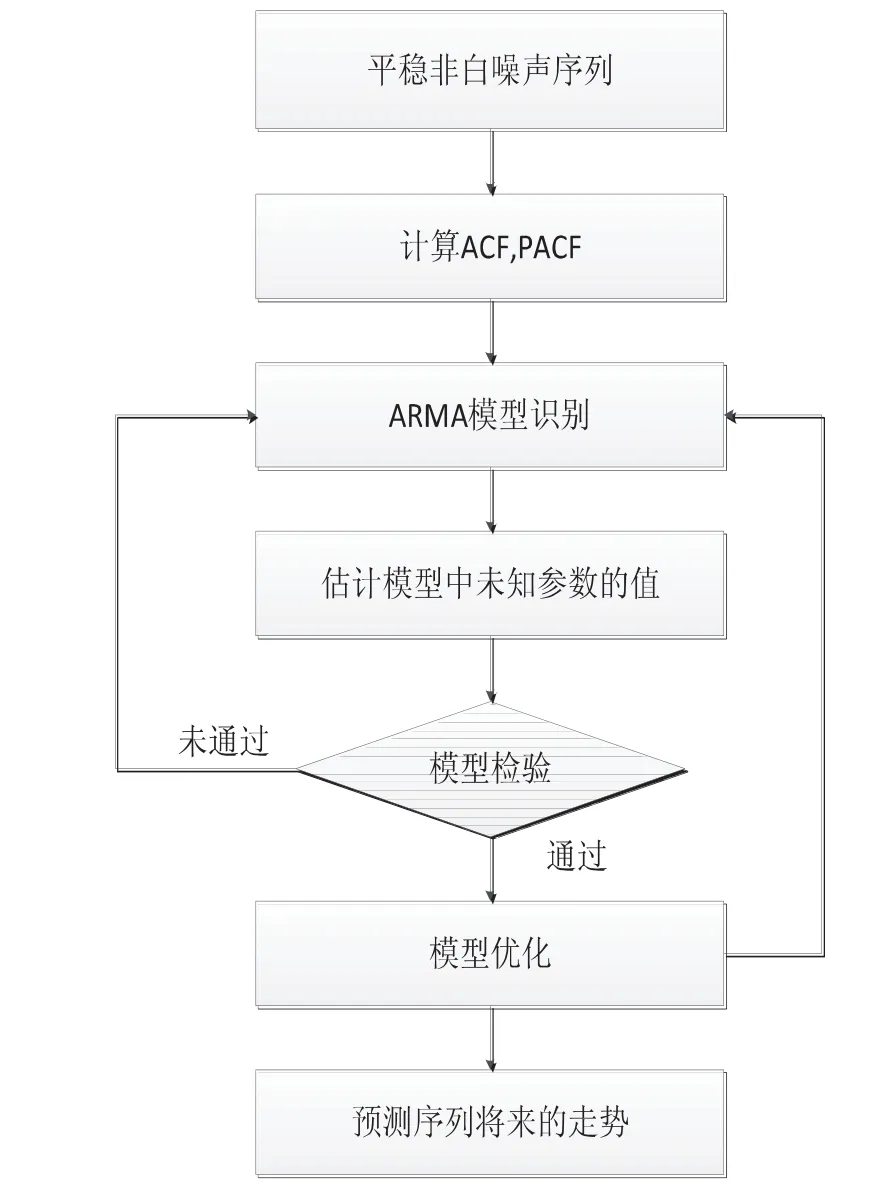
图5 时间序列模型的流程图

如图，建立时间序列模型时，要对原始序列进行平稳性和白噪声检验，若原始序列不平稳，可采用差分运算的方法将序列转化为平稳序列.

(2)模型中采用一阶差分运算：

(3)采取ARMA模型（自回归移动平均模型）进行建模，具体模型如下：

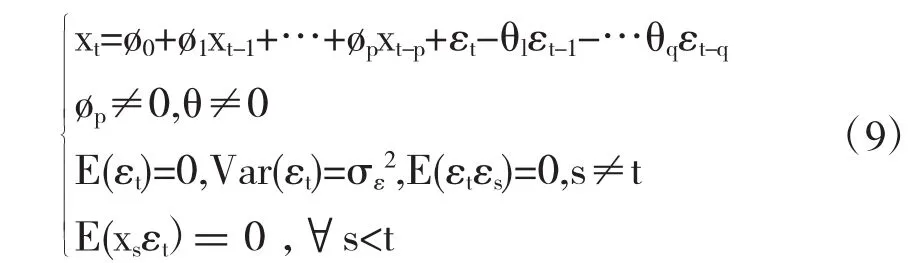
(4)模型的显著性检验，原假设和备则假设分别为：

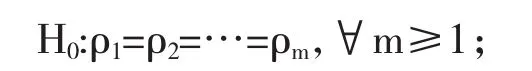
H1至少存在某个 ρk≠0，∀m≥1，k≤m；

其检验统计量为LB（Ljung-Box）为：

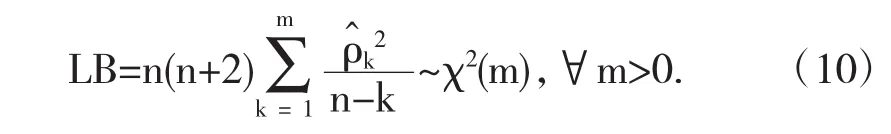
如果拒绝原假设，就说明残差序列中还残留着相关信息，拟合模型不显著.如果不能拒绝原假设，就认为拟合模型显著有效.

(5)参数的显著性检验，原假设和备则假设分别为：

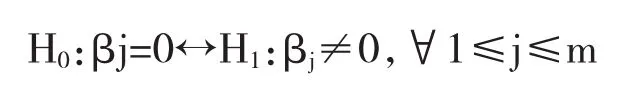
模型中进行线性拟合模型，对于参数进行最小二乘估计，构造用于检验未知参数显著性的t检验统计量：

当检验统计量的P值小于α时，拒绝原假设，认为该参数显著，否则不显著，需重新拟合模型.

3.2 基于能源配置预测的时间序列模型的求解

选取德克萨斯州(TX)的生物质能总消耗数据为例，其生物质能总消耗数据的时序图（图6）：

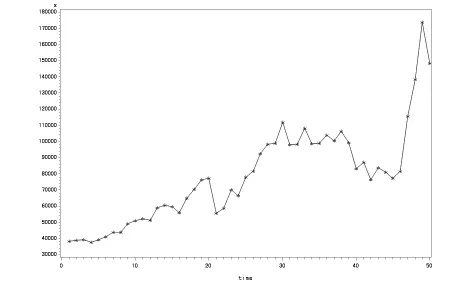
图6 德萨克斯州生物质能时序图

由图，该序列的生物质能的总能耗有一个明显随时间线性递增的趋势，所以该序列不具有平稳性.因此对序列进行一阶差分变化，获得一阶差分后序列的白噪声检验、时序图以及其对应的自相关图，偏自相关图如下（表 9）.由表可知：pr≤0.05，所以差分以后的序列为非白噪声序列.

由图7看出差分以后序列具有明显的平稳性，序列的自相关系数1阶截尾，偏自相关图1阶截尾，选取AR（1,1）模型（自回归模型）.

图7 差分后序列性质图

在进行回归时，对其待估参数进行最小二乘估 计，并对其残差进行检验，结果如下（表10）：

表10 残差序列白噪声检验

由表10，可以看出Pr≥0.05，说明残差序列为白噪声序列，说明模型可靠.最后预测出德克萨斯州(TX)的生物质能总消耗，在2025年和2050年德克萨斯州 (TX)的生物质能总消耗分别为：182822 Billion Btu，为：23616.28 Billion Btu.

3.3 各种能源预测数据的分析

图8 2025年四个州能源预测

图9 2050年四个州能源预测

对四个州的每一种能源分别利用时间序列模型进行预测，得到2025年和2050年每种能源的预测值，用图形进行解释：

由图8和图9，从时间的角度分析：2050年的各种能源使用量比2025年明显增多，且石油，煤炭，天然气等不可再生能源的用量稳定增多，风能，太阳能，地热能，生物质能等可再生能源的用量显著增多，电力的需求增加；从各个州的角度分析：在2025、2050年，德克萨斯州的能源利用最多，但是其水能，地热能利用量很少；其次为加利福尼亚州，该州在可再生能源与清洁能源使用的很好，且不可再生能源煤炭使用较少；对于亚利桑那州，能源利用较为均匀，可再生以及清洁能源使用较好，不可再生能源也有充分利用；对于新墨西哥州，其清洁可再生能源基本没有使用，主要使用的能源还是例如石油、天然气、煤炭这样的不可再生能源.

4 结束语

以上对美国四州的能源结构、配置以及未来能源发展趋势的研究，从美国能源消耗格局来看，美国消费者日益青睐清洁能源与可再生能源，如太阳能、风能、地热能以及天然气.而中国能源结构仍处于以煤炭为主的煤炭时代，在基于中国仍处于并将长期处于社会主义初级阶段的基本国情的基础上，借鉴美国能源配置概况，对中国提出以下建议：

(1)在发展新型可再生清洁能源的同时，中国应坚持以可持续发展为前提，加大对节约能源和提高能源利用的重视，促进中国成为能源节约型，环境友好型国家.

(2)当今世界能源利用正强调低碳环保，清洁可再生，并采取各种有效途径以减少不可再生能源、环境污染型能源的使用，积极发展利用新型能源.中国也应紧跟世界能源利用潮流，控制碳排放、将碳排放交易化并提高收费标准，对主要空气污染物实行严格的总量控制标准，将外在环境成本引入内部，使环境成本与财务成本相结合.

(3)随着世界各国不断发展与能源日益紧缺之间的矛盾逐步扩大，各国能源之间的竞争也将逐渐拉开序幕，中国应结合国情，用长远的眼光对待国内外能源局势，积极加强国内外技术交流与合作，吸取国外先进能源技术，并加大国内新能源创新创业扶持，提高国际间能源市场的竞争力和影响力，推进能源独立的战略政策.