基于定位法线的工件自由度判定方法及应用
王友利,张 铎,王晓慧
(太原科技大学 机械工程学院,山西 太原 0300024)
工件采用装夹法加工时,为了保证其在某一工序的加工精度要求,在加工前就必须使工件相对于刀具及机床处于准确位置,这就需要对工件进行定位,也就是对工件通过施加约束以限制工件的自由度,而工件自由度的约束在于通过与定位元件接触来实现。基于工件与定位元件接触关系,提出定位法线概念,根据定位法线数量及其之间的几何关系,建立自由度判定的几何定理及数学模型,通过数学模型来判定工件定位状态,使得传统自由度判定的定位原理转化为法线数量及几何关系的数学表达,更直观和简洁,为计算机辅助夹具设计中自由度的判定建立基础。
1 工件自由度判定的几何定理及其数学模型
1.1 定位法线及其自由度的判定几何定理
将工件与定位元件接触点的法线称为定位法线[1],简称法线,法线组成的平面为法平面。将定位元件与工件接触方式分为点接触、线接触和面接触[2],按照定位元件与工件定位要素的接触方式对其概括与分类,获得常用定位元件的定位法线数量和法线之间的几何关系,概括起来有以下几种:
(1)工件与定位元件为点接触,如定位元件为单个支承钉、挡销和削边销等,此时定位法线为工件与定位元件接触点处的法线,数量为1 条。特殊的点接触的还有工件采用顶尖定位锥孔,此时定位要素为锥孔,定位元件采用顶尖,接触方式可简化为3 个点的接触,定位法线互交且不共面,数量为3 条。
(2)工件与定位元件为线接触,如定位元件定位销、定位心轴、定位套和V 型块等。线可以由2 点来形成,一个圆可以由2 个点来确定,因此上述定位元件按照接触长度分为交点在轴心线上2 条相互垂直的法线,和交点在轴心线上相距一定距离的两对相互垂直的2 条定位法线。特殊的有采用支承板定位外圆,此时也为线接触,定位法线相互平行,数量为2 条。
(3)工件与定位元件为面接触,如支承板、阶梯轴的大端面等,定位法线则为平面上3 条相互平行但不共面的法线。
基于定位法线的数量及其几何关系可建立判定工件自由度的几何定理[2],简述如下。
(1)单法线:单条法线限制工件在其法线方向上的移动自由度。
(2)两法线相交:若工件的两条法线相交,则工件在法平面内沿法线方向的两个移动自由度被限制。
(3)两法线平行:若工件的两条法线平行,则工件沿法线方向移动自由度及绕法平面垂线方向的转动自由度被限制。
(4)三法线相交(不共面):若工件的三条法线相交于一点,则工件法平面内任意三个方向的移动自由度被限制。
(5)相交法线的等效:平面上的两条相交法线可等效为平面上任意两个方向互交的两条法线,限制该平面上任意两个方向的移动自由度。
工件上的定位法线所限制的自由度满足法线的集合定理,即一条法线限制一个自由度,限制自由度的数量等于法线的数量。根据六点定位原理,工件完全定位时法线的数量最多为6 条,法线数量超过6 条一定存在过定位情况。
过定位判断:三条法线相交且共面,则法线所在平面内的方向有一个移动自由度过定位;三条法线平行且共面,则沿法线方向移动自由度过定位。
1.2 基于几何定理的工件定位自由度数学模型
根据上述几何定理及其推导,建立笛卡尔坐标系,基于定位法线的工件定位几何定理的自由度数学模型见表1。

表1 基于定位法线的工件定位几何定理的自由度数学模型
2 实例应用
连杆工件加工大头孔的定位简图[3],图1 所示。工件的定位基面底面和小头孔均已加工,采用一个支承板和一个长销以及一个挡销定位,现分析工件该定位下的自由度。根据常用定位元件的定位法线的数量及其位置关系,将各定位法线在图中表示。支承板有3条不共面的平行法线,长销2 有4 条法线,挡销有1条法线,则一共有8 条定位法线,如主视图所示。工件完全定位时法线数量最多为6 条,所以该定位为过定位。法线FX1、FX2和FX3为不共面的三条平行法线,自由度模型

图1 连杆工件过定位分析简图


可看出其X^、Y^的自由度限制2 次,属于过定位。
根据上述自由度模型,要解决工件过定位有两种方式:
(1)第一种方式是将FY1和FY2两条平行法线中限制的X^和FX1、FX2和FX3不共面的三条平行法线中的限制的Y^消除掉,则需将FY1和FY2与FX1和FX2各去掉一条法线,也即将长销改为短销,如图2 所示。
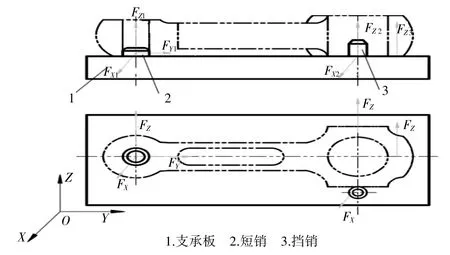
图2 连杆工件正确定位分析简图1



图3 连杆工件正确定位分析简图2
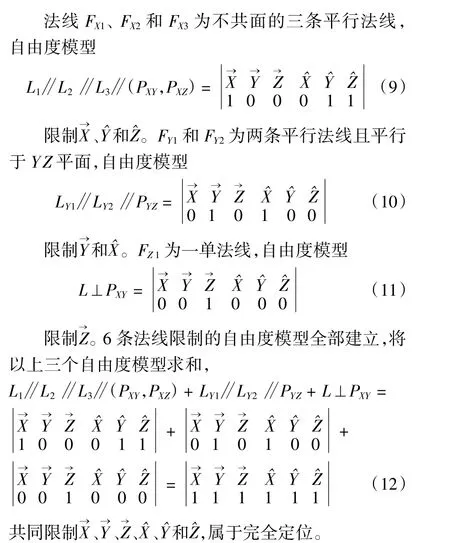
以上两种改进后的定位方式都可以使连杆工件完全定位,但从定位基面的稳定性选择来看,第一种方式的定位基面更大,相比较下第一种改进后的定位方式更好。
3 结语
基于定位法线的工件自由度判定的新方法,采用了简单直观的定位法线来表示,其几何关系和数学模型表达更直观简洁,特别适用于复杂零件和特殊零件的组合定位的分析判定以及不合理定位的改正。该自由度判定方法简单易学,可采用计算机辅助进行,为计算机辅助夹具设计中自由度的判定建立了基础。

