基于边缘结构模型的慢性乙型肝炎抗病毒疗效评估*

李伟南　林畅琪　郜艳晖　贾卫东　周舒冬△

【提　要】　目的　介绍边缘结构模型原理，并将该方法应用于具有时依性混杂变量的纵向数据中。方法　以慢性乙型肝炎(chronic hepatitis B,CHB)抗病毒治疗的初治患者随访研究为例，根据逆概率权重构建虚拟人群解决ALT和HBV DNA的时依性混杂，拟合边缘结构模型。结果　本研究所构建的边缘结构模型解决了在随访研究中时依性混杂对治疗组的影响，并有效地评估了各类CHB抗病毒药物的疗效。结论　边缘结构模型基于假设条件下能无偏地估计治疗/暴露组的效应，且弥补了传统生存分析方法在时依性混杂、删失和治疗转换问题上的不足。

分层分析和回归模型是常规的处理混杂的方法，但在药物流行病学研究中，往往会遇到一些和时间有关的混杂因素，即时依性混杂(time-dependent confounders)，这类混杂是影响治疗/暴露方式效应差异的一个重要因素。Robins等总结时依性混杂的特点包括随时间变化，影响后续治疗/暴露方式的选择，并且对结局也有影响；过去治疗/暴露方式对其也有影响[1]。可见时依性混杂不单是一个混杂变量，还是中间变量，如果使用常规的回归模型去调整混杂因素的影响，则其估计的效应是有偏的[2]。

在纵向数据的分析中，尤其是当存在治疗性转换、删失数据、时依性混杂因素的情况下，为了尽可能地无偏估计治疗/暴露方式的效应，可采用边缘结构模型，该方法由Robins在1997年首次提出[3]，目前国内对该方法的应用仍较少，而在国外已经得到了较为普遍的使用[4]，希望通过本文的研究能对今后该方法在国内的应用提供参考。

原理与方法

1.逆概率加权(inverse probability weighting，IPW)

边缘结构模型是基于虚拟人群(pseudo-population)对治疗/暴露方式进行效应估计，在虚拟人群中，每个人均存在于各治疗/暴露组，混杂因素无法起作用，得到的效应也就是真实的因果效应。虚拟人群的构建可以通过逆概率加权得到。

逆概率加权的公式如下：

(1)

其中，

t表示随访的次数，t=1,2,3,4,…;

Ak表示第k次随访时的治疗方式;

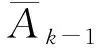
但是由公式(1)计算出来的逆概率权重容易出现极值，标准差大，易使样本量发生膨胀，从而与原样本相比更易拒绝零假设，且极值出现对结局会有异常影响[6]。因此，Robins等提出了稳定化权重(stabilized weights)[1]，通过保持与原人群一样的样本量，可降低极值,减小I类错误。

稳定化权重计算公式：

(2)

公式(2)是基于公式(1)的改进，被称为IPTW(inverse probability of treatment weighting)。

当然稳定化权重也有弊端，即加权后的虚拟人群没有被完全的调整，因为基线协变量被包含在了分子的权重中，所以在拟合边缘结构模型时，必须将这些协变量当作调节因素纳入模型中[7]。

当需要考虑删失时，可通过计算研究对象在不同协变量下不发生删失的条件概率，并以概率的倒数加权，使得人群具有平衡的删失比例[5]，(2)式可做如下改进：

(3)

2.权重的估计

逆概率权重的估计是基于合并logistic回归(pool logistic regression，PLR)模型，该方法要求数据结构以人时为单位，每个研究对象有多条观测记录。权重的具体计算以公式(3)为例，左分式分母部分的计算公式如下所示[1-2]：

(4)

右分式分母部分的计算公式如下所示：

θ1ktk+θ2kak+θ3klk

(5)

式(4)、(5)中，tk表示第k次随访的时间，分子的计算公式与分母类似，只需将lk替换为基线混杂因素v。

3.边缘结构模型(marginal structural model,MSM)

在对原人群进行加权处理得到虚拟人群后，该虚拟人群已不受时依性混杂因素、删失、治疗转换等情况的影响，此时进行治疗/暴露效应估计时能得到无偏的估计。

边缘结构模型的线性表达式如下所示[1,5,8]：

(6)

其中，

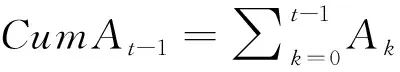
实例分析

1.资料来源

收集2008年1月至2015年12月到广州市第八人民医院进行抗病毒治疗的CHB初治患者，按照2015年版《慢性乙型肝炎防治指南》的诊断标准进行病例筛选。抗病毒治疗的药物包括恩替卡韦(entecavir，ETV)、替比夫定(telbivudine，LDT)、拉米夫定(lamivudine，LAM)、阿德福韦酯(adefovirdipivoxil，ADV)以及干扰素(interferon，IFN)。

2.研究方法

本研究为回顾性队列研究。随访起点为开始抗病毒治疗时间。收集患者的人口学资料(性别、年龄等)、每位患者自治疗开始后每6个月的血清HBV DNA、乙肝e抗原(HBeAg)、丙氨酸氨基转移酶(ALT)等，随访24个月。患者失访、四次随访后无发生结局事件或转为联合用药时定义为删失。结局事件为随访期间发生HBV DNA应答(<500 copies/ml)。

在抗病毒药物治疗过程中疗效主要受到ALT和血清HBV DNA两个时依性混杂因素的影响，即每一随访点的ALT和血清HBV DNA的水平可能影响当时抗病毒药物的选择，并且影响结局事件的发生；同时前一时间点的抗病毒药物治疗也会影响当前ALT和血清HBV DNA的水平[9-10]。因此本研究的基本思路如下所示：

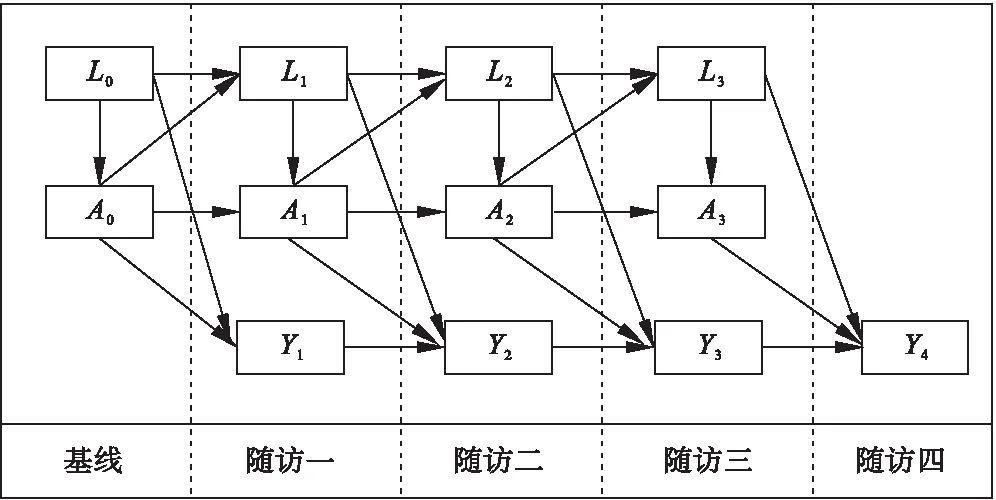
图1　抗病毒药物研究因果关联示意图

其中，

L0表示基线混杂包括：基线ALT、基线HBVDNA、年龄、性别、e抗原类型；L1表示时依性混杂包括：ALT、HBV DNA；Ai表示五种抗病毒药物；Y表示结局事件。

3.统计分析

本研究使用SAS 9.4对人口学资料进行统计学描述，使用proc logistic过程逐步进行逆概率权重的估计，使用proc genmod进行边缘结构模型的CHB拟合[11]。

4.结果

纳入研究的CHB患者共735人，CHB患者基线特征与用药模式的关系如表1所示。

表1　CHB患者的基线特征及用药模式

*：ALT正常值上限(≤40U/L)倍数，血清HBV DNA单位:log10copies/ml

以表1基线ALT为例介绍逆概率加权的原理，对五个抗病毒治疗组进行逆概率加权，以消除各治疗组在基线时ALT水平分布的差异，权重及加权后人群资料如表2所示。

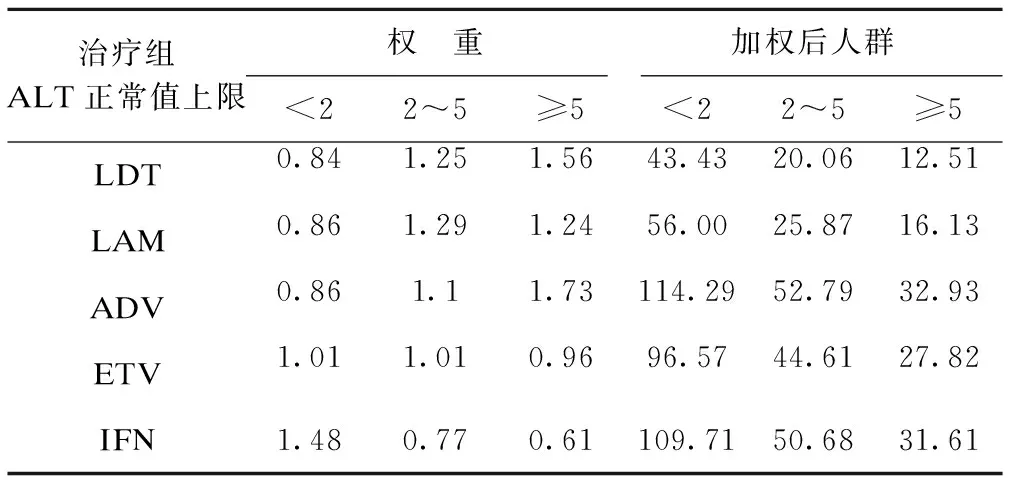
表2　权重及加权后虚拟人群

原人群通过逆概率加权后，混杂因素ALT在各治疗组间的分布达到平衡，表明ALT这个混杂因素已经被去除，所以对加权后人群进行分析，得到的结果是无偏的，在观察性研究中，逆概率加权可以被看成对数据的类随机化。同样在纵向数据的分析中，对研究对象的每条观测记录进行加权，从而解决随访过程中可能存在的时依性混杂、治疗转换和删失问题。

在735例患者的研究队列中，稳定化逆概率权重均值为0.98±0.38，最小值为0.11，最大值为3.49，权重在各随访点的分布如图2所示，随访点的权重均值均在1附近，未出现极值。

对加权后的原始人群进一步验证，判断不同治疗组与时依性混杂之间的关联，结果如表3所示。

表3显示了两个时依性混杂对抗病毒治疗组的“整体”作用，未经过逆概率加权的人群显示，不同抗病毒治疗组与血清学HBV DNA和ALT均存在关联。经过稳定化逆概率加权的虚拟人群显示，不同抗病毒治疗组与HBV DNA和ALT之间的关联均不存在。

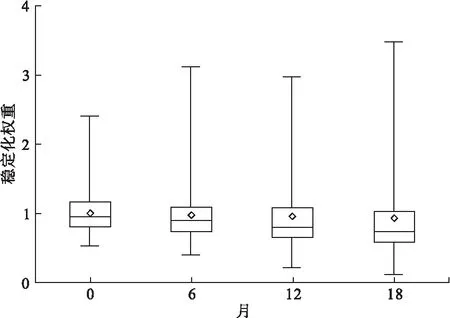
图2　各随访点权重分布图

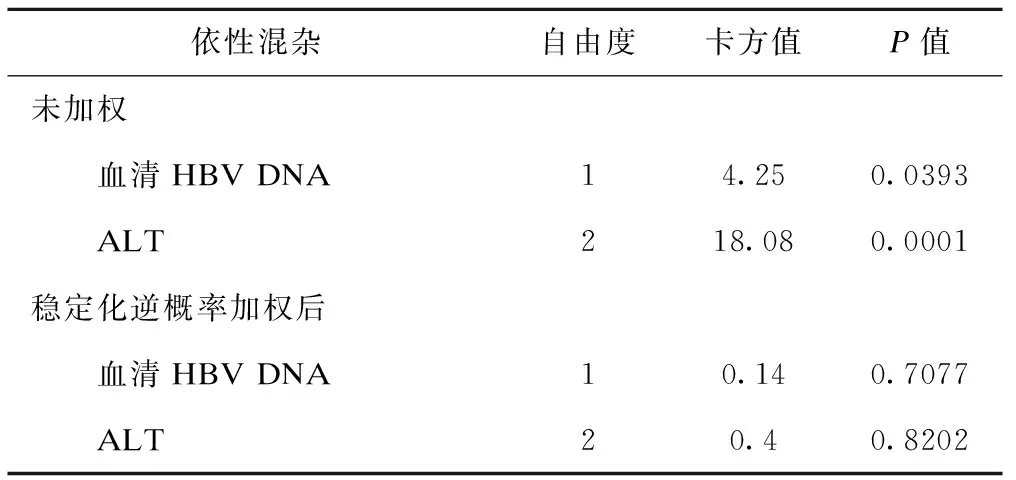
依性混杂自由度卡方值P值未加权 血清HBV DNA14.250.0393 ALT218.080.0001稳定化逆概率加权后 血清HBV DNA10.140.7077 ALT20.40.8202

假设在研究中不存在未观测到的混杂因素，对上述的虚拟人群构建边缘结构模型(MSM),设定不同抗病毒治疗组与HBV DNA应答结局的关系符合如下线性模型：

模型拟合结果如表4所示。表4结果显示，性别、年龄均无统计学意义；LAM、ADV、IFN对血清HBV DNA应答的疗效不及ETV，分别为ETV的0.61倍、0.62倍、0.45倍，e抗原阴性患者比阳性患者更易达到结局，差异有统计学意义(P<0.001)，在基线时ALT≥5×ULN(正常值上限)的患者比<2×ULN的患者更易实现HBV DNA应答，而基线时ALT为2～5×ULN的患者与<2×ULN的患者相比疗效差异无统计学意义。基线HBV DNA<6.0 log10 copies/ml的患者比≥6.0 log10 copies/ml的患者更易实现HBV DNA应答；随访二、随访三、随访四与随访一相比，提示随着时间的推移，HBV DNA应答率逐渐变缓。

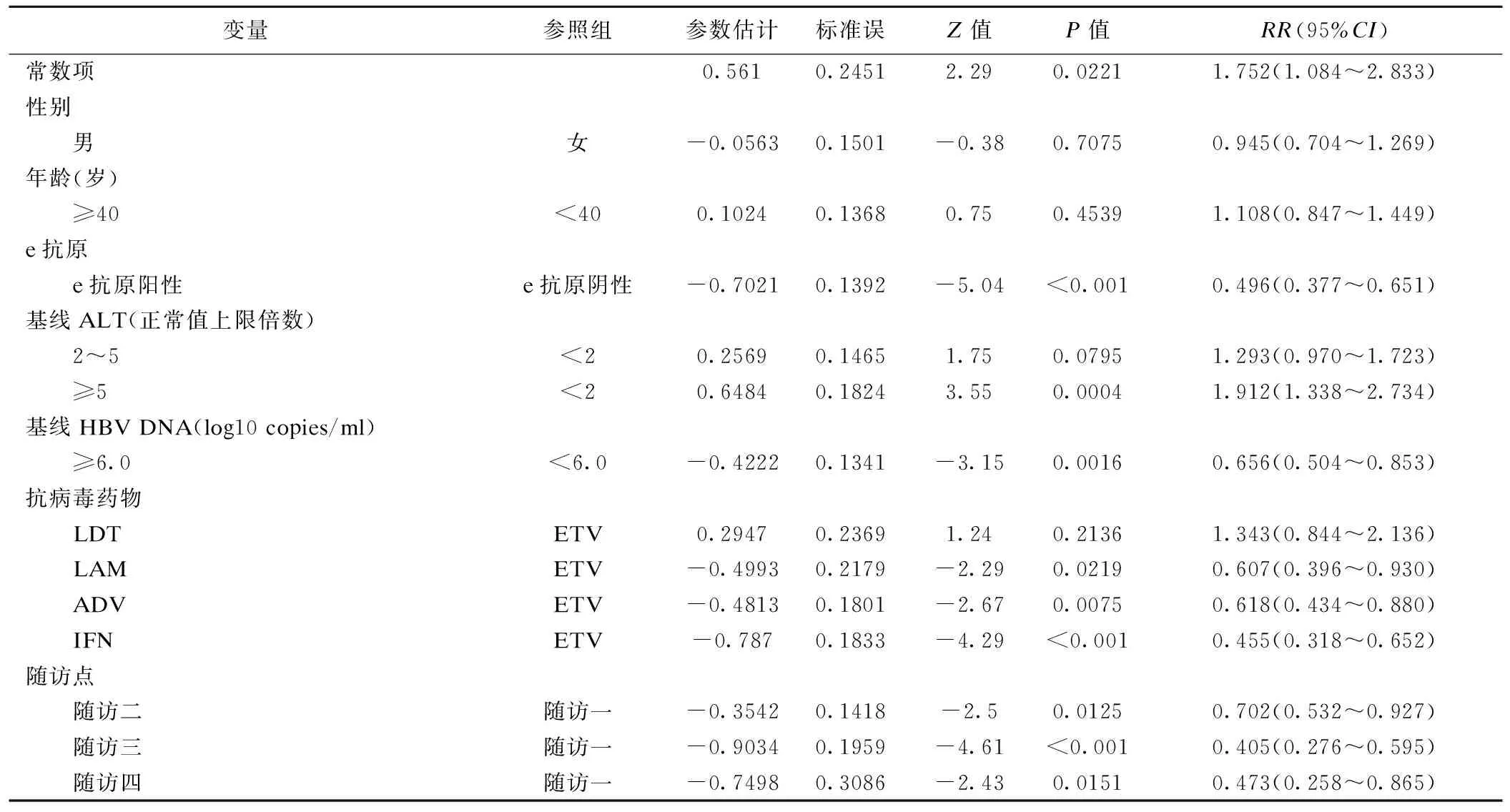
表4　边缘结构模型拟合结果

讨　　论

边缘结构模型与传统回归模型不同，他解决了时依性混杂因素的影响。以图1为例，当估计A0对Y2的效应时，如果回归模型加上L1，那么模型只能求出A0→Y2和L1→Y2的效应值，忽视了A0→L1→Y2的间接效应，这时会使得A0对Y2的估计有偏。而估计A1对Y2的效应时，L1对于A1是混杂因素，如果回归模型不加L1，那么A1→Y2的效应估计是有偏的，所以传统回归模型并不能很好地估计A的效应，而边缘结构模型通过加权消除了L1对A1的混杂作用，能通过拟合不加Li时依性混杂的模型来无偏估计A的累积效应[5]。

边缘结构模型的构建，基于3个关键的假设，包括(1)不存在未测量混杂，这个条件虽然难以进行验证，但也并不意味着纳入协变量越多越好，因为增加非混杂变量可能引入选择性偏倚；增加过多潜在混杂因素可能会导致有限样本偏倚，从而导致权重效应估计异常；将非混杂因素加入到权重模型中可能会降低效应估计的统计效率(即置信区间会变宽)。建议根据研究目的与专业背景，纳入可能的混杂因素。(2)非零假设，在协变量的不同水平下不同治疗组均有观测，即频数不等于0。如果非零假设不成立，那么权重会出现极值，导致估计出来的因果效应是有偏的。(3)模型的正确设定，主要包括治疗/暴露与混杂因素间的模

型设定；删失模型的设定；治疗/暴露组与结局效应间的结构模型设定[7,12]。和其他分析方法一样，如果上述假设无法满足则分析结果会产生偏倚。

在真实世界的疗效分析中，经常遇到治疗转换和删失，生存分析方法往往只是按删失处理，从而丢失了较多信息，而应用边缘结构模型对已加权的虚拟人群进行效应估计，考虑了时依性混杂的同时还包括过去的治疗史，因此该模型不单单解决时依性混杂的影响，而且通过改变数据中治疗转换的发生与协变量间的关联性，调整了治疗转换可能带来的偏倚。因此，在基于假设的前提下，本研究所构建的边缘结构模型在观察性研究中能对治疗/暴露组进行无偏的估计。