比例优势boosting算法在高维有序多分类数据分析中的应用*

哈尔滨医科大学卫生统计教研室(150081)　

张圆圆　赵薇薇　侯　艳　李　康△

【提　要】　目的　探讨比例优势boosting算法在高维组学多分类有序数据中变量筛选和分类预测的应用。方法　通过模拟实验和实例比较比例优势boosting算法和其他常用的多分类boosting算法在变量筛选和分类效果中的差异。结果　模拟实验表明，比例优势boosting算法的变量筛选效果，尤其在小样本情况下要明显优于其他方式，分类效果略优于其他方式；实例数据分析结果表明，比例优势boosting变量筛选效果要优于其他方式，在分类效果上略低于随机梯度boosting，但优于其他boosting方式。结论　比例优势boosting算法适用于高维有序多分类数据，具有实用价值。

临床实际应用中，癌症的分期对患者的治疗和预后具有很大的影响，随着检测技术的不断发展，高维组学数据(基因组学，蛋白质组学，代谢组学数据)大量涌现，利用组学数据寻找同癌症分期相关的标志物，预测癌症分期是临床上一个重要研究内容。由于癌症分期一般为多个类别，各类别间具有顺序性，属于有序多分类问题，且高维组学数据变量维数过高，常规方法无法处理。对于高维有序多分类数据的处理常使用随机森林(random forest，RF)[1]，多分类支持向量机(multi-class support vector machine，Multi-SVM)[2]等方法。近年来，人们开始重视boosting算法在多分类中的应用，这种算法通过加权组合多个基础分类模型来提高预测效果。然而，boosting和RF、Multi-SVM两种模型一样，都忽略了数据标签的有序信息。为此，针对高维有序数据有学者提出了比例优势boosting(P/O Boosting)模型[3]，该方法可以充分考虑数据标签的有序信息，在预测分类和变量筛选上更为合理，如错分相邻两类的损失与错分相隔较远两类的结果显然是不同的。本文将通过模拟实验比较有序和无序两种类型的boosting算法的分类预测和变量筛选的效果，并给出了应用实例。

方法和原理

1.常见多分类boosting

常见多分类boosting算法主要有Adaboost、SAMME、梯度boosting以及随机梯度boosting等四种方法[4]。

(1)Adaboost：基本思想是在迭代过程中，通过改变错分样本的权重建立一系列弱分类器，然后进行加权集成，最终得到一个强分类器。这种方法主要用于二分类标签数据，后将其扩展为多分类Adaboost.M1算法。

(2)SAMME算法：SAMME方法基于AdaBoost.M1算法，在损失函数误差项的计算中添加了log(K-1)惩罚项，降低了弱分类器的精度要求，自提出之后被视为boosting算法在多分类问题中的主要算法。

(3)梯度boosting：同Adaboost算法不同，梯度boosting并不关注错分样本的权重，而是在上一模型残差梯度减少的方向上建立新的模型，最终模型为多次迭代后的基础模型加权加和。

(4)随机梯度boosting：随机梯度boosting则在梯度boosting基础上增加了随机化参数，即在每次迭代过程中随机抽取一部分样本拟合分类模型。

2. 比例优势boosting

假定Y为K个有序类别的标签变量，预测变量表示为X=(X1，…，XP)，则比例优势模型为

(1)

其中，f(x)是基于预测变量X的可加函数模型，θk为模型的常数项，与各类的比例相关，限制 -∞<θ1<…<θk-1<θk=∞。对于给定模型，样本属于类别K的概率则为

(2)

比例优势Boosting模型则利用数据的有序信息，在损失函数的梯度方向上构建模型，即通过不断迭代时，计算基分类器的负向梯度，将其作为新的反应变量建立新的分类器。具体算法如下所示[3]：

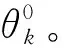
(2)进入循环m=m+1；

•计算模型损失函数L的负向梯度向量

(3)

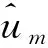
•更新当前函数估计值(v为预设步长)

(4)

•固定函数模型，通过最小化经验风险估计

(5)

直至M次后，循环结束；

(3)最终集成函数模型为

(6)

评价指标

1．分类效果评价

预测效果评价可以使用分类正确率和ROC曲线下面积(AUC)，泛化的多分类AUC计算如下[5]：

(7)

这两种指标主要用于二分类预测模型评价，也可用于多分类预测模型，但对于有序多分类来说，样本被错分至相邻类别所付出的代价要比错分至较远类别的代价小，为此，本文给出一种新的评价指标—校正评分。

校正评分通过对样本错分至不同的类别时，依据类别的远近进行惩罚,对分类器的分类效果做出综合评价，惩罚函数如下

S=e-λd，d≥0

(8)

其中d为预测类别和真实类别之间的距离，λ为衰减系数，可根据实际问题进行自定义，本文选取λ=1。

2．变量筛选评价

为考察不同方式筛选变量的效果，通过重抽样技术选择训练样本进行建模，每次建模过程中将各变量按照变量的重要性进行排序，获得各变量的秩次，取重复r次各变量的平均秩次作为变量的最终排序。根据模拟的差异变量个数m选择对应前m个变量作为“差异变量”，然后计算所筛选变量的正确率。

模拟实验

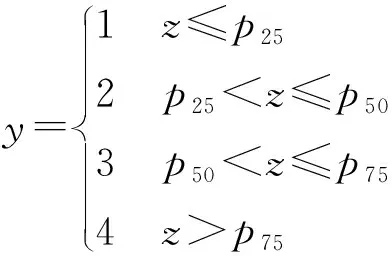
模拟四分类有序数据：设定6个差异变量x～N(0，1)， 指定中间变量z，且

(9)

根据z的取值范围，以P25，P50，P75等百分位数为界限定义有序四分类，如下所示

为在不同的情况下分别比较AdaBoost.M1、SAMME、GBM、SGBT以及P/O boosting五种方法在测试集的变量筛选效果和分类效果。分别设定N={240，120，40}三种不同样本量的模拟数据作为训练集建模，并对1000例的外部测试集进行预测，重复次数r=50。在此基础上，通过调整各类别百分位数界限，以N=40为例，各类别的界限范围分别为z≤P10，P30≤z≤P40，P60≤z≤P70以及z≥P90，比较类别间差异增大时对五种方法的影响。评价分类效果使用正确率(accuracy)、ROC曲线下面积(AUC)和校正得分(score)统计量。

模拟结果显示，在三种不同样本量下，使用P/O Boosting方法筛选变量的正确率分别为100%、100%、66.67%，明显优于其他四种方法(表1)。固定样本量，类间差异增大时，各方法变量筛选结果的差异减少，但P/O Boosting仍能获得不弱于其他方法的筛选结果。由图1可以看出，在分类效果上，P/O Boosting均略优于其他方法。上述模拟实验结果表明,P/O Boosting方法的主要优势在于筛选变量上有更好的结果，尤其是小样本小差异情况下。

表1　不同情况下变量筛选结果比较

#单元格中分别为准确率(正确个数)，N*为类间差异增大时的结果

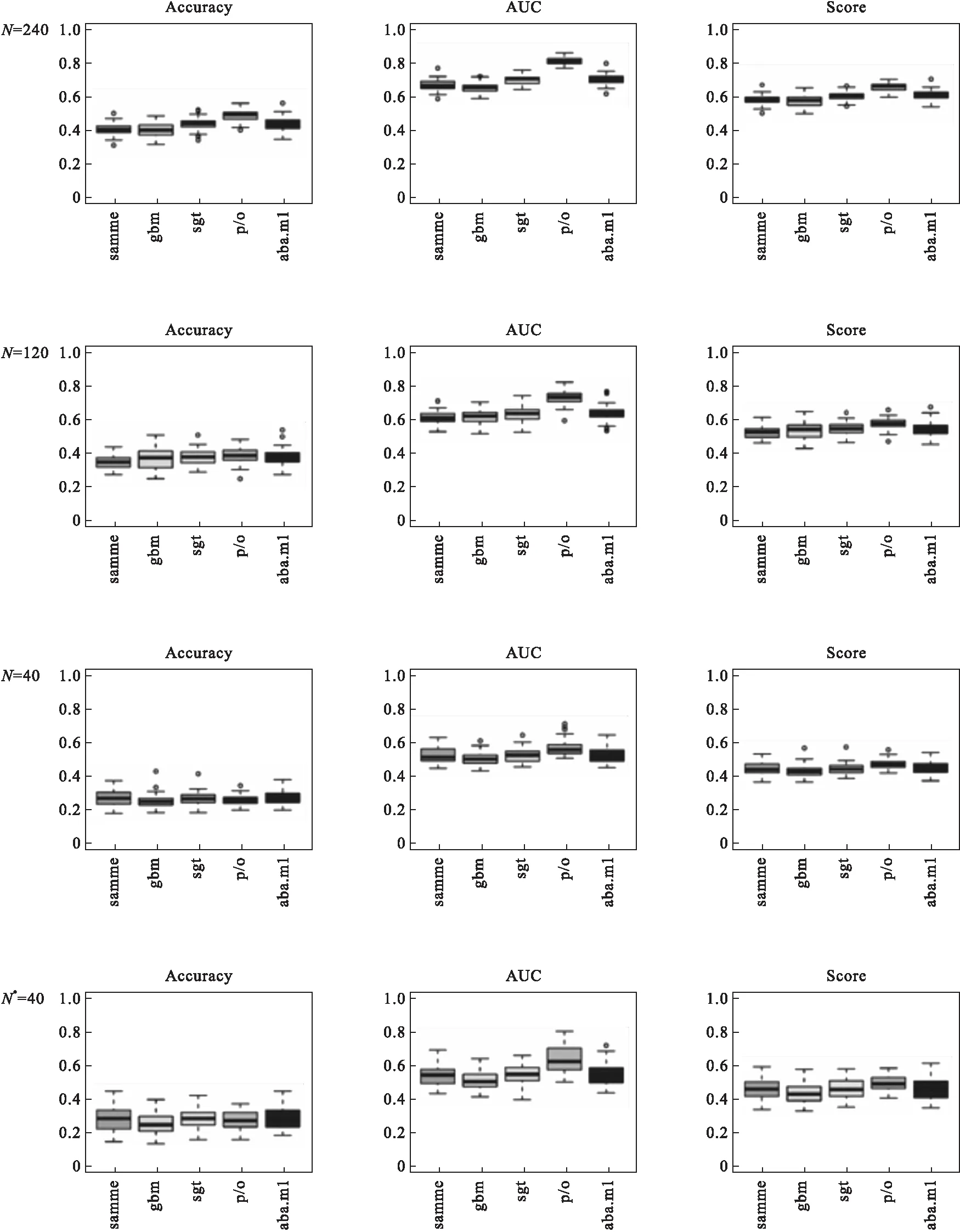
图1　不同情况下五种分类方法的比较

实例应用

为进一步在实际中验证以上五种boosting算法的对比结果，选用TCGA中结直肠癌(COAD)的mRNA数据，筛选同结直肠癌分期相关的变量，预测患者的疾病分期。该数据总共包括358例样本，20530个预测变量，经过单变量分析(非参数秩和检验，阈值为0.01)初筛获得1373个变量，对初筛后的数据进行分析。随机抽取100例作为训练集，其余作为测试集进行建模预测，每次对变量重要性评分进行排秩获得变量在该次建模过程中的秩次，重复以上步骤r(r=50)次后，计算平均秩次并重新排列，选取前m个变量作为各方法的差异变量，然后与所有358例样本建模筛选的前m个变量相比较，观察两者的重合率，最后通过查阅文献，确定五种方法所筛选变量中当前已有文献报道同癌症相关的基因所占的比例。

分析结果显示，五种方法中，当m=20时，P/O Boosting的重合率为50%，文献报道率为80%；当m=50时，P/O Boosting的重合率为48%，文献报道率为76%，均表示该方法可靠性较高(表2)。从生物学上看，多数基因能够得到较好的解释，例如，筛选出的SCEL基因通过激活β-连环蛋白及其下游的原癌基因增强wnt信号通路，并通过SCEL-β-连环蛋白-E-钙粘蛋白轴激活间充质—上皮细胞转化(MET)过程，降低癌细胞的迁移和入侵[6]。再例如，筛选出的EFNB2可能是功能获得性突变P53的靶基因，通过P53/ ephrin-B2轴参与结直肠癌中的上皮细胞-间充质转化(EMT)过程，降低患者的化疗敏感性[7]。从分类效果上看，五种方法在各分类指标中结果相差不大，P/O Boosting的AUC值略优于其他方法(图2)。

表2　COAD数据不同样本下各方式变量筛选效果比较

*重合率为100个样本建模同全部样本建模筛选出的变量重合比例

图2　五种方法COAD数据分类结果

讨　　论

P/O Boosting是专门针对高维有序分类数据分析的一种方法，同常规的无序多分类模型相比，这种模型能够考虑并利用数据的有序信息，其主要特点是在小样本条件下，依然能够较好地筛选出差异变量，可以为后续的机制研究以及临床实际应用提供有益的信息。

P/O Boosting模型有一个重要的假定，即任意两个不同累积有序类别的比数比相同，如果实际数据不满足这一假定，对变量筛选影响不大，但可能会影响分类的效果，因此这种方法更适合于变量筛选。

有序和无序分类的主要差别是可以将相邻类进行不断合并，从而使建立的模型更为稳定；另一差别是错分的损失与相隔距离有关，P/O Boosting模型在建模时并未对其加权，因此使用校正评分统计量进行评价时并未达到预期的效果，如何将该统计量应用于模型的建立过程中，需要进一步研究。

本研究给出的P/O Boosting算法的基础分类器选择的是树模型，适合多种复杂的情况，实际中也可以选择其他类型的分类器，如样条函数等，不同基础分类器得到的结果会略有差别。