基于LASSO的FDR控制方法及其在高维数据生存分析中的应用*
许树红 董晓强 陶 然 高 雪 高 倩 虞明星 王 彤△
【提 要】 目的 基于LASSO-Cox模型探索交叉验证(cross validation)、pcvl法(penalized cross-validated log-likelihood)、EBIC准则(extended bayesian information criterion)、平稳选择(stability selection)四种方法在控制FDR(false discovery rate)方面的表现及其变量选择效果。方法 通过模拟研究评价各方法在不同删失比例、自变量间不同相关程度以及回归系数的不同稀疏水平下的FDR和PSR(positive select rate),并从GEO上下载DLBCL数据进行基因与预后间的关联分析。结果 模拟结果表明,在不同删失比例、自变量相关程度和稀疏水平的情况下,平稳选择法控制FDR的能力都优于其他方法且其变量选择效能也较高。EBIC准则在相关程度低、自变量较稀疏时表现较好,当样本量较小时结果较保守。pcvl法虽然不容易漏掉有效应的变量,但其FDR仍较高。实例结果显示,EBIC准则只选出1个基因,平稳选择法选出的基因中大部分有统计学意义且与其他方法的结果重合度高。结论 在基于LASSO-Cox模型的高维数据生存分析中平稳选择法能较好地控制FDR且其变量选择效能也较高。
LASSO(least absolute shrinkage and selection operator)作为一种常用的惩罚类方法,在GWAS研究、测序数据分析中应用广泛且发展迅速,其中心思想是将模型系数的绝对值函数作为惩罚项对模型中变量的系数进行压缩,使得一些弱效应变量的系数变小,甚至被压缩为0,以提供一个稀疏解[1]。LASSO类方法通过直接估计不为零的回归系数来实现变量选择,它不同于经典的逐步回归,并没有采用假设检验的步骤,并且其变量选择和参数估计的结果在很大程度上受调整参数的影响,然而调整参数的传统选择方法如交叉验证法和信息准则法,在选择调整参数时主要考虑模型的拟合以及模型的复杂程度,亦未考虑Ⅰ类错误估计和控制问题。目前已有研究者指出LASSO类方法存在较高的假阳性问题[2-3],因此,如何在控制或降低假阳性的前提下,选择合适的调整参数从而选出正确的模型尤为重要。
目前已有一些研究在多重校正以及LASSO类方法的基础上,发展了一些控制Ⅰ类错误同时筛选出正确变量的方法[4]。FDR作为测序数据多重比较领域中控制Ⅰ类错误的常用指标,由Benjamini& Hochberg在1995年提出,指拒绝的假设检验结果中Ⅰ类错误所占比例的期望,在整体上控制Ⅰ类错误的同时能筛出更多有意义的基因[5]。本文将基于LASSO-Cox模型,通过模拟和实例研究比较交叉验证法、pcvl法、EBIC准则和平稳选择法四种调整参数选择方法在控制FDR方面的表现以及在高维数据生存分析应用中的优劣。
原理与方法
LASSO-Cox模型的最大化目标函数为:
(1)
其中p表示协变量的维数,β=(β1,β2,…,βp)T为各协变量对应的回归系数,l(β)为Cox模型的对数偏似然函数,λ>0为调整参数。调整参数λ的大小影响着模型的复杂程度和收敛速度,λ值过大可能会使最终的模型中协变量个数过少,导致重要的变量被遗漏,反之,λ值若过小可能会使最终的模型中协变量个数过多,使得模型包含很多噪声变量,导致结果中FDR过高。本课题组前期研究中已对基于LASSO的Ⅰ类错误控制方法的基本原理进行了详细阐述[4],本文对交叉验证法(cross validation,CV)、pcvl法(penalized cross-validated log-likelihood)、EBIC准则(extended bayesian information criterion)、平稳选择法(stability selection)的原理进行简单介绍。
1.交叉验证
目前最常用的交叉验证是K折交叉验证(K-fold cross-validation),K为整数,1≤K≤n,通常取5或者10。该方法利用训练集来建立模型并求得回归参数估计值,然后用该回归参数估计值来预测验证集。对于对数偏似然函数,其目标函数为:
(2)

2.pcvl
Ternès[6]针对传统交叉验证法容易出现过度拟合这一问题提出pcvl法,公式如下:
pcvl(λ)=cvl(λ)-pen(λ)
(3)
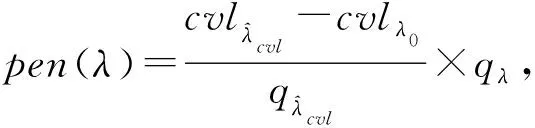
“体育是人的类存在的主体象征”[11],是人类主体本性需求下的产物,是本体体验与身体经验的结合,体育不仅是肉体强蛮的塑造之法,同时也是主体自由的解放之径。体育行为以对生命的养护为最终的实践目的,以主体的自由为最高的价值旨归,见证人类个体自我造就的每一时刻。以铜为镜,可以正衣冠;以史为镜,可以知兴替;以人为镜,可以明得失。体育相当于反观人自身的明镜,在体育竞赛中反观自我的品性,在体育训练中反观肉体的健康,在体育游戏中反观主体的自由。在体育的实践行为当中认识自我,发挥自身的优点,摒弃自身的不足,避免自身的异化。
(4)
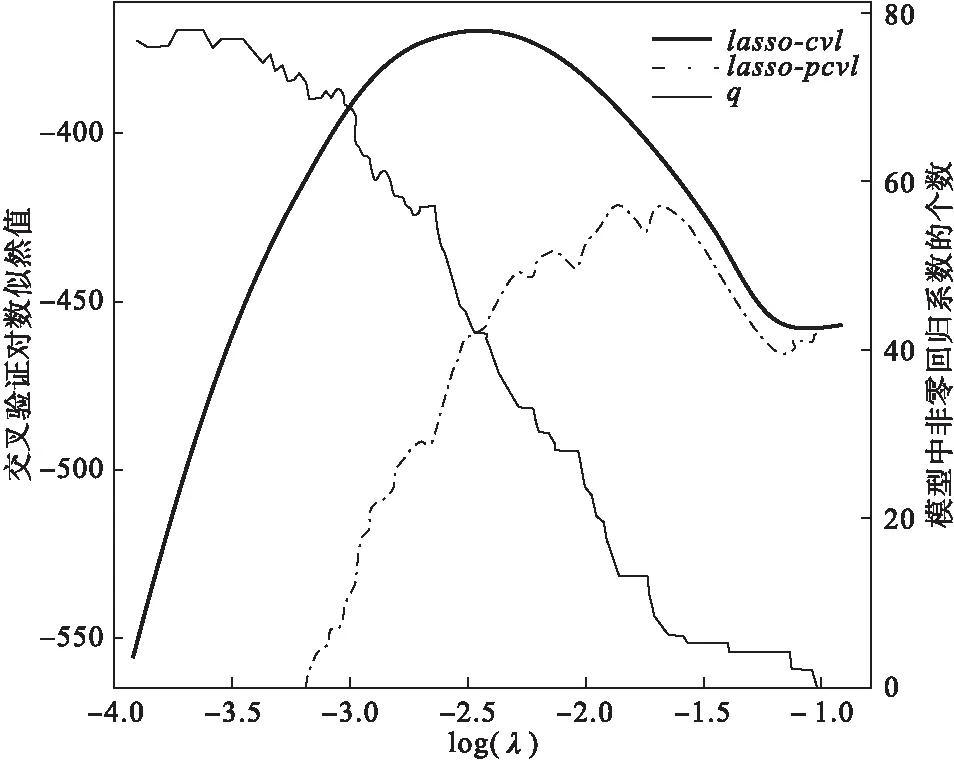
图1 cvl(λ)和pcvl(λ)以及模型中非零自变量个数随λ变化趋势图(n=100,p=1000,q=6,L=3时的模拟结果)
3.EBIC准则

(5)
当γ=0时,EBIC准则等于传统的BIC准则;当γ=1时,EBIC准则与mBIC准则类似。γ的取值大小影响着EBIC准则的选择一致性。Luo和Chen[8]基于线性模型对EBIC准则的选择一致性进行了深入的探讨。
4.平稳选择法
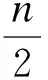
(6)
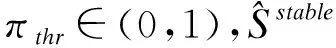
模拟试验
1.模拟试验设置
参考Luo、Song和Fan 等的模拟情形[13-15],模拟试验中自变量个数p=1000,样本量n=(100,120,140,160,180,200),模拟次数B=100。
模拟方案一:探索生存数据删失比例的不同和自变量间的相关程度不同对调整参数选择方法的影响,具体设置如下:
(7)
(8)
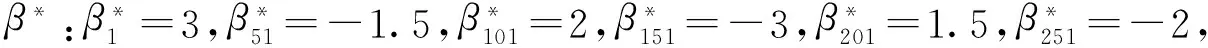
(3)删失时间是由均数为Uexp(-xβ)的指数分布产生,其中U是[1,L]上的均匀分布,不同的L值对应的删失比例不同,设置L=(2,3,4,5)。
模拟方案二:研究自变量的不同稀疏情况对调整参数选择方法的影响,具体设置如下:
(1)自变量服从均数为0的正态分布,自变量间相关结构与模拟方案一的区组相关结构相同。

(3)删失时间的指数分布中L=3。
2.模拟试验分析与评价
利用R 3.3.2软件中glmnet package建立LASSO-Cox模型,分别采用CV法、pcvl法、EBIC准则、平稳选择法进行调整参数的选择和变量筛选。利用cv.glmnet函数进行10折交叉验证分析。EBICγ1准则中γ取值为1,EBICγ2准则中γ取值略大于1-lnn/2lnp(在其基础上向上取整)。pcvl法由于还没有R软件包可实现,本次研究主要参考Ternès,Rotolo 和 Michiels提供的R程序[6]。利用lol package进行平稳选择,平稳选择的重复抽样次数设为100,截断点πthr取0.6。
评价指标主要为错误发现率(FDR)和PSR(positive select rate)。FDR作为变量选择的假阳性指标。PSR作为变量选择效能指标,用来评价模型发现确实存在的有效应变量的能力。FDR和PSR定义如下:
FDR=FP/(TP+FP)
(9)
PSR=TP/(TP+FN)
(10)
其中FP(false positive)表示在模拟试验的真实模型中回归系数为零,但估计的回归系数是非零的个数;TP(true positive)表示在模拟试验的真实模型中系数是非零,估计的结果也是非零的个数;FN(false negative)表示在模拟试验的真实模型中回归系数为非零,但估计的结果为零的个数。FDR越接近0、PSR越接近1,说明该调整参数选择方法越好。
3.模拟试验结果
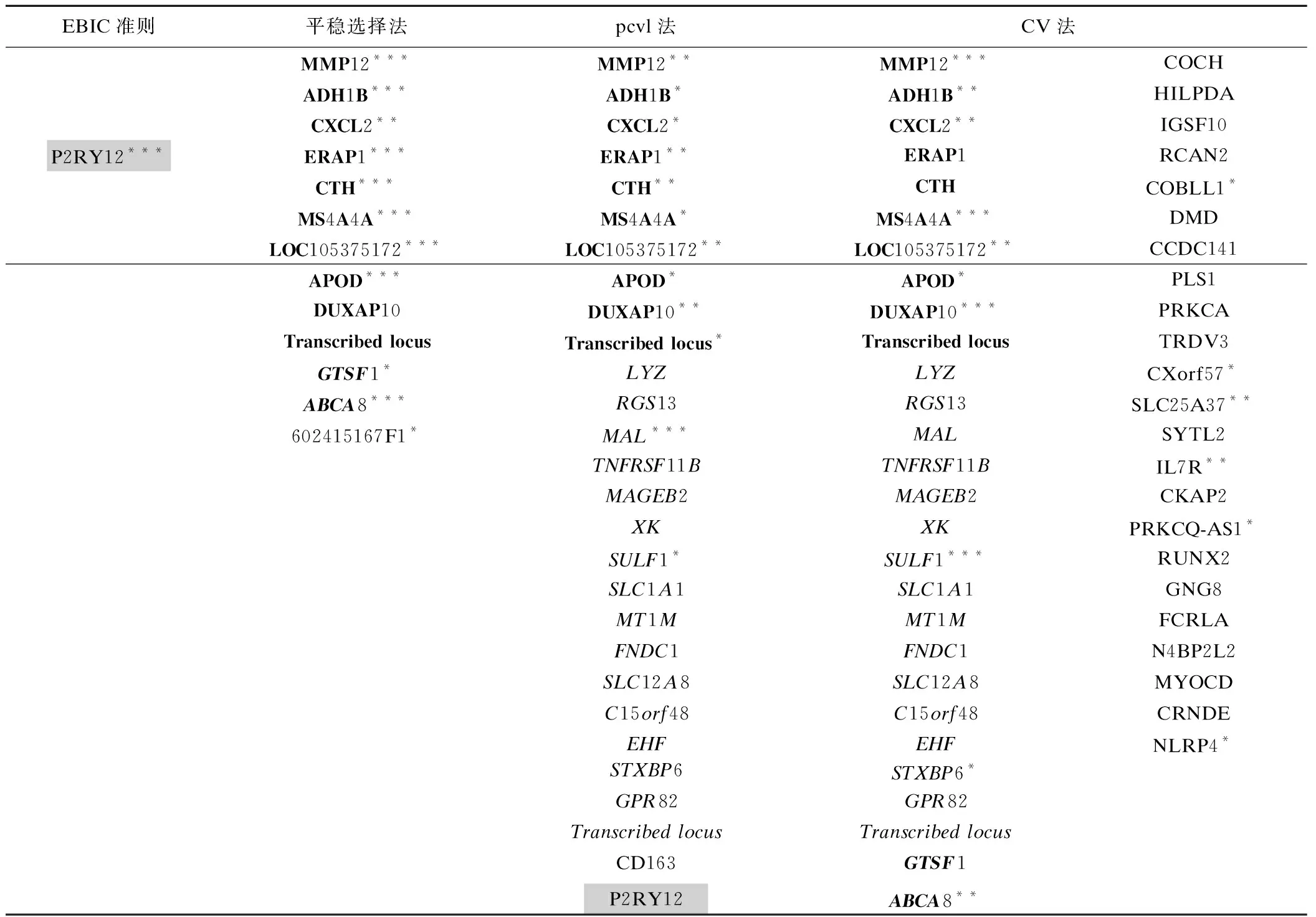
(1)如图2和图3,在样本量、删失比例、相关系数均一定的情况下,各方法的FDR从低到高依次为:平稳选择法≤EBICγ1准则 (2)如图4和图5,在样本量、自变量间相关系数和稀疏水平均一定时,各方法的FDR相比较结果以及PSR相比较结果与方案一的结果一致。随着真实非零自变量个数的增多即稀疏水平的降低,平稳选择法的FDR基本保持不变,pcvl法的FDR略升高且与CV法之间的差距逐渐减小,EBIC准则对稀疏水平的变化比较敏感,其结果波动较大;在样本量较小且真实非零自变量个数增多的情况下,各方法的PSR值均出现不同程度的降低,平稳选择法的PSR值始终高于EBIC准则。在样本量较大的情况下,随着真实非零自变量个数的增多,CV法、pcvl法和平稳选择法的PSR值基本保持不变且接近于1。 图2 不同删失比例和相关情况下模型变量选择的FDR(100次模拟的平均值) 图3 不同删失比例和相关情况下模型变量选择的PSR(100次模拟的平均值) (1)这些基因之间存在比较高的相关关系,每个变量与其他变量间的最大相关系数的平均值是0.810。 (2)上述方法选出与预后有关的基因数分别有51、28、13、1个,其中EBICr1准则和EBICr2准则结果一致。分别以各方法选出的基因为协变量,拟合Cox比例风险模型,得到的模型拟合结果如表1所示:平稳选择法选出的13个基因中有11个基因具有统计学意义,且与CV法相同的基因有12个,与pcvl法相同的基因有10个;pcvl法选出的28个基因中12个有统计学意义,与CV法相同的基因有26个,与EBIC准则相同的基因有1个。CV法选出的51个基因中只有16个基因具有统计学意义。其中MMP12、CXCL2、P2RY12、MAL基因已有文献报道与DLBCL 的预后和疾病进展有关[17-21]。值得注意的是有文献报道CD163基因与DLBCL预后有关[22],但只有pcvl法选出了CD163。实例结果表明CV法选出变量很多且大部分无统计学意义。pcvl法一定程度上减少了假阳性,且不容易漏掉有效应的自变量,但选出的变量仍比较多。CV法、pcvl法选出的有统计学意义的基因大部分被平稳选择法选出,且占后者结果的绝大部分,说明平稳选择法选出的自变量假阳性很低,且与其他方法结果重合度高。EBIC准则结果则过于保守。 图4 自变量不同稀疏水平下模型变量选择的FDR(100次模拟的平均值) 模拟研究和实例数据分析结果显示传统的CV法假阳性问题确实比较严重,原因是CV法在选择调整参数时只考虑了模拟的拟合优度未考虑模型的稀疏性。模拟结果显示pcvl法既能将PSR保持在较高水平又能一定程度地减少FDR,同时其结果受自变量间相关的影响较小,但与EBIC准则、平稳选择法相比其FDR仍然比较高,而且当真实有效应的自变量较多时pcvl法控制FDR的能力略微下降,可能是因为pcvl法通过在CV法的目标函数中加入惩罚项达到拟合优度与稀疏程度的折中,其结果一定程度上依赖于CV法。 EBIC准则γ参数取值不同时结果不相同,当γ=1时其控制FDR的能力与平稳选择法相差不大,但其PSR在小样本时比较低,提示样本量很小时可能会遗漏重要的变量;与γ=1的结果相比,γ取值略大于1-lnn/2lnp时的PSR较高但其FDR也比较高;EBIC准则结果受自变量间相关和稀疏水平影响较大;实例研究结果中EBIC准则只选出1个基因,遗漏掉的重要变量比较多。Luo等[15]将EBIC准则应用于SIS-Adaptive LASSO的调整参数的选择,在其实例分析中γ取值越小筛选的基因数越多,当0.3≤γ≤0.7时只筛选出两个基因,说明该方法确实比较保守。 平稳选择法将FDR控制在低水平的同时仍使PSR保持在可接受水平。该方法降低了模型变量选择结果对调整参数值的依赖性,因此在自变量间不同相关程度和不同稀疏水平的情况下表现均比较稳定,虽然在样本量小且有意义变量多的情况下效能有所降低,但仍高于EBIC准则。 图5 自变量不同稀疏水平下模型变量选择的PSR(100次模拟的平均值) 本研究主要基于LASSO-Cox模型进行四种方法变量选择的比较和评价,然而这些方法不仅可以用于LASSO调整参数的选择,还可以应用于其他惩罚类方法如adaptive LASSO、SCAD(smoothly clipped absolute deviation)、MCP(minimax concave penalty)等,这部分内容将在今后的研究工作中进一步探讨。在利用变量选择方法筛选变量时,除了考虑其统计学意义,还需要结合问题本身的专业知识和实际意义,尤其是面对目前日益庞大的生物学数据,利用变量选择方法筛选出很有可能与癌症患者生存有关联的候选基因后,其具体的生物学意义仍需要进一步实验加以验证。 表1 各方法筛选出的基因 注:粗体字表示平稳选择法、pcvl法、CV法选出的相同基因;斜体字表示pcvl法、CV法选出的相同基因;斜体字加粗表示平稳选择法、CV法选出的相同基因;字体背景灰色表示EBIC准则和pcvl法选出的相同基因;***表示P值小于0.001,**表示P值小于0.01,*表示P值小于0.05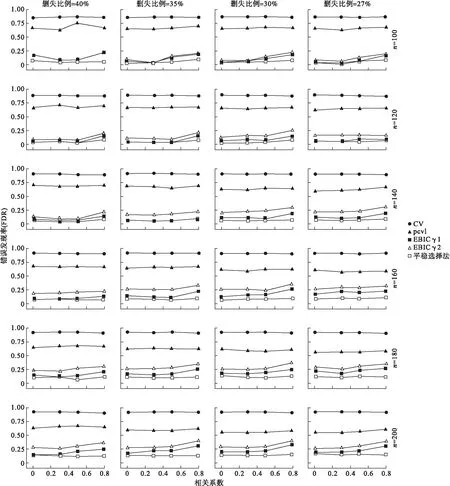
实例分析
1.数据来源及整理


2.实例分析结果

讨 论