一种改进的干涉仪测向基线设计方法
李 超,韦敏峰,李 迪,田德民
(中国船舶重工集团公司第723研究所,扬州 225001)
一种改进的干涉仪测向基线设计方法
李 超,韦敏峰,李 迪,田德民
(中国船舶重工集团公司第723研究所,扬州 225001)
在原有干涉仪测向基线逐级解模糊规则的基础上,在工作频率、无模糊视角范围及相位差误差等条件下,为达到利用较少的天线阵元数解最长基线模糊的目的,提出了一种改进的干涉仪测向基线配置方法,并结合设计实例与已有基线配置方法进行比较,验证了本文的基线配置方法能达到更高的测向精度。
干涉仪;测向;虚拟基线;解模糊
0 引 言
由于精度高、速度快的优点,干涉仪测向在电子战中具有广泛应用。干涉仪测向原理:以不同到达角入射的无线电信号在测向基线上会形成不同的相位差,因此不同的相位差代表不同的到达角[1-2]。在实际测量中,由于鉴相器的测量范围(-π,π ]限制,测量相位差跟实际相位差之间可能差了2π的整数倍,该现象称为相位模糊。短基线可以解决相位模糊问题,但基线长度的缩短会导致测向精度的降低。结合干涉仪解模糊原理[3-5],为解决最大无模糊视角范围与测向精度对天线间距要求这对矛盾,人们提出了一些解模糊方法[6-8]:长短基线法、参差基线法、虚拟基线法及立体基线法等。其中,长短基线法利用长基线保证测向精度,利用短基线解决测向模糊。
对于探测信号频率范围[fmin,fmax]、最大无模糊视角范围θm、θmax、相位差误差±Δφ、测向精度Δθ、阵元间最小间距P的一维多基线干涉仪测向系统,根据fmin、fmax求得λmax、λmin,此时最长基线长度:
(1)
最短无模糊实基线长度:
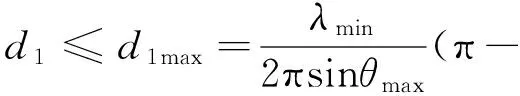
(2)
最短无模糊虚拟基线长度:
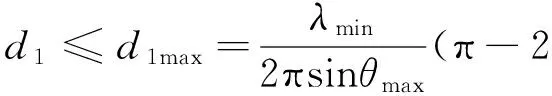
(3)
短基线解长基线模糊的比例系数大小有限制[9],具体情况如下:
实基线解实基线比例系数:
(4)
实基线解虚基线比例系数:
(5)
虚基线解实基线比例系数:
(6)
虚基线解虚基线比例系数:
(7)
在工程应用中,由于指标及器件尺寸等限制,需要改变天线阵元的排列,合理安排基线配置,获得最优的基线配置方法及更高的测向精度。实际应用中,经常由于器件尺寸限制,无法直接构造出最短无模糊实基线,此时需要构造最短无模糊虚基线来完成短基线到长基线的解模糊。为此,本文提出了一种改进的基线配置方法。
1 改进的基线配置方法
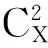
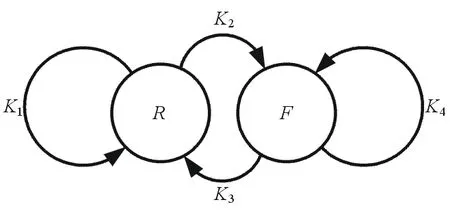
图1 基线逐级解模糊规则示意图
结合实际工程应用条件,构造基于最短无模糊虚基线的基线配置步骤。为方便说明,步骤中的基线长度均用基线长与最短无模糊虚基线长度d1的比值表示。设阵元数为x,令M=dmin/d1max,p=P/d1max,基线配置流程图如图2所示。
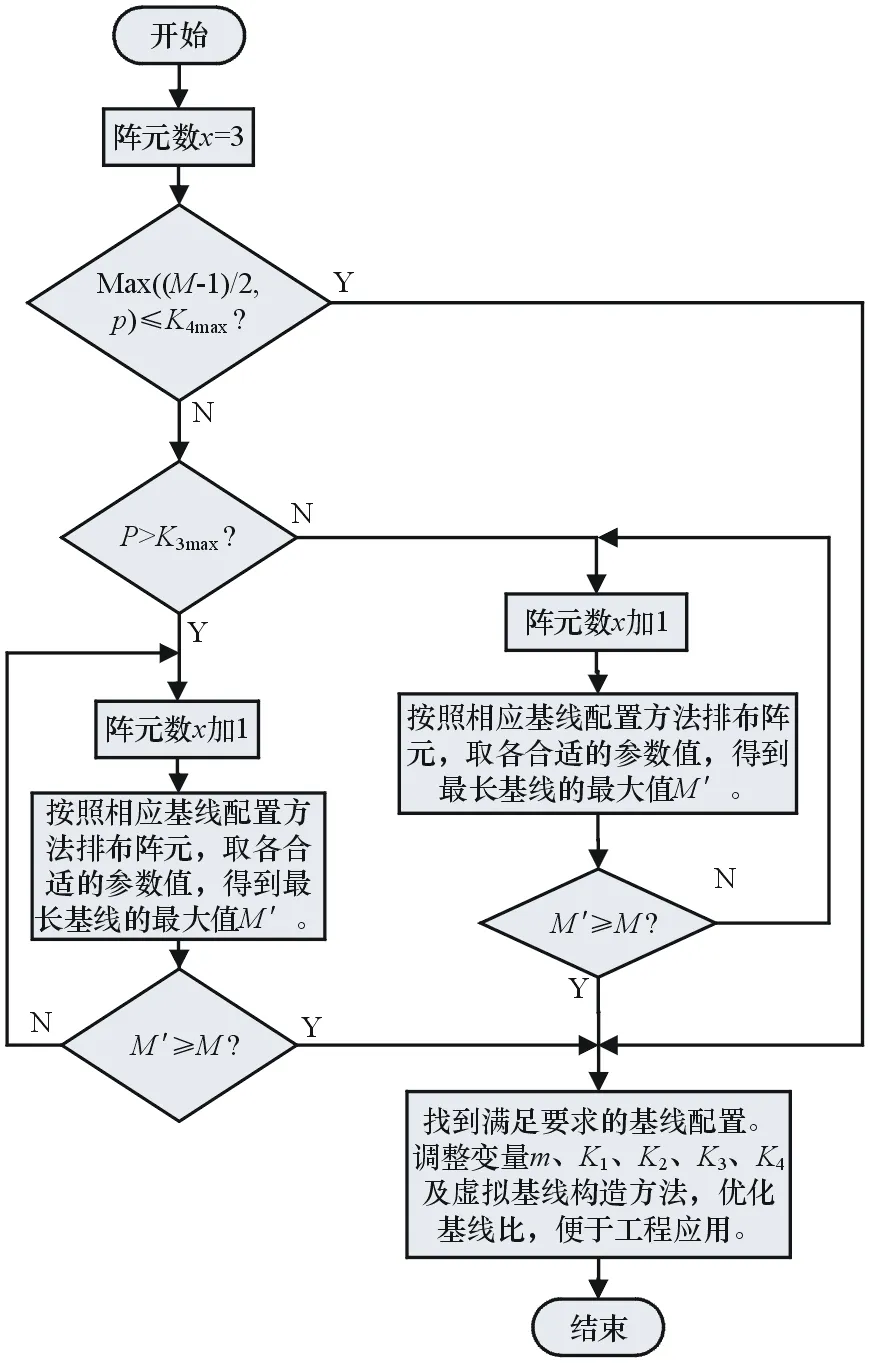
图2 基线配置流程图
(1) 判断3个阵元是否可行
x=3,从3个阵元开始。此时构造出基线m与m+1。
判断方法:
(8)
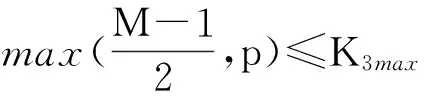
(2) 比较p与K3max的大小
若p>K3max,则转(3);否则转(4)。
(3) p>K3max的基线配置方式
阵元数加1,x ← x+1,在p>K3max时,判断当前数量x个阵元能否构造出满足条件的基线配置。此时,不能直接由最短虚基线解实基线模糊,需要不断构造出更长的虚基线(如1,K4,K42,K43,…),逐级解模糊,最终解实基线m的模糊。令p≤K4aK3,解得:
(9)
取满足a要求的最小整数值为N,令p′=K4NK3。此时利用N+3个阵元即可解得实基线m的模糊。m的变化范围为[ p , p′ ]。可以采用如图3所示基线增长较慢的配置方式。

图3 基线增长较慢的基线配置方式
为了使基线长度尽快增长,可选择不同的虚拟基线构造方式,更快达到最长基线长度M,此时可采用如图4所示的基线配置方式。
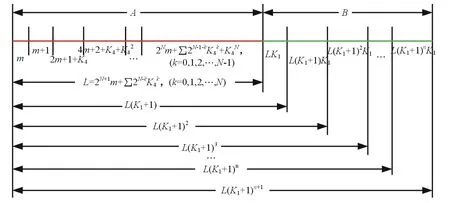
图4 基线增长较快的基线配置方式
图4中,A段基线构造的目的是以最少的阵元数尽快地由虚基线逐级解实基线m模糊;B段基线构造的目的是以最快的速度增长总基线长度,以达到测向精度要求。
考虑当前的阵元数x限制,调整变量,利用图4所述基线配置方法将各段基线长度配置出来。
(a) 当x≥N+3时,即利用不大于x个阵元数便可完成A段由虚基线逐级解实基线m模糊的过程,后续按照图4中B段实基线解实基线模糊的构造方法,即可构造出符合要求的基线配置。

若M′≥M,则基线配置满足要求。
若M′ (b) 当x 此时x个阵元无法构造出满足要求的基线配置,转(3)。 (4) p≤K3max的基线配置方式 阵元数加1,x ← x+1,在p≤K3max时,判断当前数量x个阵元能否构造出满足条件的基线配置。此时,可以直接构造出实基线m,满足由最短虚基线能直接解实基线m的模糊。m的变化范围为[ p , K3max]。 为了使基线长度尽快增长,更快达到最长基线长度M,采用如图5基线配置方式: 图5 基线配置方式 图5中A段基线构造的目的是实现最短虚基线直接解实基线m模糊;B段基线构造的目的是以最快的速度增长总基线长度,以达到测向精度要求。 按照图5所述基线配置方式配置x个阵元,图5中n=x-4,比较此时最长基线(2m+1)(K1+1)x-3的最大值M′与M的大小。 当m=K3max,K1=K1max时,(2m+1)(K1+1)x-3取得其最大值M′=(2K3max+1)(K1max+1)x-3。 若M′≥M,则基线配置满足要求。 此时基线比为K3max,K3max+1,(2K3max+1)K1max,(2K3max+1)(K1max+1)K1max,(2K3max+1)(K1max+1)2K1max,…,(2K3max+1)(K1max+1)x-4K1max,转(5)。 若M′ (5) 调整基线长度 考虑到工程适装性,可在满足基线逐级解模糊规则的前提下,利用变量m,K1,K2,K3,K4以及虚拟基线的构造方式(如图3与图4虚拟基线构造方式有区别)调整基线长度,缩短最长基线长度,使最长基线长度尽量接近M。 为了验证上述基线配置方法的工程有效性,按如下要求设计应用实例。 工作频率为2~6GHz,最大无模糊测向视角范围为±45°,θmax为90°,相位差测量误差为±30°,测向精度为1.5°,阵元间最小间距为61mm,可得信号波长范围为50~150mm。 根据公式(1)~(7): d≥dmin=675.24mm,取d=688mm; d1≤d1max=16.67mm,取d1=16mm; K1≤K1max=5,K2≤K2max=4,K3≤K3max=2.5,K4≤K4max=2。 M=688/16=43;p≥61/16=3.812 5,取p=4。 (1) 判断x=3个阵元能否满足要求 (2) 判断x=4个阵元能否满足要求 因为4>2.5,即p>K3max,此时,由式(9)得:a≥0.68,因此,N=1,p′=2×2.5=5。 此时x=N+3,按照p′,p′+1,2p′+1+ K4max构造基线,各基线比为5∶6∶13。 最长基线长度为M′=5+6+13=24<43,即M′ (3) 判断x=5个阵元能否满足要求 x>N+3,按照p′,p′+1,2p′+1+ K4max,(4p′+2+ K4max)K1max构造基线,各基线比为5∶6∶13∶120。 最长基线长度为M′=5+6+13+120=144>43,满足M′>M,即5个阵元可以满足要求。 (4) 调整基线长度 以基线比为5∶6∶13∶120构造,5+6+13+120=144,144已经远大于最长基线长度要求(M=43)。为考虑工程适装性,将最后一段基线长120缩短至20,可满足测向精度要求,即将基线比调整为5:6∶13∶20,此时亦可满足基线配置要求。 (5) 验证基线逐级解模糊规则 根据5∶6∶13∶20构造基线,可以构造出的实基线为{5,6,11,13,19,20,24,33,39,44},可以构造出的虚基线为{1,2,4,5,6,7,8,9,11,13,14,15,18,19,20,22,24,25,26,27,28,31,33,34,38,39},如图6所示。实基线与虚基线集合中若有相同长度的基线,选实基线误差更小。 图6 实基线与虚基线长 根据基线逐级解模糊规则,由短到长逐级解模糊,基线增长的系数均在K1、K2、K3、K4范围内,最后能够完成最长基线的解模糊。 (6) 对比文献[9]的基线配置方法 根据文献[9],利用5个阵元配置基线。先配置虚拟基线(长度仍用与最短基线长度比值表示):1,2,3,6,9。 第1级实基线为:9×2.5=22.5。 其他实基线为:22.5+1=23.5,22.5+3=25.5,22.5+9=31.5。 最长基线长度为:22.5+23.5+25.5+31.5=103。 因为103<144,因此,在相同数量的阵元数条件下,本文的基线配置方法与文献[9]比,具有更高的测向精度。 本文阐述了干涉仪测向中的基线逐级解模糊规则,为达到利用较少的天线阵元数解最长基线模糊的目的,提出了一种改进的干涉仪测向基线配置方法。结合设计实例,在工作频率范围、无模糊视角范围及测向精度等条件下,验证了本基线配置方法的准确性。与其他基线配置方法比较,本方法具有更高的测向精度。同时,本方法考虑了阵元间间距最小值、相位差误差及工程适装性,具有一定的工程应用价值。 [1] 肖秀丽.干涉仪测向原理[J].中国无线电,2006 (5):43-49. [2] 杨伟程.单站长基线干涉仪测向定位技术研究[D].西安:西安电子科技大学,2009. [3] 张文旭,司锡才,蒋伊琳.相位干涉仪测向系统相位误差研究[J].系统工程与电子技术,2006,28(11):1631- 1632. [4] 李兴华,顾尔顺.干涉仪解模糊技术研究[J].现代防御技术,2008,36(3):92-96. [5] 蒋学金,高遐,沈扬.一种多基线相位干涉仪设计方法[J].电子信息对抗技术,2008,23(4):39-45. [6] 李勇,赵国伟,李滔.一种机载单站相位干涉仪解模糊算法[J].传感技术学报,2006,19(6):2600-2602. [7] 司伟健,初萍.干涉仪测向解模糊方法[J].应用科技,2007,34(9):54-57. [8] 罗贤欣,刘光斌,王忠.干涉仪测向技术研究[J].舰船电子工程,2012,32(8):74-76. [9] 李东虎.干涉仪测向系统中的基线配置技术[J].无线电工程,2014(4):17-19. An Improved Method of Interferometer DF Baseline Design LI Chao,WEI Min-feng,LI Di,TIAN De-min (The 723 Institute of CSIC,Yangzhou 225001,China) Based on the rule of gradually resolving ambiguity of original interferometer direction finding (DF) baseline,this paper puts forward an improved interferometer DF baseline deployment method for the aim of resolving the longest baseline ambiguity by using less antenna array elements under the conditions of operating frequency,range of no ambiguity view,phase difference error,etc.,and compares the method with existing baseline deployment method combining with design example,proves that the baseline deployment method provided in this paper can fetch better DF accuracy. interferometer;direction finding;simulative baseline;resolving ambiguity 2016-08-28 TN971 A CN32-1413(2016)05-0019-05 10.16426/j.cnki.jcdzdk.2016.05.004
2 设计实例
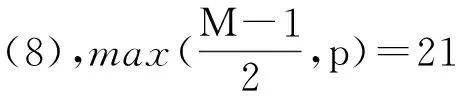

3 结束语

