基于贝叶斯理论的测量误差预报与修正方法

冯 云，朱亦丹，李 将

(中船重工海博威(江苏)科技发展有限公司，扬州 225000)



基于贝叶斯理论的测量误差预报与修正方法

冯 云，朱亦丹，李 将

(中船重工海博威(江苏)科技发展有限公司，扬州 225000)

针对动态测量过程的复杂性以及随机性，提出了基于贝叶斯理论的动态测量误差的建模、预报方法。该方法要求的数据量少，对动态测量误差序列的平稳性没有要求，并且能够充分利用预报过程中的主、客观信息来实时修正模型，提高预报精度。最后，通过Labview仿真验证了基于贝叶斯理论的动态测量误差预报方法具有较高的预报精度。

贝叶斯动态模型；误差预报；动态误差；实时修正

0 引 言

动态测量日益普及，对动态测量精度的要求也越来越高，误差修正是提高动态测量精度的一种有效方法，因此受到普遍关注和高度重视。根据已知的测量误差序列建立动态测量误差模型，并对将来时刻的测量误差进行预报，是实现动态测量误差实时修正的基本方法。国内外专家、学者对动态测量误差的建模预报方法进行了大量研究，并提出了很多有效方法,比如时序分析法[1]、谐波分析法、灰色理论法[2]、神经网络法[3]等现代数学方法。这些方法分别针对特定特征的误差序列提出，具有一定的实用性；但是也存在一些不足，比如需要较多的测量数据，对测量误差序列的平稳性也有要求，模型比较简单，对异常情况的响应差等。另外，由于动态测量误差的随机性和时变性[4]，导致模型的误差预报精度会随着预报步数的增加而快速降低，严重影响了动态测量误差的实时修正效果，成为阻碍进一步提高动态测量误差修正精度的关键所在。对此，本文提出了动态测量误差的贝叶斯建模预报方法。该方法要求的数据量较少,且对误差序列没有平稳性要求，能够充分利用预报过程中的主客观信息来实时修正模型，提高测量误差的预报精度。

1 动态测量误差的贝叶斯建模、预报理论

基于贝叶斯预报理论的动态测量误差预报方法[5],第1步是根据已获取的测量误差序列建立动态测量误差模型。测量误差序列可以通过观测方程和状态方程来描述：

(1)

状态方程:θt=Gtθt-1+ωt

(2)

式中：yt为t时刻动态测量的误差值;本文主要针对单次测量误差序列进行研究，因此，yt和υt是一维变量；θt、ωt的维数以及Ft、Gt根据动态误差序列的特征来决定；υt、ωt分别为观测误差矩阵、状态误差矩阵，它们互相独立。

对于一般的动态测量误差预报方法，要获得θt的初始信息和υt、ωt的先验分布很难，因此本文采用无信息先验分布法进行测量误差的预报。假设误差模型中一共有n个变量，则可以根据n个已知的测量误差值来确定θt、υt以及ωt的初始信息。根据测量误差的特点以及简化推导，假设υt为正态分布N[0,V](V为未知变量)，ωt为均值等于0、方差等于Wt的T分布。由于使用了较少的测量误差数据确定初始信息，并且不可能根据这些数据估计出参数的变化趋势，因此，可以设：Wt=0(t=1,2，…，n)。

设t时刻及之前所有时刻的有效信息集合为Dt，t=0时的初始有效信息集合为D0。根据无信息先验分布法可得：

p(θ1,V|D0)∝V-1(V>0)

(3)

根据贝叶斯理论及测量误差点{y1，y2，…，yn}，可得到p(θn,V|Dn)，进而获得(θn|Dn)和(V-1|Dn)的边缘分布；然后将上述边缘分布作为初始信息，对动态测量误差进行递推预报(t>n)。

设误差数据的初始信息为：

ωt～Tnt-1[0,Wt]

(4)

(θt-1|Dt-1)～Tnt-1[Mt-1,Ct-1]

(5)

(θt|Dt-1)～Tnt-1[At,Rt]

(6)

(V-1|Dt-1)～Γ(nt-1/2,dt-1/2)

(7)

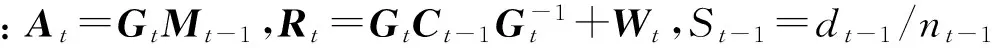
一步向前预报为:

(yt|Dt-1)～Tnt-1[ft,Qt]

(8)

递推修正关系为：

(θt|Dt)～Tnt[Mt,Ct]

(9)

(V-1|Dt)～Γ[nt/2,dt/2]

(10)

Mt=At+Btet

(11)

Ct=(St/St-1)[Rt-BtBtTQt]

(12)

St=dt/nt

(13)

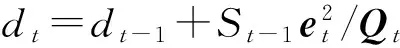
根据公式(9)～(13)可知，递推算法中需要知道Wt(t>n)的值，采用比例因子法，可得：

(14)

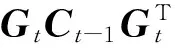
(15)

则：

Wt=GtCt-1GtT(ρ-1-1)

(16)

对于第k(k>0)步向前预报分布：

(θt+k|Dt)～Tnt[At(k),Rt(k)]

(17)

(yt+k|Dt)～Tnt[ft(k),Qt(k)]

(18)

2 软件仿真与分析

2.1 程序设计

本次设计是基于贝叶斯动态误差理论，采用无信息先验分布法，以Labview软件为平台，进行动态测量误差的实时预报与修正。图1所示为动态测量误差贝叶斯预报程序设计流程图。

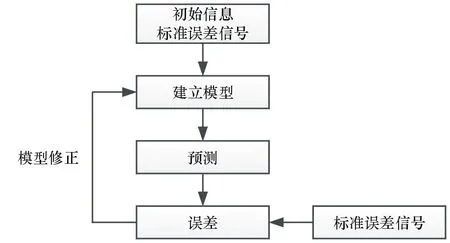
图1 动态测量误差贝叶斯预报程序流程图

2.2 仿真与分析

为了验证动态测量误差建模及预报修正的效果，本文采用周期信号和线性信号的叠加信号对实际效果进行验证。采用的信号为：

y=5sin(20πx)+5sin(40πx)+5sin(80πx)+1·400x

其波形如图2所示。

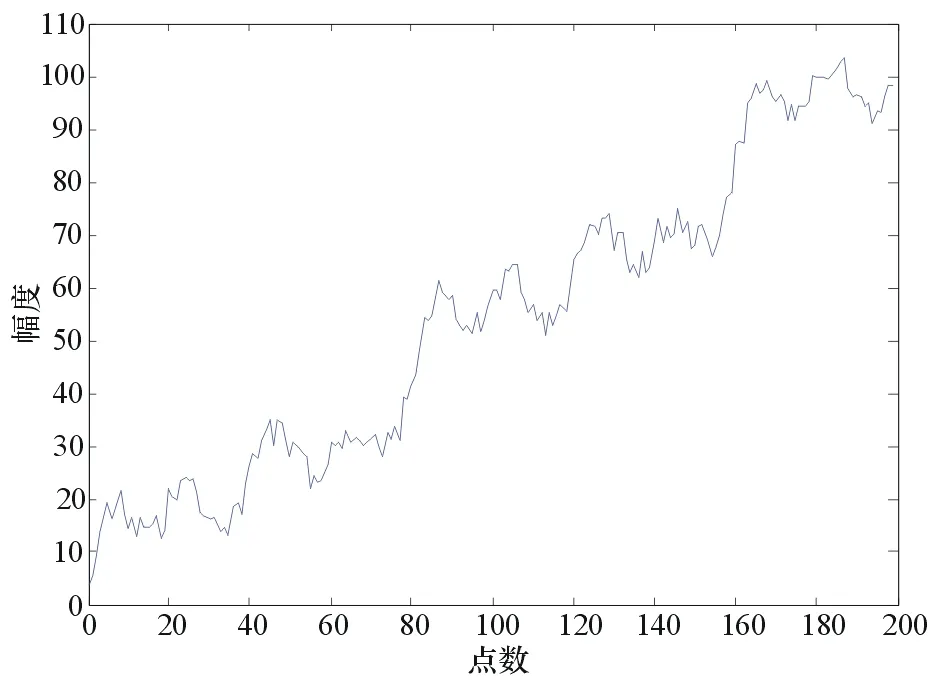
图2 输入信号波形

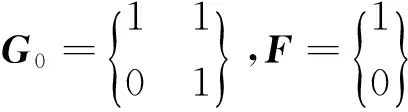
对于周期性模型，周期p=40。根据贝叶斯理论，可求得它有q=p/2=20个调和分量与水平分量。但其主要的调和分量有3个，r=1[y=sin(20πx)]，r=2[y=sin(40πx)]，r=4[ysin(80πx)],则：

(19)

由模型叠加原理可知：G=diag(G1,G2,G3)，F=(1,0,1,0,1,0)T。

对于p=40，其未知参量数目N=2(q-1)+1=39。

对于线性信号和周期信号的叠加信号，根据叠加原理，可以得到：N=3+39-1=41；F=(1,0,1,0,1,0,1,0)T；G=diag(G0,G1,G2,G3)。

运行程序后可得到波形如图3所示。

图3 多步预报波形图

从图3可以看出：从40到80的一步预报效果非常好，和原曲线基本重合，对动态误差序列的模型

建立比较好；从120到200的多步预报中能够反映出原曲线的趋势，预报误差比较小。

3 结束语

本文采用的贝叶斯预报建模方法，对动态测量误差序列没有平稳性要求，使用数据较少，能够快速有效地实时修正误差模型，因此模型的适应性好，能处理异常情况的发生，提高了动态误差实时修正的精度。最后，通过线性信号和周期信号的叠加信号进行了仿真验证，实验结果表明，一步预报和多步预报的结果与实际数据误差不大，预报精度高。由此可知，基于贝叶斯理论的动态测量误差建模预报方法能够非常好地预报动态测量误差。

[1] 卢荣胜.动态测量实时误差修正技术研究[D].合肥:合肥工业大学，1998.

[2] 龚蓬.动态测量误差修正灰色建模理论与应用技术研究[D].合肥:合肥工业大学,1999.

[3] 叶兵.基于遗传神经网络模型实时误差修正任意角测量系统[D].合肥:合肥工业大学,2004.

[4] 费业泰,卢荣胜.动态测量误差修正原理与技术[M].北京:中国计量出版社,2001.

[5] 程真英.动态测量误差修正灰色建模理论与应用技术研究[D].合肥:合肥工业大学,2004.

PredictionandCorrectionMethodofMeasurementErrorsBasedonBayesTheory

FENGYun，ZHUYi-dan，LIJiang

(CSICHebowi(Jiangsu)TechnologyDevelopmentCo.,Ltd,Yangzhou225000,China)

Inviewofthecomplexityandrandomnessofdynamicmeasurementcourse,modelingandpredictionmethodfordynamicmeasurementerrorsbasedonBayestheoryispresented.Themethodrequireslessdata,andthestabilityofdynamicmeasurementerrorssequenceisnotrequired.Themethodcanmakefulluseofthesubjectiveandobjectiveinformationtocorrectthemodelinrealtime,improvesthepredictionaccuracy.Finally,LabviewsimulationresultprovesthatthepredictionmethodofdynamicmeasurementerrorsbasedonBayestheoryhasbetterpredictionaccuracy.

Bayesdynamicmodel；errorprediction；dynamicerror；realtimecorrection

2016-05-27

TP

A

CN32-1413(2016)05-0064-03

10.16426/j.cnki.jcdzdk.2016.05.016