基于线阵的多波束比幅法圆锥误差分析
王 开,邵文建,朱 峰
(1.中国船舶重工集团公司第723研究所,扬州 225001;2.解放军92602部队,宁波 315000)
基于线阵的多波束比幅法圆锥误差分析
王 开1,邵文建1,朱 峰2
(1.中国船舶重工集团公司第723研究所,扬州 225001;2.解放军92602部队,宁波 315000)
在一维线阵条件下,利用多波束比幅法测量方位角时,随着入射信号仰角变大,方位角测量误差会变大。分析了不同仰角下的波束偏离,提出了利用“修正角度”减小圆锥误差的方法,并比较修正前后测量误差统计值,说明达到了提高方位角测量精度的效果。
多波束比幅;圆锥效应;天线
0 引 言
在现代战争中,电子对抗的作用变得越来越重要,而电子侦察是电子对抗的重要环节[1]。其中测向精度是电子侦察的关键指标之一,直接关系到所测威胁目标方位和引导干扰机干扰方向的精度。基于线阵的多波束比幅测向法因其结构和处理都比较简单,在电子侦察设备中广泛应用,但其本身也存在固有缺陷,本文将对这方面进行分析。
1 多波束比幅测向原理
假设阵列天线包含N个天线单元,则同时存在的N个波束覆盖了需要侦察的空域Ω(°),每个波束的轴线角度分别为θ0、2θ0、…,Nθ0,其中θ0=Ω(°)/N。三波束比幅测向法原理是通过比较相邻的3个天线单元接收到的信号幅度来确定入射信号的到达角度。假设辐射源信号的到达角θ位于第n个波束的轴线附近,如图1所示。
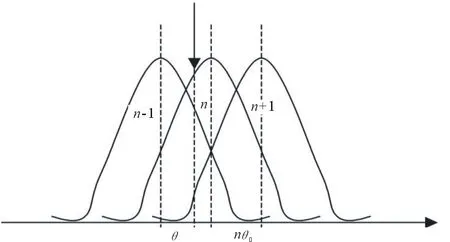
图1 三波束比幅测向原理图
多波束测向系统要求每个天线及其接收通道具有严格一致的幅度特性,因此在分析三波束比幅测向原理时先假设各通道幅度特性一致[2]。
通常认为在一定范围内,多波束天线的方向图是高斯型的,且相对于天线轴线对称,因此第n个天线及其相邻的第n-1,n+1个天线接收到的信号幅度可表示为:
An(θ)=Ane-k(θ-nθ0)2
(1)
An-1(θ)=An-1e-k[θ-(n-1)θ0]2
(2)
An+1(θ)=An+1e-k[θ-(n+1)θ0]2
(3)
式中:An-1,An,An+1为各天线及接收通道的增益;k为比例常数。
将式(1)和式(2)两边取对数后相减得:
ΔL=lgAn-lgAn+1-k[θ-nθ0]2+ k[θ-(n-1)θ0]2
(4)
由于假设各通道幅度特性一致,则式(4)可以化简为:
(5)
(6)
将式(1)和式(3)两边取对数后相减得:
ΔR=k[(2n+1)θ02-2θθ0]
(7)
(8)
将式(6)和式(8)相加得:
(9)
将式(6)代入式(8)得:
(10)
将式(10)代入式(9)得:
(11)
从式(11)可以看出,通过相邻3个天线接收信号的比幅计算,结合判断最大信号的波束号就可以确定辐射源信号的到达角。
2 线阵的缺陷

图2 线阵组成示意图
天线系统是一个由24个垂直放置的扇形喇叭在水平面上排列组成的线阵,如图2所示。每个阵元通过同相电缆连接到固定的波束形成透镜系统。
线阵天线的一个最重要的基本特性是天线方向图关于垂直于线阵的轴对称,而且越靠近线阵边缘波束间的间隔越大,线阵方向图如图3所示。所以线阵有一个缺陷:当辐射源从线阵的轴线向边缘移动时,测向误差会变大。
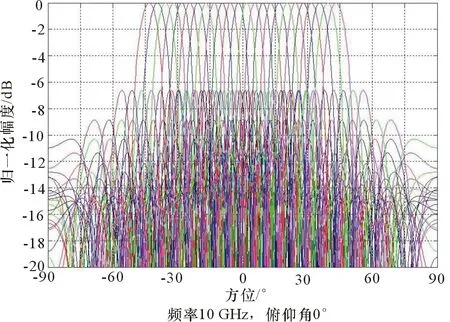
图3 线阵方向图
在一维线阵条件下,只能测量辐射源信号的方位,而随着入射信号仰角变大,其方位角会慢慢远离天线轴线,导致方位角测量误差变大,这种方位角随仰角变化的现象通常被称为圆锥效应。表1为入射信号为10 GHz时,测量的方位误差与入射信号仰角之间的关系。

表1 不同仰角情况下方位角测量误差
上述线阵的2个固有误差在辐射源入射角为(42.7°,30°)的情况下可达到8.7°,实际应用中显然是不能接受的。
3 圆锥误差分析与修正
通过天线测试系统测量出在不同方位、仰角角度时线阵每个喇叭天线的幅度值,并采用三波束比幅法计算出方位值。由于三波束比幅法需要相邻3个天线接收信号的幅度值,所以1号和24号波束的方位值无法算出。结果如表2所示。
从表2可以看出,在仰角为0°和5°的情况下,波束不发生偏离;在仰角大于等于10°的情况下,波束就会发生偏离。例如,3号波束在仰角为0°时上报的波束号为3,但在仰角为30°时上报的波束号为4或者5,这就是所谓的“圆锥效应”,而且越靠近线阵边缘的波束(2、23号)圆锥效应现象越明显。
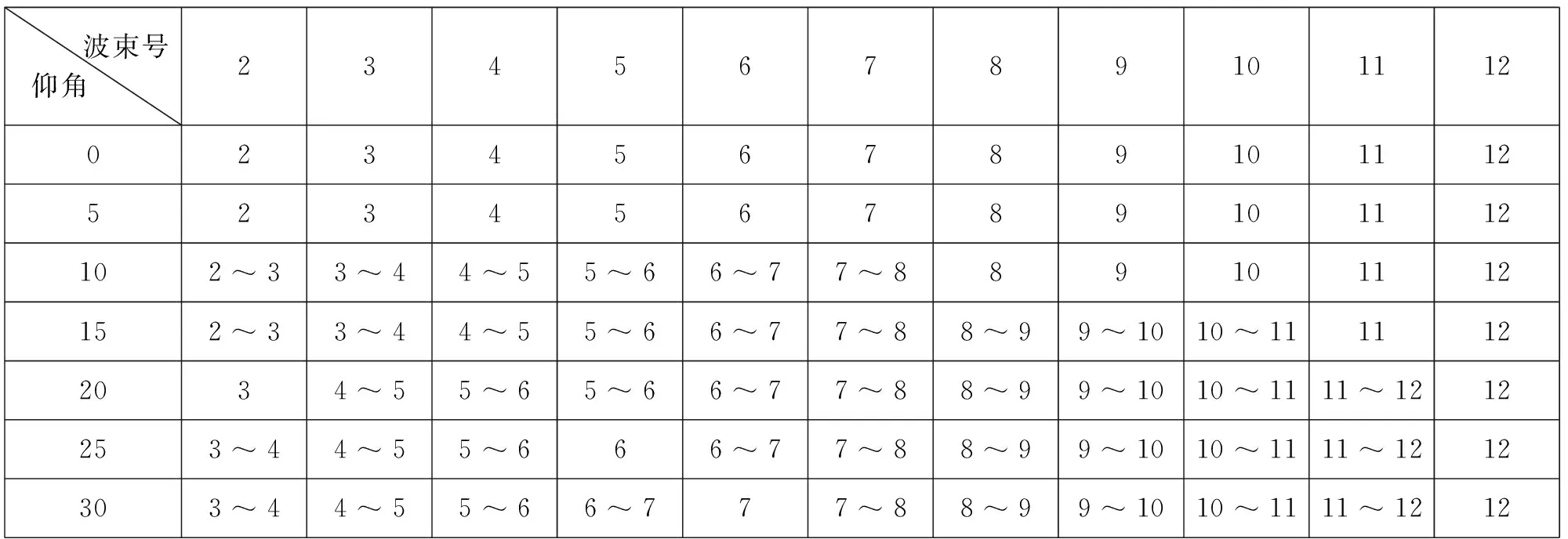
表2 不同仰角情况下的波束偏离

波束号仰角 131415161718192021222301314151617181920212223513141516171819202122231013141516171818~1919~2020~2121~2222~231513141515~1616~1717~1818~1919~2020~2121~2222~2320131414~1515~1616~1717~1818~1919~2020~2121~2222~23251313~1414~1515~1616~1717~1818~1919~2019~2020~2121~22301313~1414~1515~1616~1717~18181919~2020~2121~22
本文提供一种减小圆锥误差的方法。假设在线阵波束覆盖范围内,当有仰角大于等于10°的信号存在时,一个“修正角度”将会被代入三波束比幅法中计算。例如,入射信号的真方位在(30°,30°),利用“修正角度”计算,然后上报波束号为21。这个波束号与仰角为0°时的波束号一样。这样会从根本上减小圆锥误差,提高仰角威胁目标的方位测量精度。表3为利用“修正角度”计算得到的不同仰角情况下的方位角测量误差。

表3 修正后不同仰角情况下方位角测量误差
对比表3和表1可以看出,利用“修正角度”后高仰角入射信号的方位测量误差有所减小,而且仰角越大效果越明显。
上文中提到过线阵的1号和24号波束的方位值无法利用三波束比幅法算出,但当线阵按照4个象限安装时这个问题可以得到解决。如图4所示,第一象限线阵的23、24号天线和第二象限线阵的1、2号天线同时收到入射信号。

图4 相邻象限线阵示意图
首先通过比较第24号和1号天线接收信号的幅度值确定信号在第一象限还是第二象限,若信号在第一象限则利用第一象限23、24和第二象限1号天线计算出入射信号方位角;反之,则利用第二象限1、2和第一象限24号天线计算出入射信号方位角。在进行上述计算式时要加入“修正角度”。
4 结束语
本文介绍了一种减小线阵条件下多波束比幅法测向圆锥误差的方法,这种方法简单易行,可以在工程应用中实现。电子侦察要获得更高的测向精度还需对影响的其他因素进行分析和工程实践中的不断调试。
[1] 赵国庆.电子对抗原理[M].西安:西安电子科技大学出版社,2003.
[2] 顾敏剑.多波束比幅测向系统精度分析[J].舰船电子对抗.2007,30(3):70-73.
Cone-error Analysis of Multi-beam Amplitude-comparison Method Based on Linear Array
WANG Kai1,SHAO Wen-jian1,ZHU Feng2
(1.The 723 Institute of CSIC,Yangzhou 225001,China;2.Unit 92602 of PLA,Ningbo 315000,China)
Under the condition of one-dimensional linear array,when the azimuth is measured by using multi-beam amplitude-comparison method,the measurement error of azimuth will increase along with the elevation of incident signal.This paper analyzes the beam deviation under different elevations, puts forward a method to reduce the cone error by using the "correction angle",and compares the statistical value of measurement error after and before correction,shows that the method fetches the effect raising the azimuth measurement accuracy.
multi-beam amplitude-comparison;cone effect;antenna
2016-06-23
TN82
A
CN32-1413(2016)05-0031-03
10.16426/j.cnki.jcdzdk.2016.05.007

