基于MUSIC算法的圆阵DOA估计技术及改进方法

糜坤年，张 磊

(中国船舶重工集团公司第723研究所，扬州 225001)



基于MUSIC算法的圆阵DOA估计技术及改进方法

糜坤年，张 磊

(中国船舶重工集团公司第723研究所，扬州 225001)

介绍了基于MUSIC算法的圆阵到达方向(DOA)估计技术，即将均匀圆阵接收数据的协方差矩阵进行特征分解，把观测数据划分为信号子空间与噪声子空间，并利用2个空间的正交性构造出"针状"空间谱峰，进行信号源DOA估计；针对小信噪比和小快拍数情况下，常规MUSIC算法对入射角度相近的信号源的分辨率严重下降的问题，利用谱函数极大值点对方位角和仰角的二阶导数小于零的特性，通过对方位角和俯仰角求二阶偏导数，提出了新的空间谱函数的方法。

MUSIC算法；DOA估计；均匀圆阵

0 引 言

电磁波是雷达系统中承载信息的媒介，空间到达角是其重要的特征参量，携带了信号重要的信息。空间到达角描述了信号源的空间位置，用参量(θ，φ)表示，分别表示俯仰角和方位角。阵列信号处理估计是近几十年发展起来的一门新兴信号处理理论。到达方向(DOA)估计是阵列信号处理的一个重要领域，它在雷达、通信、声纳及地震方面的应用越来越受到重视。其主要目标是研究提高在处理带宽内的空间信号的估计精度、角度分辨率和提高运算速度的各种算法。常规的空域谱分析是一类线性谱估计，这种谱估计受瑞利限约束。为了突破这个限制，国内外学者进行了大量的研究，并获得了丰富的研究成果，其中最具革命性意义的是1979年美国Schmidt R O等人提出的多重信号分类(MUSIC)算法[1]，实现了真正意义的阵列高分辨测向。MUSIC算法从几何角度分析了估计问题的内在结构，即通过阵列协方差矩阵的特征分解把观测数据空间划分为信号子空间和噪声子空间，然后利用这2个空间的正交性构造出“针状”空间谱峰，从而实现了DOA的超高分辨率估计。同时利用圆阵测量估计信号源的到达角信息与均匀线阵相比具有很大的优越性：第一，均匀圆阵是一个平面阵，它可以同时提供方位角和俯仰角信息；第二，均匀圆阵提供的方位角信息是360°全方位、无模糊的[2]。然而，由于受阵列孔径的限制，MUSIC算法在信噪比较低或者是快拍数较小时，对角度相近的2个信号源的分辨率不高。为此，有学者针对该问题，提出了基于MUSIC算法的改进算法，即利用MUSIC谱函数极大值点对方位角和仰角的二阶偏导数小于零的特性，通过对方位角和俯仰角求二阶偏导数，构造新的空间谱函数的新方法[3]。

1 信号接收模型

M个各向同性的阵元均匀分布在一个半径为r的圆周上，如图1所示。采用球坐标系来表示平面波的到达方向，圆形阵列的圆心位置位于坐标系的原点，信源的俯仰角φ∈[0,π/2]是Z轴与信号源入射方向的夹角，而方位角θ∈[0,2π]是从X轴沿逆时针方向到信源入射方向在阵列平面上投影的夹角[4]。第M阵元与圆心之间的连线与X轴的夹角为：

(1)

其位置矢量为pm=(rcosγm,rsinγm,0)。

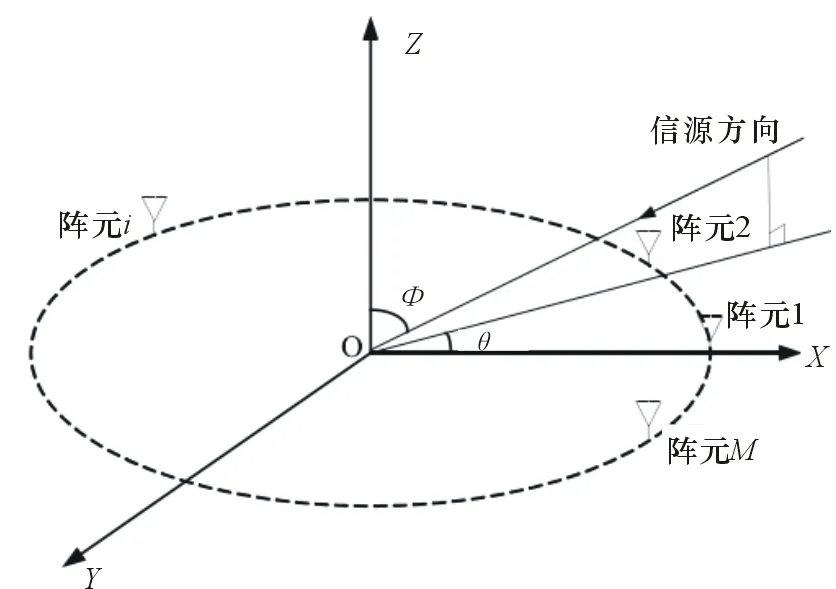
图1 均匀圆阵结构模型

假设一远场窄带信号从γ=(sinφcosθ,sinφsinθ,cosφ)为一单位矢量，则信号在第m个阵元接收信号与圆心处接收信号的复包络之间的相位差为:

ψm=e-j2πf0τm=e，

m=0,1,2,…,M-1

(2)

式中：f0为载波中心频率；λ为载波波长。

则圆阵的方向矢量为:

α(θ,φ)=[ee…e]T

(3)

假设有D个入射远场窄带信号且互不相干，则可以得到第k个阵元在t时刻接收信号为:

(4)

矩阵形式：

X(t)=AS(t)+N(t)

(5)

式中：X(t)=[x1(t),x2(t),…,xM(t)]T；A=[a(θ1,φ1),a(θ2,φ2),…,a(θD,φD)]；S(t)=[s1(t),s2(t),…,sM(t)]T。

2 经典MUSIC算法

由以上讨论可知，阵列接收数据的矩阵形式为：

X(t)=AS(t)+N(t)

(6)

则阵列数据的协方差矩阵为：

R=E[XXH]=AE[SSH]AH+δ2I=ARSAH+δ2I

(7)

由于信号不相干且与噪声相互独立，数据协方差矩阵可分解为信号、噪声两部分。

对R进行特征分解得：

R=ARSAH+δ2I=USΣSUSH+UnΣnUnH

(8)

又由于噪声子空间与信号子空间正交，故有：UnA(θ,φ)=0，(θ,φ)∈{(θ1,φ1),(θ2,φ2),…,(θD,φD)}。但实际接收数据矩阵是有限长的，即数据协方差矩阵的最大似然估计为：

(9)

式中：L为快拍数。

对R进行特征分解后得到的噪声子空间特征矢量矩阵Un。由于噪声的存在，UnA(θ,φ)并不完全正交，由此可以定义出MUSIC空域谱表达式：

(10)

3 改进型MUSIC算法

经典MUSIC算法在信噪比较高、快拍数较多的情况下可得到良好的信号分辨率、测量精度，但在信噪比较小、快拍数较少的情况下，信号分辨率和测量精度会严重降低。以二维MUSIC空域谱为例，2个独立入射信号源入射到八阵元的均匀圆阵上，阵圆半径与载波波长关系r=2λ,θDOA分别为θ1=66°，φ1=60°；θ2=60°，φ2=60°。

如图2所示可知，当信噪比和快拍数较大时，经典MUSIC算法的空域谱有2个尖锐的谱峰，可将2个入射角相近的信号源分离；当信噪比和快拍数较小时，基于经典MUSIC算法的空域谱的谱峰不够尖锐(如图2)，难以区分，无法将2个入射角相近的信号源分离开来；但通过对图2中谱峰的观察，可以看出：在整个谱曲面上，空域谱在取得极大值处光滑；因此可以根据光滑极大值点二阶导数小于0的特性，在谱峰处分别对俯仰角和方位角求二阶导数，构造新的空域谱，以增加相近信号的分辨率。

图2 经典MUSIC算法仿真图

假设俯仰角φ的范围为Rφ,搜索间隔为Δφ；方位角θ的范围为Rθ，搜索间隔为Δθ。

由二元离散函数对变量求偏导数可得，在(φk,θn)处离散函数P对自变量φ的一阶偏导数为:

(12)

(13)

(14)

(15)

(16)

(17)

由于P对φ和θ求二阶偏导是相互独立的，所以可以将原谱函数的二阶导数P″表示为:

(18)

由以上公式可构成新的空域谱函数；改进方法的基本思想是对MUSIC谱函数极大值点处对方位角和俯仰角求二阶偏导，并利用二阶偏导小于0的特性，构成新的空域谱函数，再对新谱函数进行峰值搜索，得到信号源DOA[5-6]。

4 仿真与分析

仿真阵列采用阵元数为8的均匀圆阵，阵圆半径r=2λ，λ为窄带信号载波波长，噪声为高斯白噪声，求导点的领域l=1。

4.1 精度分析

假设有一个远场窄带信号源，DOA为θ1=65°，φ1=30°；L=500的条件下，经典MUSIC算法和改进算法的均方根误差随SNR变化比较图见图3。

观察图3(a)、(b)可知：在L=500时，经典MUSIC算法和改进型MUSIC算法测量的俯仰误差、方位误差均随信噪比的增加而减小；并且在给定信噪比的情况下，2种算法的均方误差大小相近，则2种算法有着相近的测量精度。

图3 经典MUSIC算法和改进MUSIC算法均方根误差比较图

4.2 分辨率分析

假设有2个远场窄带信号源，DOA分别为θ1=66°，φ1=60°，θ2=60°，φ2=60°，对2个信号分别使用经典MUSIC算法和改进MUSIC算法进行空间谱估计。经典MUSIC算法和改进MUSIC算法仿真结果对比图如图4所示。

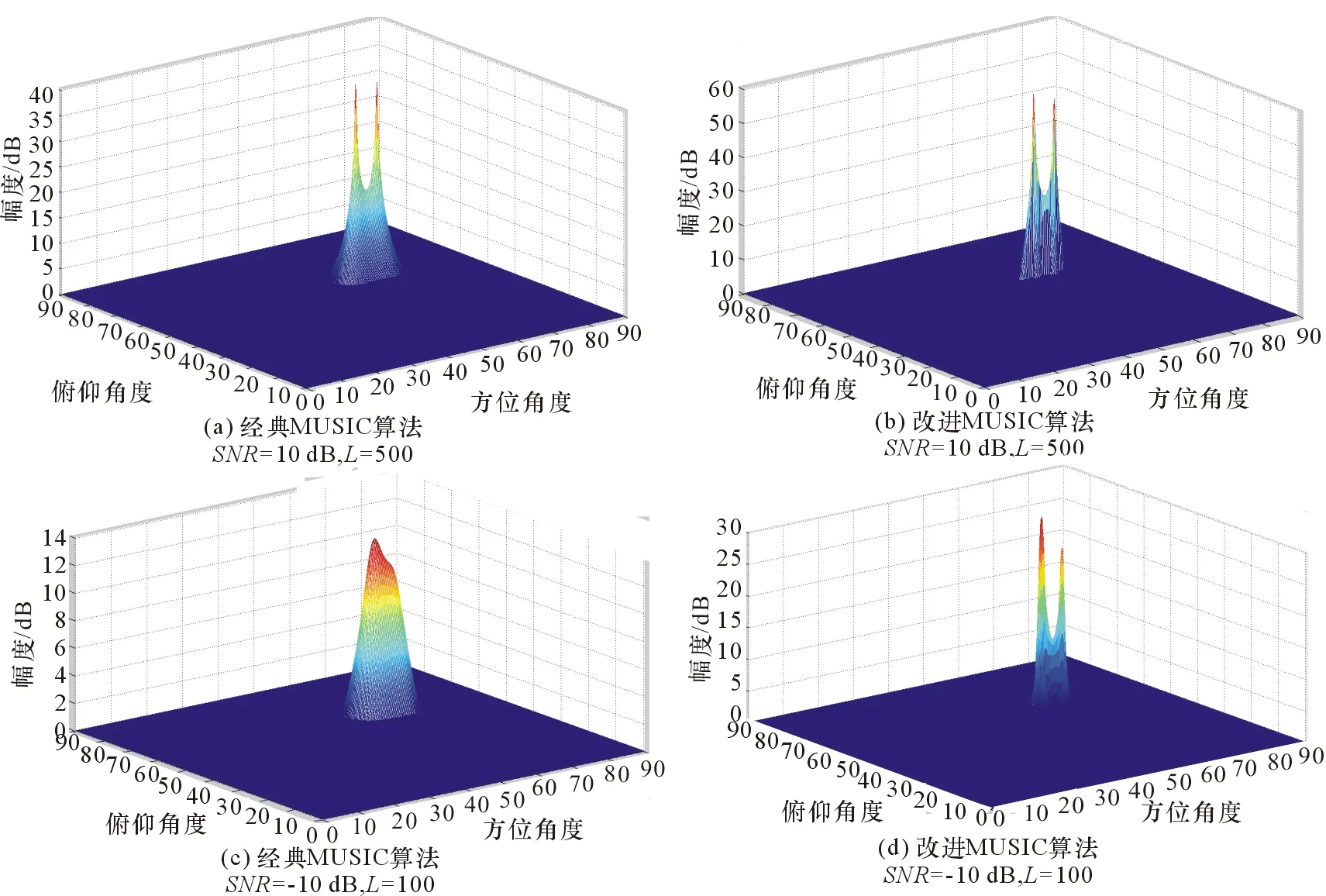
图4 经典MUSIC算法和改进MUSIC算法仿真结果对比图

观察图4(a)、(b)可知，在信噪比、快拍数较高的理想情况下，2种算法的空间谱都出现了2个独立的谱峰，则均对相近信号具有良好的分辨率；但在信噪比、快拍数较低的非理想情况下，对角度相近的两信号源进行DOA估计时(图4(c)、(d))，经典MUSIC算法的空间谱只有一个谱峰，无法有效将2个信号源分开；但在改进MUSIC算法空间谱中，出现了2个独立谱峰，可将2个信号源准确地分开。

5 结束语

经典MUSIC算法在信噪比较高、快拍数较大时，对信号入射角的二维空间谱估计具有良好的分辨率和测量精度，但在信噪比、快拍数较小时，其二维空间谱的分辨率会严重下降。本文针对该问题，提出了利用谱函数极大值点对方位角和仰角的二阶导数小于零的特性，通过对方位角和俯仰角求二阶偏导数，构造新空间谱函数的新方法。仿真实验说明，改进MUSIC算法在不改变经典MUSIC算法精度的前提下，可给出更好的分辨率。

[1] 刘德树，罗青云，张剑云.空间谱估计及应用[M].合肥：中国科学技术大学出版社，1997.

[2] 徐青.基于均匀圆阵的DOA估计算法研究[D].成都：电子科技大学学报，2008.

[3] 司伟建，蓝晓宇，刘学.提高二维DOA估计分辨率的改进MUSIC算法[J].西安电子科技大学学报，2012，39(2)：138-144.

[4] 宋海岩，时洁，刘伯胜,等.稳健空间谱估计技术及其应用[M].哈尔滨：哈尔滨工程大学出版社，2014.

[5] 张小飞，陈华伟，仇小锋,等.阵列信号处理及MATLAB实现[M].北京：电子工业出版社,2015.

[6] 徐振海.极化域-空域联合谱分辨力研究[D].长沙：国防科技大学，2004.

Estimation Technology and Improved Method of Circle Array DOA Based on MUSIC Algorithm

MI Kun-nian，ZHANG Lei

(The 723 Instiute of CSIC，Yangzhou 225001，China)

This paper introduces the estimation technology of circle array direction of arrival (DOA) based on MUSIC algorithm,namely performs the characteristic decomposition to covariance matrix of the data received from uniform circle array,divides the data into signal subspace and noise subspace,and uses the orthogonality of two spaces to form the acicular space peak,performs the estimation of signal source DOA.Aiming at the problem that resolution of signal sources with adjacent incident angles decrease greatly by using conventional MUSIC algorithm in the conditions of small signal to noise ratio and snapshot number,this paper uses the characteristic that second-order partial derivative of spectrum function maximum point to azimuth angle and elevation angle is less than zero,presents a new spatial spectrum function method by taking the second-order partial derivative of azimuth angle and elevation angle.

MUSIC algorithm；direction of arrival estimation；uniform circle array

2016-03-23

TN971.1

A

CN32-1413(2016)05-0024-04

10.16426/j.cnki.jcdzdk.2016.05.005