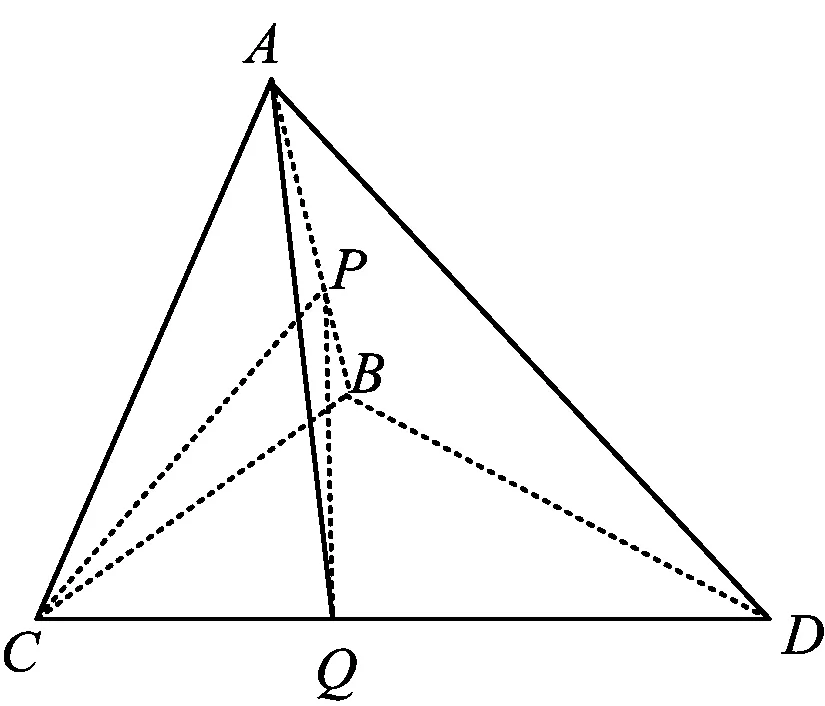
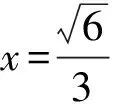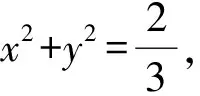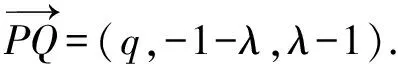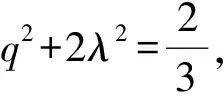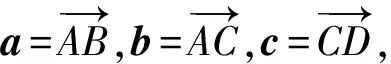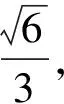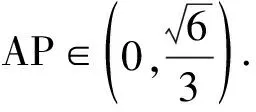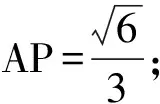一道动态立体几何问题解决的7个视角与思考*
●
(仙居中学,浙江 仙居 317300)
题目如图1,在三棱锥A-BCD中,平面ABC⊥平面BCD,△BAC与△BCD均为等腰直角三角形,且∠BAC=∠BCD=90°,BC=2,点P是线段AB上的动点,若线段CD上存在点Q,使得异面直线PQ与AC成30°角,则线段PA长度的取值范围是______.
(2017年2月浙江省温州市数学高考模拟试题第8题)

图1 图2
视角1从定义出发,探寻自然的解题方法.
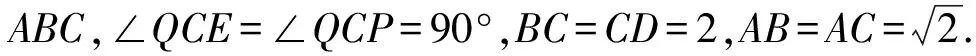
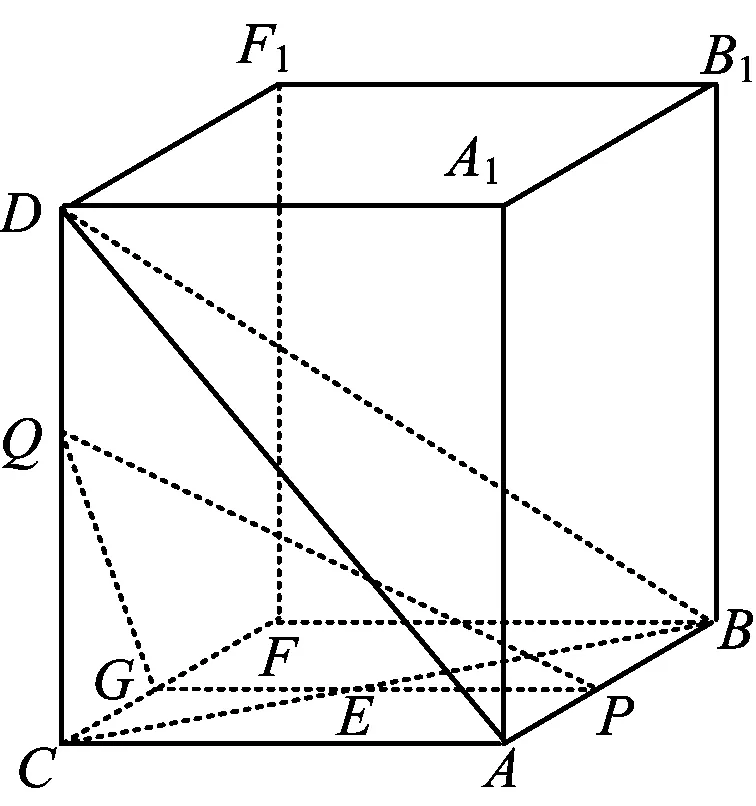
设AP=x,CQ=y(其中0 从而 由余弦定理得 EQ2=PQ2+PE2-2PE·PQcos 30°, 化简得 于是 视角2从坐标出发,探寻动点的本质联系. 图3 因为异面直线PQ与AC成30°角,所以 化简得 由0≤q≤2,知 视角3从向量出发,突破空间的条件限制. 化简得 即 故 联结CP,则在Rt△PCQ中, 又在Rt△PAC中, 得 即 视角4从极限出发,探寻动点的变化趋势. 图4 视角5从射影出发,借助三余弦定理探求角之间的联系. 图5 解法6由题意可知CD⊥面ABC,故转换视角重新作图(如图5).联结CP,则∠CPQ即为直线PQ与底面ABC所成的线面角,记作θ.设异面直线PQ与AC所成的角为θ1,直线PQ在底面的射影PC与直线AC所成的角为θ2,即θ2=∠ACP,则由三余弦定理可得 cosθ1=cosθ·cosθ2, 从而θ1≥θ2.又θ1=30°,则 θ2≤30°, 从而 于是 图6 评注本题换个角度转化成三棱锥D-ABC,容易看出直线PQ在底面的射影为直线CP,由三余弦定理得直线PQ与AC所成的角θ1大于等于其射影CP与直线AC所成的角θ2,从而把条件中的等量关系θ1=30°转化为不等关系θ2≤30°,由此得出AP的范围.空间中点、线、面的位置关系,通过它在平面上的射影揭示出它们之间的内在规律,这是一种重要的研究事物的思想方法.在动态立体几何问题中,选择恰当的投影面,很多时候可以把空间中运动的量转化为投影面上静止的量,把空间中混沌的关系转化为其射影明确的关系. 视角6从轨迹出发,探寻解析几何与立体几何的交汇. 图7 评注双动点问题中固定其中的一个动点,让另一个点先动起来是常见的一种想法.本题中,固定点P后,把点Q的运动转化为直线PQ绕着轴PE旋转,得到一个圆锥曲面,由平面BCD去截这个圆锥,从而得到点Q的一个运动轨迹为椭圆,再由直线CD与椭圆相交确定点Q.在动态立体几何中,很多问题往往需要结合解析几何中曲线的定义,通过构造圆锥模型来确定动点的位置及运动轨迹,这样容易发现隐含的几何性质,更有利于找到最值点和临界点,从而使解题过程得到优化[2]. 视角7从整体出发,探寻问题的几何本质. 解法8在图5基础上,将直三棱柱补形成长方体ABFC-A1B1F1D(如图7),过点P作PG∥AC交BC于点E,交CF于点G,则PG⊥面CFF1D,且∠QPG即为异面直线PQ与AC所成的角.在Rt△PGQ中, 得 在Rt△QCG中, 即 评注在立体几何中,一种常见的补形是将锥体补形成柱体,将三棱柱补形成长方体或正方体,将局部的图形补形成一个整体,从整体出发探究动点运动变化中的不变量.本题中,从三棱锥这一局部角度看,PE和QE是两条变化的线段,∠QPG=30°这一条件得不到一个明确的结论,而从长方体这一整体角度分析,由∠QPG=30°知线段PG,QG的长度是定值,因此本题的几何本质是PQ在面CFF1D上的投影长为定值,问题马上得到解决.从整体角度看问题,胸有全局,眼界更宽广一点,思维更开阔一点,解法就更简单一点. “动态”充满着神奇,孕育着创造.动态立体几何问题情景新颖、解法灵活、极富有思考性和挑战性,能更好地考查学生的空间想象能力和思维能力[3].对动态立体几何问题要多作解题研究,要善于从各个不同的视角出发加以分析,既要从数的角度来关注运动变化过程中变量的本质变化与变量间的联系,也要从形的角度来关注运动变化过程中动点的运动轨迹与不变的几何关系,还要从极限或整体的视角出发思考,从而使问题得到灵活的解决. 参 考 文 献 [1] 袁方程,黄俊峰.解决立体几何中“动态问题”的常用策略[J].河北理科教学研究,2012(6):6-9. [2] 吉俊杰.“空间运动”与“圆锥”的“不解之缘”——由2016年浙江高考谈“动态”立体几何教学建议[J].中学数学,2016(11):81-83. [3] 马茂年,吴晓明.动态几何 策略引领 理性探索——例说立体几何“动态”题型解题策略[J].中学教研(数学),2014(2):1-4.