2017年浙江省数学高考压轴试题命题手法再探究*
●
(泉州实验中学圣湖校区,福建 泉州 362000)
笔者从命题角度对2017年浙江省数学高考压轴试题进行了分析,追根溯源,发现本题源自数列不动点的解题思想,将数列、函数、不等式等知识进行交汇,并从中提炼、设置问题[1].下面笔者展示对该题命题方法的思考过程,并根据此命题方法命制了两道相关新题,这对于高三复习是有启发意义的.
1 试题展示
题目已知数列{xn}满足x1=1,xn=xn+1+ln(1+xn+1)(其中n∈N*),证明:当n∈N*时,
1) 0 (2017年浙江省数学高考试题第22题) 本题的题源当从一类递推数列说起. 即 从而 又x1=1,故 从而 为增强题目的综合性,体现试题的区分度,有效考查学生分析问题、解决问题的能力,命题者引入了函数、不等式等知识进行交汇.因此,需要选择恰当的函数模型,使得xn=f(xn+1),且满足递推数列的不等式关系,即 从而可确定函数 f(x)=ln(x+1)+x, 即 xn=xn+1+ln(1+xn+1),x1=1. 不等式通过适当变形即为文首高考试题第2)小题的设置. 图1 图2 2x>ln(x+1)+x, 即 xn=xn+1+ln(1+xn+1)<2xn+1, 从而 亦即 相乘得 为了能够更全面地考查证明不等式的方法,并使部分中等生得到相应分,有效体现区分度,因此设置了第1)小题. 经过上述步骤,便完成了2017年浙江省数学高考压轴题的命制. 经历了上述试题的探究过程,我们掌握了试题的一种命题方法[2].应用同样的方法,笔者命制了两道试题,供读者赏析. 1) 1 2) 2an+1an<3an-an+1; g(x)≥g(1)=1. 若存在n0∈N*,且n0≥2,使得an0=1,则 由g(x)的单调性可知an0-1=1,即 an0=an0-1=…=a1=1, 与已知a1=2矛盾,故对任意n∈N*,an≠1,从而an>1.又 从而f(x)在(0,+∞)上单调递减,由f(1)=0及an>1,得f(an)<0,即an+1-an<0. 综上可得1 再令F(x)=4x3-3x2-3x-1,其中1 F′(x)=3(4x2-2x-1). 因为F′(x)在(1,2]上单调递增,所以 F′(x)≥F′(1)=3, 从而F(x)在(1,2]上单调递增.又 F(1)=-3<0,F(2)=13>0, 由1 h(an)<0, 即 即 2an+1an<3an-an+1. 3)由第2)小题得 变形得 即 1) 0 2) 2an-4an+1≤anan+1≤2(an-an+1); 证明1)(数学归纳法)当n=1时,a1=1>0. 假设当n=k时,原不等式成立,即ak>0. 若ak+1≤0,则 ln(1+an+1)≤0, an+1(1+an+1)+ln(1+an+1)≤0, 与假设矛盾,故ak+1>0,于是当n∈N*时,an>0,因此 即 an>an+1. 综上可得0 当0 从而 于是 变形得 anan+1≥2an-4an+1. 又 得 从而 anan+1<2(an-an+1). 综上可得2an-4an+1≤anan+1≤2(an-an+1). 3)由第2)小题得 由不等式的右端可得 从而 由不等式的左端可得 即 从而 即 参 考 文 献 [1] 中华人民共和国教育部.普通高中数学课程标准[S].北京:人民教育出版社,2003. [2] 杨苍洲.2015年高考湖北文科卷压轴试题的命题手法探究[J].中学生理科应试,2017(4):2-3.2 命题方法探究
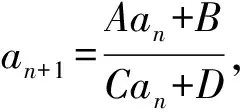

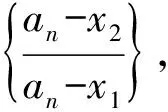
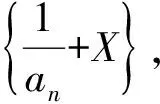




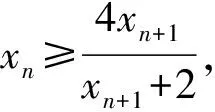
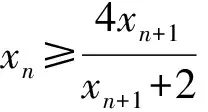





3 命制新题








