数学素养在数学课堂上的养成与体现*——“圆锥曲线的统一定义”教学设计与反思

●

(南通大学附属中学,江苏 南通 226000)

笔者有幸开设了一节“圆锥曲线的统一定义(第一课时)”的公开课，收获良多，既有教学的新发现，又有很多不足，特总结出来，以求得共鸣.

1 背景分析

1.1 教材内容解析

所用教材为苏教版普通高中课程标准实验教科书《数学(选修2-1)》,本节课为第二章第2.5节“圆锥曲线的统一定义”.圆锥曲线在现实世界、社会生活中有着广泛的应用，因此圆锥曲线是一个很重要的数学模型.本章先从整体上认识圆锥曲线概念，了解椭圆、双曲线、抛物线的内在关系，再通过统一定义从总体上进一步认识3种圆锥曲线的关系.本节课从抛物线的定义出发，类比、猜想得到圆锥曲线的统一定义，由特殊到一般符合学生的认知发展规律，使学生感受数学的内在的、和谐的美，并且通过对研究过程的反思，培养欣赏美、发现美的能力和意识，提高数学审美能力.

1.2 学情分析

前面学生已研究了3种圆锥曲线的几何性质，并建构了研究3种曲线的方法体系，本节课将通过对3种圆锥曲线的共同特性的研究建立统一的定义，从知识上完善圆锥曲线的定义，从研究方法上系统领会解析几何的研究思路.笔者所任教班级是理科普通班，表面上学生对3种圆锥曲线的了解有了一定的基础，但在深层次的领悟与归纳上存在欠缺，因此本节课笔者想让学生在“特殊到一般、猜想后再证明思想方法”下培养数学素养，养成良好的思维习惯.

1.3 教学目标

根据本节内容在教材中的作用和地位，教学目标设定如下：

1)了解圆锥曲线的统一定义；

2)理解圆锥曲线的准线的概念，掌握标准方程下的圆锥曲线准线方程；

3)经历类比联想、特殊到一般、转化化归、分类讨论、数形结合、猜想再证明的数学思想，体会深度学习数学的方法；

4)通过小组合作学习的探究过程提升发现、归纳解决问题的能力.

1.4 教学重点

圆锥曲线统一定义的生成、理解、应用.

1.5 教学难点

圆锥曲线的统一定义的生成.

2 教学实录

师：我们已经认识了抛物线，请同学说说抛物线的定义？

生1：平面内到定点F的距离和到定直线l(其中点F不在直线l上)的距离相等的点的轨迹是抛物线，定点F叫焦点，定直线l叫准线.

设计意图由抛物线定义作为新知识生长点、温故知新的同时，发现、探索更深层次的知识，培养学生类比迁移的数学素养.由于问题比较抽象，学生感到无从思考，这时不妨从特殊情况入手，举一特例让学生感知.

师：你对自己的结果有什么发现？

设计意图通过特例让学生感知，形成初步的感性认识，让学生感受到初尝成功的喜悦，获得一定的满足感.

师：这是偶然的巧合还是必然的结论？我们不妨再借助几何手段研究一下.

(教师用几何画板演示动态的轨迹.)

设计意图培养学生对直观观察得到的表象进行质疑、存疑.

学生发现结论：当比值m∈(0,1)时，点P的轨迹像椭圆(如图1)；当比值m∈(1,+∞)时，点P的轨迹像双曲线(如图2).

图1 图2

设计意图给学生反思的时间，让学生思维加以提升.通过几何画板直观手段观察、思考、概括,得出初步的猜想结果.

师：先来讨论第一种情况：m∈(0,1).直观感觉是椭圆,暂且当作椭圆，如果是椭圆，那么定点会是什么点？

生3：焦点.

师：比值会是什么？

生4：离心率.

师：定直线会是哪条直线呢？如何用a,b,c来表示这条定直线呢？

设计意图让学生类比，大胆猜想，不断提出自己的主张、想法.充分发挥小组协同作战的团队精神，完善已有的方法、过程，由此主观能动性得以较好体现.

(学生思考.)

(学生小组讨论.)

师：说说你们为什么选取这些点？

生8：因为特殊——坐标特殊.

师：很好，有时候特殊化，思路会豁然开朗，柳暗花明.

设计意图通过小组讨论发挥学生的主观能动性，学生通过大胆探索、主动求知，争相展示自己的见解，不乏新的想法，使这节课达到高潮，显示了思维的广阔，达到学生的最近发展区.

生9：定义PF1+PF2=2a.

师：定点F1和F2分别是什么？你能验证PF1+PF2=2a吗？

生10：不能验证.

师：大家的想法是好的，但是思路似乎受阻了，怎么判断曲线为椭圆呢？

(学生思考中……)

师：华罗庚先生说过：数缺形时少直观，形少数时难入微.形要靠数来帮忙.

生11：可从轨迹方程形式入手.

师：你有办法证明你的猜想吗？

(学生板演，教师投影.)

解设点P(x,y)，根据题意可得

化简得 (a2-c2)x2+a2y2=a2(a2-c2).

令a2-c2=b2，上式可化为

设计意图通过猜想再证明，这是发现新命题的重要手段，也是引领学生从感性认识上升到理性认识的必经之路，促使学生的思维更具深刻性、系统性.

师：以上从理论角度证明了我们的猜想.如果将条件“a>c>0”改为“c>a>0”，点P的轨迹又如何变化呢？

(教师投影展示学生的运算结果.)

化简得(a2-c2)x2+a2y2=a2(a2-c2),令a2-c2=-b2，上式可化为

设计意图双曲线的类似命题由学生思考、发现，从而引导学生建立圆锥曲线的统一定义，学生的类比迁移能力得到较好展现.

师：从刚才的两个问题中你能总结出什么结论？

圆锥曲线的统一定义平面内到一个定点F的距离和到一条定直线l(其中点F不在直线l上)的距离的比等于常数e的点的轨迹：当01时，它表示双曲线；当e=1时，它表示抛物线.其中e是圆锥曲线的离心率，定点F是圆锥曲线的焦点，定直线l是圆锥曲线的准线.

师：对于焦点在y轴上的椭圆和双曲线的准线方程又如何呢？

设计意图通过对椭圆、双曲线定义的概括，以及对已有的抛物线的定义有了充分感性认识基础上，自然得到了圆锥曲线的统一定义.

师：下面检验同学们所学的成果，请思考如下问题.

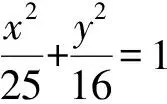
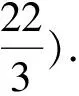
师：通过结合圆锥曲线第一定义和第二定义来解决问题可以看出，我们在解决圆锥曲线的问题时，从定义的角度出发是一种很好的解题思路.

设计意图巩固所学知识，理清知识脉络，结合第一、第二定义综合解题，整合知识的联系与契合.

师(回顾小结)：通过本节课的学习，你有哪些收获？

生(众)：得到了圆锥曲线的统一定义，巩固了先猜想再证明、特殊到一般、数形结合、转化化归、分类讨论和类比联想等思想方法.

3 教学评价

本节课极具探究性和研究性，全面落实以学生为本的教育理念，学生参与度高，真正体现了学生是课堂的主人，又体现出教师的主导地位.教师精心设计，探究自然，将核心问题抛给学生：当比值不为1时，如何研究轨迹，并让学生主动探索准线，在探索定直线的过程中花了近20分钟，是很有必要的.接着在假设的基础上，先判断是否为椭圆，再证明结论，与学生的思维过程相符，比较完整，完成了教学目标.数学核心素养包含数学抽象、逻辑推理、数学建模、数学运算、直观想象、数据分析等6个方面.数学教学活动又是数学核心素养培养的主要途径，因此这节课在不知不觉中培养了学生的数学素养.