习题教学中落地数学核心素养*——圆锥曲线二轮复习的教学与反思

●

(镇海中学,浙江 宁波 315200)

在二轮复习的课堂中，提高习题教学的质量非常重要.《普通高中数学课程标准(2017版)》指明了构建高效课堂的方式：把握数学本质、启发思考、改进教学.

美国数学家哈尔莫斯曾说过：问题是数学的心脏.因此，在习题教学中应注重选择合适的问题，引领复习方向，承载复习内容，通过抓住问题的本质，建立知识之间的关联，达到加强学生的解题能力、提升学生的数学思维能力之目标.习题教学的效率某种程度上决定着高考复习质量的高低，影响着高考的成败.但在习题教学的具体实践中，还是有不少教师信奉“题海战术”兼灌输式讲授，这样非但不能提升学生的解题能力，久而久之还会挫伤学生的学习积极性，使学生产生厌学情绪，出现简单题不肯做、难题又不会做的情况.

笔者一直在探寻高效的习题教学之路，让学生能在潜移默化中提升数学核心素养.本文以二轮复习中”圆锥曲线复习课“为例，谈谈如何渗透数学核心素养，提升学生的思维能力，杜绝学生在解题中出现“只会埋头拉车，却不抬头看路”的糟糕现象.

1 教学过程

1.1 复习回顾

师：同学们经历了圆锥曲线的一轮复习，也做了不少题目，大家到底学了哪些知识？

(学生各抒己见，教师进行总结.)

师：我们学到的知识有：1)曲线分类;2)曲线的性质;3)性质应用.基本的研究思想是用代数研究几何，而最常用的方法是设点法和设线法，并借助韦达定理解决问题.我们不仅可以从定义上区分曲线，还可以从曲线的性质上加以区分.比如教材中提到的光学性质，该性质有怎样的几何特征？

设计说明在复习回顾中，与学生一起梳理圆锥曲线的知识结构与体系，厘清基本思想与常用方法，掌握概念的内涵和外延，使知识的展开不再是无源之水、无本之木，提高习题教学的效率，同时发展学生数学抽象的核心素养，引领学生学会学习，养成良好的学习习惯.

生1:从椭圆一个焦点出发的光线经反射后聚焦于另一个焦点，而双曲线反射后发散，其反向延长线过另一个焦点，经抛物线反射后平行射出.

师：这些性质均与焦点有关，体现了圆锥曲线的统一美，但它们也有差异性，分别为聚焦、发散、平行.再看它们的这些反射面，表现为圆锥曲线的切线，那么这些切线又有怎样的性质呢？

生2:由曲线外的某定直线(准线)上一点出发引曲线的两条切线，则切点弦必过定点(对应焦点)，反之亦成立.

师：这个性质在图形中的体现非常优美，因此同学们留下了较深的印象.我们对这类性质的理解越深、对图形的分析越透，对我们的解题就越有帮助.

1.2 引例示范

例1已知抛物线C的方程为x2=4y，F为其焦点，过不在抛物线上的一点P作此抛物线的切线PA，PB，点A，B为切点，且PA⊥PB.

1)求证：直线AB过定点；

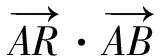
(2018年浙江省宁波市高三数学期末试题第21题)

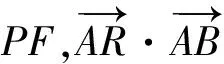
生3:可以先求出点R的坐标，然后进行表示.

师：直译目标，但不简便，能否简化问题？

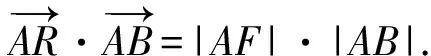
师：很好！还能进一步简化吗？

生5:由PA⊥PB，PF⊥AB，根据射影定理可转化成|PA|2.

师：非常好！抓住图形的几何特征，回归问题的本质，将问题转化成更简单的形式：过抛物线x2=4y上一点A作切线与准线y=-1交于点P，求|PA|2的最小值.有了知识的沉淀，学会欣赏图形之美，就可以启发我们思考，引领解题方向.

设计说明以学生考过且不理想的问题作引例，不仅能拉近与学生的距离，还能引起学生的共鸣，从而启发解题思考，转化问题，简化运算，提高解题效率.同时突出主题，注重几何图形对解题的引领作用，在解题中遇到瓶颈之时，应当回归本质，分析图形，获取思路，突破瓶颈.

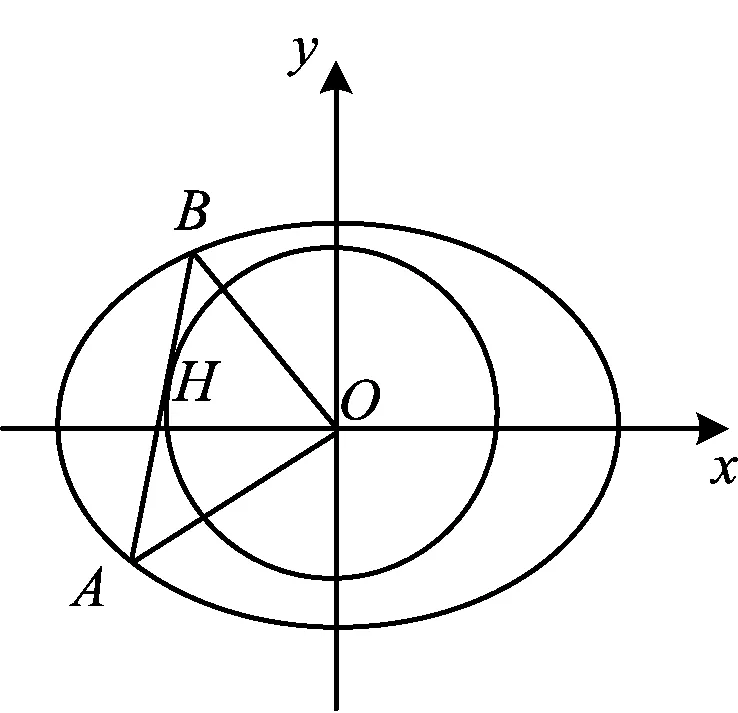
图1

1.3 例题探究

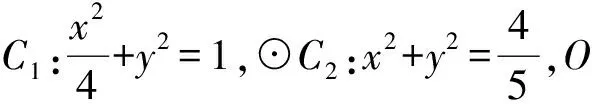
师：请同学们梳理下解题思路.

生6:设直线得参数关系→联立椭圆方程→表示距离并消元→代入韦达定理建立目标函数,求最值.

师：思路很清晰，但计算令人崩溃，可否简化呢？

生7:根据图形猜测OA⊥OB，可用数量积验证.

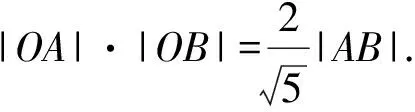
师：以上是间接用k，m表示相切和长度，可否考虑寻找|OA|,|OB|的直接关系呢？请大家以小组为单位进行探究.

设计说明数学探究是课堂教学活动的重要形式之一，是培养学生独立思考能力的重要方式，是提升数学核心素养的重要载体，也能体现学生的主体作用.因此，设计能使学生全面参与的数学探究活动可激发学生自主学习兴趣，调动学生学习的积极性.在师生互动和生生互动的过程中，教师适时地加以点拨，让学生切实参与到知识的发生与发展中，形成适时的思维碰撞，有助于学生理解知识，同时可向学生渗透直观想象的数学核心素养.

1.4 合作交流

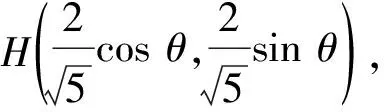
设计说明解决数学问题需要一定的解题经验为依托，这就需要学生在平时注重反思内化.教师将问题设计在学生的最近发展区，让学生体会用数学的乐趣，感受数学知识各部分之间的联系，同时养成良好的数学学习习惯，这不仅符合数学课程标准的要求，而且发展了运算、数据分析等数学核心素养.

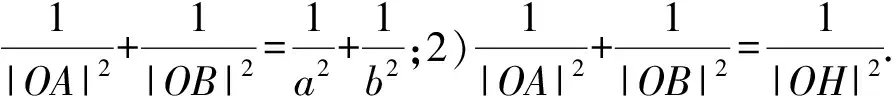
因此有线索指向可先证OA⊥OB.

证明如图2，过点O作CD⊥OA，联结AC,AD，并作OH1⊥AC于点H1，OH2⊥AD于点H2.因为CD⊥OA，所以

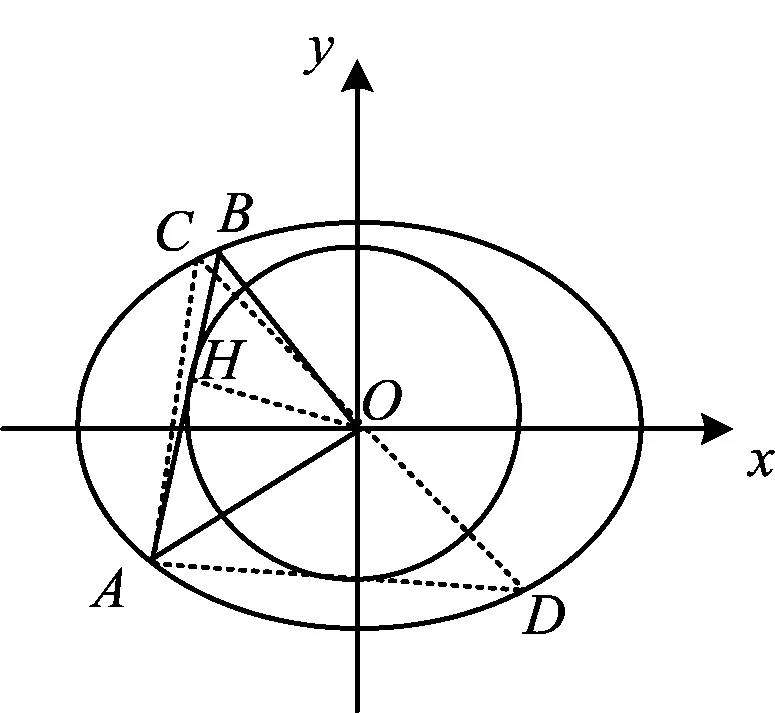
图2

从而AC,AD为⊙O的两条切线，点B必与点C或点D重合,因此OA⊥OB.

生9:例2转化成了二元最值问题，可利用函数思想解决问题.

1.5 总结提炼

师：在今天的课堂上你有什么收获呢？

(学生们阐述自己的课堂收获.)

设计说明层层递进式的设计将一个繁琐的运算问题，通过几何特征的挖掘，逐步转化为学生所熟悉的问题模型，这不仅增强了学生解决问题的信心，培养了数学学习的兴趣，还让学生掌握了圆锥曲线问题的研究方式：代数研究几何、几何辅助代数.学生通过亲身经历，切身体会了优美的图形对解题的帮助，对“欣赏图形之美，启发思考，引领方向”有了更深刻的认识，同时提高了学生的解题能力，进一步落实了直观想象的数学核心素养.

2 教学反思

习题教学是数学教师必须要面对的课题，尤其是在高三的二轮复习中.如何在枯燥的习题讲评中让学生获得一点新的感悟，让学生在解题中有种豁然开朗的感觉，需要我们教师去精心设计课堂环节，不断探索习题教学的高效方式，争取让学生在不知不觉中发展数学核心素养.

2.1 发展数学核心素养重在促进学生学会学习

俗话说：“授人以鱼，不如授人以渔.”教师在教学过程中不仅要传授学生学习经验，加强学习指导，还应积极探索多样化的教学方式，倡导独立思考、动手实践、自主探索、合作交流等学习方式.当解题遇阻时，引导学生重新回到图形，认真审视条件，启发思考，引领解题方向.当遇到美妙的性质与图形关系时，点拨学生及时地体会和理解，促进学生提升对问题的认识高度，而不只是就题论题，限制想象空间，只有会当凌绝顶，才能一览众山小.同时应该提高作业质量，提升学生作业的时效性和自主性，及时解决和整理其中的问题，做学习的主人.这样就能在平时不断提升并充实自我，最终发展数学核心素养.

2.2 发展数学核心素养重在促进学生获取思路

数学解题的推理和运算，实质都是转化与化归，方向都是化繁为简、化抽象为具体、化未知为已知.思路的获取需要在条件和结论中架起桥梁，而我们能做的只能是通过分析题目的已知与待求之间的差异，并努力消除这些差异，从中落实数学核心素养.获取思路具体要经历4个步骤：理解题意、提取信息、联系旧知、重组结构.理解题意是解题的基础，决定着解题方向，决定着能否提取到有效的信息.当学生在解题中遇到瓶颈之际，我们应该提醒学生回归题设，包括数量关系、图形关系以及一些隐性的关系，从中获取启发，进而联系旧知，实现重构，突破难题.掌握了思考的方式，学生就能直面问题，不断探索，进一步认识数学，发展数学核心素养.

2.3 发展数学核心素养重在促进学生反思内化

在数学学习过程中，反思是实现新旧知识相互交融、互相比较的有效途径，是学生提升思维最有效的方法.因此，反思内化是发展数学核心素养的关键环节，在课堂教学中不仅要让学生知道问题是怎么解决的，更要知道是怎么想到这个解决办法的，以便学生在反思中对分析问题、解决问题有更深入的认识，这样才能逐步学会用数学的眼光观察世界、用数学的思维思考世界、用数学的语言表达世界.经常进行多层次的反思内化，是对知识框架的重新架构和再次完善，能使所学知识由“会”到“懂”再到“悟”，直到最终的“活”，才能让学生知其然，知其所以然，更知何由以知其所以然.

2.4 发展数学核心素养重在促进学生整体把握

回归概念和定义，厘清知识的来龙去脉，是解题的保证，也是提升解题能力的利器.离开了知识的整体结构谈数学核心素养就成了无稽之谈.不少学生的数学知识是碎片化的，缺少必要的整合，这就需要教师在教学中分析知识点的内在联系，给学生示范知识的梳理，促进学生理解基本知识、掌握基本技能、体会基本思想、积累数学活动经验，这样才能让数学核心素养扎根于课堂.因此，在复习教学中，教师应当帮助学生厘清各知识点在整个高中数学学习中的地位与作用，与此同时，挖掘教学内容之间的内在联系，培养学生系统的思维习惯.

参 考 文 献

[1] 王开林.让数学核心素养根植于课堂——“指数函数”的教学与思考[J].中学数学教学参考，2017(11)：10-13.

[2] 范东晖.入乎其内，出乎其外——让习题教学更有效[J].中学数学教学参考，2018(11)：47-49.

[3] 郑花青.回归本质：从解题教学谈高考复习[J].中学数学教学参考，2017(10)：56-58.

[4] 张彬，於有海.反思：优化解题思路，简化解题过程[J].中学数学教学参考，2018(3):57-60.