细研教材 整体架构 领悟本质 提升素养*——由两道立体几何题测试结果引发的思考

●

(灵璧第一中学,安徽 灵璧 234200)

1 问题提出

笔者所在学校高二年级近期安排了阶段考试(内容为《数学(选修2-1)》)，学生交出的答卷惨不忍睹，结果触目惊心.教师一天到晚备课、上课、辅导等，教学不留余力，学生不分昼夜记录、模仿、练习、思考等，学习废寝忘食.辛勤的劳动换来的却是微薄的收获，岂不令人心灰意冷、心生倦怠？为什么会出现如此现象？我们又该如何应对？本文以其中的两道立体几何试题为例，谈谈笔者对相关问题的理解，不足之处，敬请批评指正.

2 案例剖析

例1在正方体ABCD-A1B1C1D1中，M是AC的中点，点N是线段DD1上的动点，直线MN与平面ACB1的夹角为α，则cosα的取值范围是

( )

本题为全卷的第12题(选择题压轴题)，总分5分，全年级平均得分1.68分.与学生交流得知：少数学生一看到动态问题就头脑发懵、心慌意乱，只能凭借感觉进行选择；部分学生通过点N分别与点D，D1重合这两种极端状态，利用坐标法并结合选项得出正确答案(或错选B)；多数学生认为平面直角坐标系中直线MN的方向向量与平面ACB1的法向量夹角的余弦值就是所求答案，功败垂成、功亏一篑；得出正确答案的大部分学生采用下文解法1，耗时费力，事倍功半.

解法1不妨设正方体ABCD-A1B1C1D1的棱长为2(下同)，以A为坐标原点、以AB，AD,AA1所在直线为x,y,z轴建立空间直角坐标系A-xyz，则A(0,0,0)，C(2,2,0)，B1(2,0,2)，M(1,1,0)，N(0,2,t)(其中0≤t≤2)，从而

由0≤t≤2，得

r=t-1∈[-1,1]，

于是

当r=0，即t=1时,

cos2α=0，

故

cosα=0.

当r∈(0,1]时，

故

当r∈[-1,0)时,

故

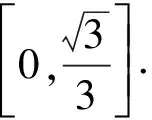
解法2(上同解法1)

解法3如图1，由三垂线定理可知BD1⊥平面ACB1，可证平面BDD1B1⊥平面ACB1，且平面BDD1B1∩平面ACB1=B1M.当N为线段DD1的中点时，MN⊥平面ACB1，此时cosα=0.作DH⊥B1M于点H,D1G⊥B1M于点G,则在Rt△DMH中，

在Rt△D1MG中

结合选项可知答案为A.

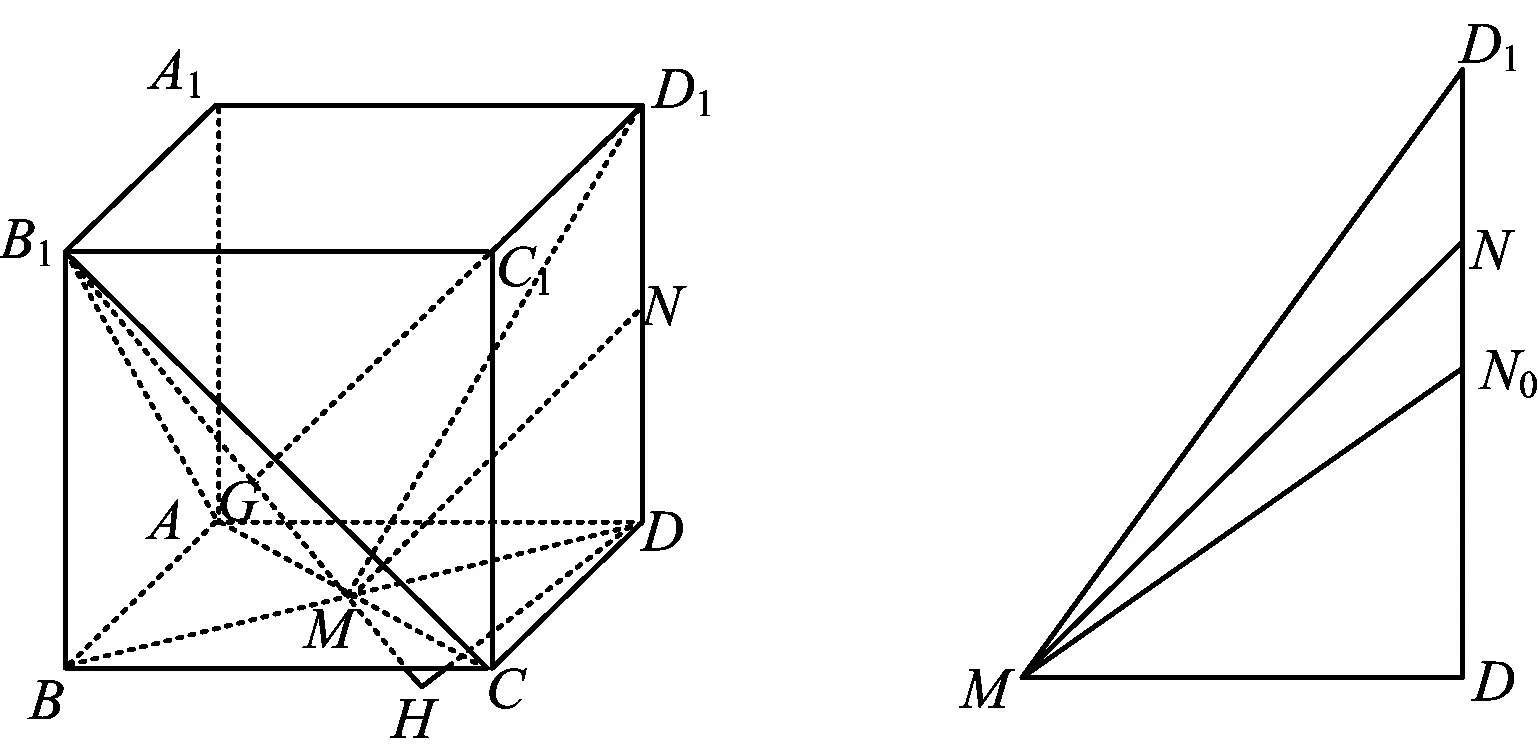
图1 图2

解法4(上同解法3)

取线段DD1的中点N0，则MN0⊥平面ACB1(如图2)，则

cosα=sin∠NMN0.

当点N与点N0重合时,

cosα=sin∠NMN0=0；

当点N与点D重合时,

当点N与点D1重合时，在△N0MD1中，由正弦定理可得

评注空间的角包括直线与直线所成的角α、直线与平面所成的角β、平面与平面所成的角γ(不同于二面角).它们由构成图形的两个要素的方向来决定，而与这两个要素的具体位置无关.空间两条直线s1,s2的“方向”用其方向向量s1,s2来表示，可得cosα=|cos|；两个平面m1,m2的“方向”用该平面的法向量n1,n2来刻画，根据定理(在平面内，如果一个角的两边与另一个角的两边分别垂直，那么这两个角相等或互补)可得cosγ=|cos|；直线s(其方向向量为s)与平面m(其方向向量为n)所成的角满足sinβ=|cos|.一些学生不清楚为什么要用直线的方向向量、平面的法向量来表示直线、平面的“方向”，对空间的角概念的抽象过程认识模糊，结论死记硬背，套用公式生吞活剥，张冠李戴在所难免.

例1的解法1与解法2为坐标法，通过空间直角坐标系将其标准化，无需找出线面角，对空间想象能力要求不高.只不过解法1更聚焦目标cosα，尝试以静制动，利用复合函数单调性求解，求解过程中遭遇到r的符号不定(正号、负号和0)，需要分类讨论，过程繁杂(若学生学习了导数，利用导数法可优化解题过程).解法2利用同角三角函数的关系，保持s始终为正，优化了解题过程.解法3与解法4着眼于直线与平面所成角的定义，将立体几何问题平面化.解法3根据选择题的特点，利用特殊与一般的关系从几种特殊状态下的结论进行逻辑推理判断，事半功倍.解法4利用直线与平面所成角的定义将其转化为平面问题，在隔离出来的平面图形中借助正弦定理与角度变化的连续性对结论进行了完整而严密的推证，是解法3的升级版.学生遇到动态问题信心不足，表象是心理素质不过硬，其深层原因是基础不牢，思维无序.学生错选B，表明其对线面角的形成、发展过程体验不到位，抽象能力差，失分的结果看似令人惋惜，实则是对其学习能力的准确回馈.

图3

例2如图3，平行六面体ABCD-A1B1C1D1的底面ABCD为菱形，∠A1AB=∠A1AD=∠DAB=60°，且A1A=AD=1.

1)求AC1的长；

2)求证：AC1⊥平面A1BD；

3)求三棱锥B-A1C1D的体积.

本题为全卷的第21题，总分12分，全年级平均得分1.82分.多数学生尝试建立空间直角坐标系将几何问题代数化，主要的建系错误为：以D为坐标原点、以DA，DC,DD1(DA1)所在直线为x,y,z轴建立空间直角坐标系D-xyz，其中后一种建系方式可能受到试卷提供的图的影响.

则

2)因为

即

AC1⊥BD.

同理可证

AC1⊥A1B，

又A1B⊂平面A1BD，BD⊂平面A1BD，A1B∩BD=B，故AC1⊥平面A1BD.

得点C1到平面A1BD的距离为

又△A1BD是边长为1的等边三角形，从而三棱锥B-A1C1D的体积为

分析21)由∠A1AB=∠A1AD=∠DAB=60°，知点A1在平面ABCD中的垂足H落在直线AC上.由最小角定理cos∠A1AB=cos∠A1AH·cos∠CAB，得

图4

如图4，以AC与BD的交点O为坐标原点、以OB，OC所在的直线为x，y轴建立空间直角坐标系，则

于是

3)设平面A1C1D的法向量为n=(x,y,z)，则

故三棱锥B-A1C1D的体积为

评注少数学生认为向量法就是向量坐标法.实际上向量法应包括向量基底法和向量坐标法，使用向量基底法的前提条件是已知构成空间(平面)向量的(一组)基底的基向量的模及它们之间的夹角，而使用向量坐标法的前提是条件中具备空间(平面)向量的一组单位正交基底.即前者是根本大法，是后者的根基；后者是前者的特殊情况，是特定统一标准下的向量运算.学生不了解它们之间的逻辑关系，就无法看透问题的本质，解题时盲目类比迁移出错不足为奇.

3 教学思考

3.1 细研教材,整体谋划

教学要处理好教什么(教学内容与教学深度)与怎么教(教学方式)的问题.教材是教师教学和学生学习的素材，理应在教与学中发挥中流砥柱的作用.“知己知彼，方能百战百胜”，只有研习了小学与初中、高中、大学(低年级)的数学教材，才能做好教学的衔接，即及时做好高中教与学需要内容(知识、思想方法等)的铺垫，平稳修完高中数学后还要“扶上马送一程”.数学是一个有机的整体，教学只有基于学科整体，统整所学，将其熔融铸为一体，才能真正发展核心素养.

如《数学(选修2-1)》第二章“空间向量与立体几何”的内容安排基于《数学(必修2)》第一章“立体几何初步”与《数学(必修4)》第二章“平面向量”.教师要弄清每部分内容安排的脉络、重点、难点以及它们之间的联系，教学时才能抓住关键点，做足必需的铺垫.如《数学(必修2)》第一章从空间几何体的整体入手，观察、认识空间立体图形；再以长方体为载体，直观认识和理解空间点、线、面的平行与垂直的位置关系；然后对有关平行、垂直的性质与判定定理用数学语言进行严格表述，对性质定理进行论证；最后给出一些简单几何体的表面积和体积的计算方法.教学中要让学生通过经历直观感知、操作确认、思维论证、度量计算等阶段培养和发展学生的空间想象能力、合情推理与演绎推理的能力.

3.2 理解学生，指导学法

现代学习理论研究表明，理解性学习的关键在于构建知识之间的联系，而理解的程度则由联系的数目和强度决定.从这个角度来看，数学理解的本质就是知识的结构化、网络化和丰富联系.学生知识缺乏、视野狭窄、经验不足，导致其课前预习、课堂听课、课后反思等盲目无序,抓不住重点，无法领悟到问题的本质，整体效益不高.“授之以鱼，不如授之以渔”，数学教学不仅要教授知识，而且要培养思维，即教会学生思考.教师是课堂的主导，学生是学习的主体，只有激发学生的主观能动性，才能提高学生学习探究数学的兴趣，进而提升数学学习的效率.教师在强化教学示范作用的同时，深化理解学生在学习中的困难，给予学生有针对性的指导.罗斯福曾说：“失败固然痛苦，但更糟糕的是从未去尝试.”教师要鼓励学生尝试操作、质疑、交流、总结、创新等.

3.3 精心设计，知难而进

学科核心素养是育人价值的集中体现，是学生通过学科学习而逐步形成的正确价值观念、必备品格与关键能力.数学学科核心素养包括：数学抽象、逻辑推理、数学建模、直观想象、运算能力、数据分析.这些核心素养既相对独立、又相互交融，是一个有机的整体[1].学科核心素养的落脚点主要在课堂，高尚的人格才是最高的学问，只要我们热爱学生、倾心教育，就能理解学生的所作所为，急学生之所急，惑学生之所惑，并尝试给出解决方案.如学生为什么会有教辅依赖症？因为教辅试题多而全，与考试题面目更接近.这应引起教师对教材呈现方式、教学方式、命题技术、综合评价等内容全方位的思考并尝试解决，自觉提高自己的教学修养，在教学过程中重道轻术，给学生更多的机会去做，给学生更多的时间去悟.

教师要充分挖掘教材的例题、习题、测试题等教学素材的功能，对接学生的认知，精心设计，降低平台，让学生拾级而上，知难而进.通过精心设计的教学，强化学生对基础知识的理解、解题方法的提炼、数学思想的领悟、整体结构的构建、解题方案的优化等，通过批判性思维深化认知，提高思维的敏锐性、发散性与灵活性等，在较短的时间内能对各种解题方案和策略进行预设、调整、优化等.

教学时要以课程标准、考试大纲等纲领性文件为标杆，不能轻易降低或提高对相关内容的要求，但要循序渐进，谨防一步到位，还要想方设法改进教学方式，使内容更易被学生理解与接受.

参 考 文 献

[1] 中华人民共和国教育部.普通高中数学课程标准(2017年版)[S].北京：人民教育出版社，2018.