三角形等分积周线的探究*
●
(宁波教育学院,浙江 宁波 315010)
0 引言
三角形的等分积周线,即平分三角形面积的同时也平分此三角形周长的直线.2010年浙江省杭州数学中考模拟题中出现了等分积周线[1].由文献[1]知对于特殊的三角形,存在等分积周线.文献[2]借助几何画板对不等边三角形直观地给出了等分积周线的存在性.那么对于任意给定的三角形是否存在等分积周线?若存在,有几条等分积周线?
文献[3]给出了等分△ABC面积的所有直线,满足条件的直线有无数条且将△ABC分为两个三角形或一个三角形与一个四边形,即至少有一个是三角形.因而若直线DE是△ABC的等分积周线,则只能是图1、图2或图3的情形.不妨设|BC|=a,|CA|=b,|AB|=c.
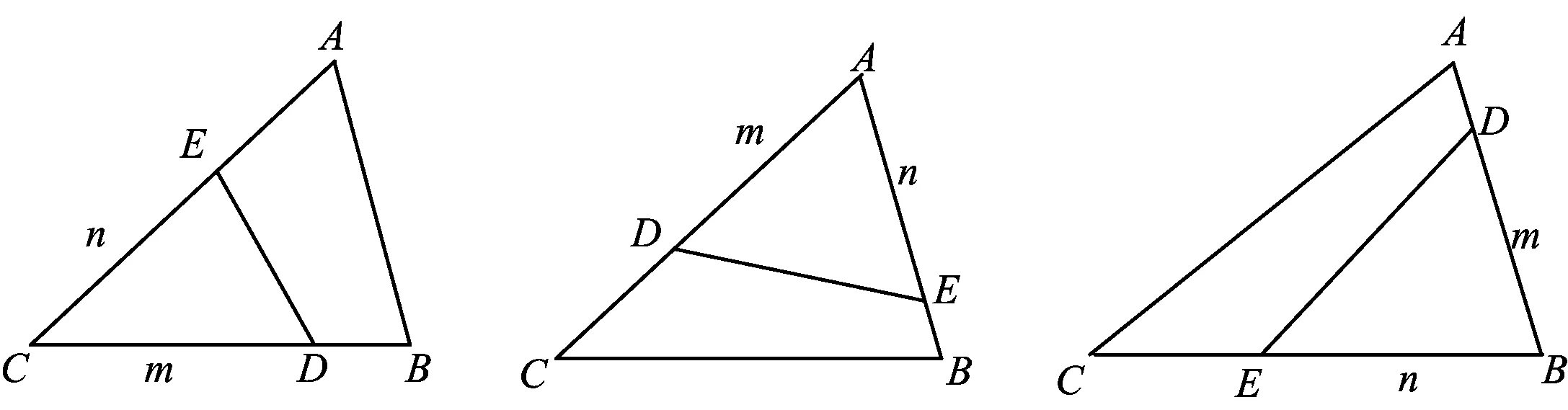
图1 图2 图3
如图1,设|CD|=m,|CE|=n,则由DE平分△ABC的周长得
由DE平分△ABC的面积得
而
且
故
(1)
的两个根.

(2)
的两个根.

(3)
的两个根.
因此,△ABC的等分积周线DE是否存在,只需考虑方程(1)或方程(2)或方程(3)是否有解.
1 等腰三角形
不妨设AB=AC,即b=c.按图1、图2、图3这3种情形加以讨论:
1.1 情形1
若a-2b=0,即
a=2b或a=b+c,
则与△ABC为三角形矛盾,从而Δ>0,于是方程(1)有两个根

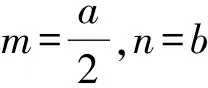


图4
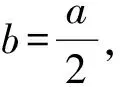
2)若b=a,即△ABC为等边三角形,由图1知此时△ABC的等分积周线为边AC上的中线.

1.2 情形2

当b b(a-b)≤0, 当b>a时, 或 由等腰三角形的对称性,仿情形1类似可得△ABC的等分积周线.综上所述,有: 定理1设△ABC为等腰三角形,且|BC|=a,|CA|=b,|AB|=c,不妨设b=c,则底边BC上的中线为△ABC的一条等分积周线,且 或 综上所述,可得: 定理2设△ABC为非等腰三角形,且|BC|=a,|CA|=b,|AB|=c,不妨设a>b>c,则△ABC有一条等分积周线,且 至此,利用方程(1)~(3)的根给出了三角形的所有等分积周线. 参 考 文 献 [1] 朱宸材.中考“等分积周线”问题浅析[J].中学数学杂志,2012(12):40-41. [2] 王波,游光伟.用几何画板软件探讨三角形等截线问题[J].信息技术,2013(4):187-188,191. [3] 陈咸存.等分三角形面积的直线的可视化探究[J].中学教研(数学),2015(5):27-28.
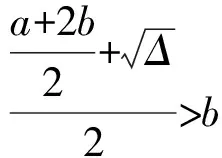



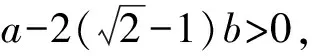
1.3 情形3

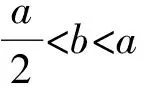
2 非等腰三角形

2.1 情形1

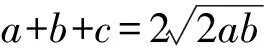


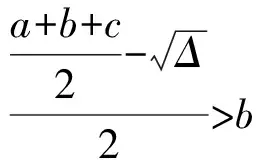

2.2 情形2
2.3 情形3



