常曲率Berwald空间

张纪平，沈晓斌，石擎天

(1.泉州师范学院 数学与计算机科学学院，福建 泉州 362000; 2.福建省大数据管理新技术与知识工程重点实验室，福建 泉州 362000; 3.智能计算与信息处理福建省高等学校重点实验室，福建 泉州 362000)

Antonelli与Matsumoto在文[1]中论述了“Constant-Berwald空间”(下面简称“C-B空间”)的重要性,该空间在物理与生态的发展扮演着重要角色，它不仅应用到物理的“Volterra-Hamilton理论”且最近在生态上有重要新的应用.本文阐明了C-B空间是常曲率Berwald空间并指出射影平坦的Berwald空间是常曲率Berwald空间，重点研究射影平坦的Berwald空间的特征刻划,获得了射影平坦的Finsler空间是Berwald空间的若干个新的充要条件.

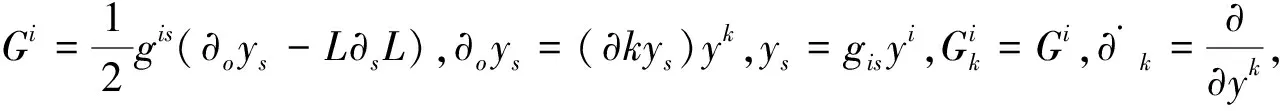
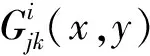
引理1“C-B空间”是常曲率Berwald空间.

从文[2]中(1.14)与定理1.8有

引理2射影平坦的Finsler空间是Berwald空间的一个充要条件是

Gij=0.

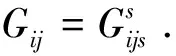
下面研究射影平坦的Finsler空间是Berwald空间的几个新的充要条件.从文[3]中1.5(a)有

(1)

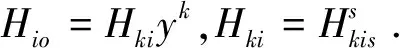
定理1射影平坦的Finsler空间是Berwald空间的一个充要条件是

(n+1)Hi,j=-(N+1)∂jGi-GiGj.

(2)

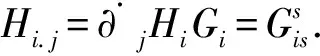
证明对于射影平坦的Finsler空间，从[4]有

(3)

与

(4)

其中：p为射影因子.又

这里-j|k表示j与k对调后两式互减，于是

与

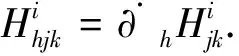
Hij=n∂jpi-∂ipj+(n-1)(pipj+ppij)-∂opij.

上式分别与yi及yj缩并，有

Hoj=∂jp-∂opj+(n-1)ppj,

Hio=n∂opi-∂ip+(n-1)ppj.

从式(1)得

Hi=(n+1)(∂ip+ppi).

(5)

Hi.j=(n+1)(∂jpi+pipj+pipj+ppij).

利用引理2及式(5)知式(2)成立.

反之，由式(5)及式(2)有Gij=0,根据引理2知射影平坦的Finsler空间是Berwald空间.

定理2射影平坦的Finsler空间是Berwald空间的一个的充要条件是

(6)

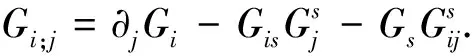
证明显然有

利用式(4)与式(3)知

Pi;j=∂ipj+2pipj+2ppij.

(7)

又Gi=-(n+1)pi关于yi微分,得

功夫不负有心人。经过几年努力，学校艺术生已经占全校学生总数的一半以上，每个年级分别有音乐班、美术班和普通的文化班，学生实现了多元选择、个性发展。学校办学业绩有了显著提高，大部分学生通过参加艺术类高考都能顺利进入大学深造。受到艺术生的感染和鼓舞，文化班的学生也不断进步，录取率逐年上升，他们创造了一个又一个蝶变的奇迹。

Gij=-(n+1)pij.

(8)

从式(7)、(8)与引理2知式(6)成立.

反之，由式(6)～(8)有Gij=0根据引理2知射影平坦的Finsler空间是Berwald空间.

定理3射影平坦的Finsler空间是Berwald空间的一个的充要条件

(n+1)∂kyi=gikG+2yiGk-ykGi.

(9)

其中：G=Gkyk.

证明从文[5]有

gij;k=-2Cijk;o.

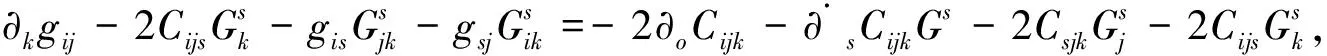
∂kgij=2gijpk+gikpj+gjkpi+yipjk+yjpik+pCijk-2∂oCijk.

(10)

式(10)与yi缩并，知

∂kyi=-2yipk-gikp-ykpi-L2pik.

(11)

当它是Berwald空间时,从引理2有Gik=0,从而(9)式成立.

反之,由式(9)与式(11)得pik=0,借助引理2知射影平坦的Finsler空间是Berwald空间.

从式(10)中及引理2可得推论1.

推论1射影平坦的Finsler空间是Berwald空间的一个充要条件是

(n+1)∂kgij=-2gijGk-gikGj-gjkGi-4GCijk-2(n+1)∂oCijk.

(12)

推论2射影平坦的Finsler空间是Berwald空间的一个充要条件是

(n+1)∂kli=Gilk+Gkli+Glik.

定理4射影平坦的Finsler空间是Berwald空间的一个的充要条件是

(n+1)γiok=-yiGk-ykGi.

(13)

证明显然有

(14)

利用式(12)有

(n+1)γiik=-giiGk-gikGi-yiGik-2GCiik-(n+1)∂oCiik.

(15)

它与yj缩并有

(n+1)γiok=-yiGk-ykGi-L2Gik.

(16)

借助引理2,从式(16)可得式(13).

反之,由式(13)与式(16)可推出Gik=0,利用引理2充分性得证.

从式(15)知推论3成立.

推论3射影平坦的Finsler空间是Berwald空间的一个充要条件是

(n+1)γiik=-giiGk-gikGi-2GCiik-(n+1)∂oCiik.

利用式(4)与引理2又可得

推论4射影平坦的Finsler空间是Berwald空间的一个充要条件是

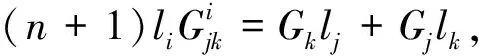
定理 5射影平坦的Finsler空间是Berwald空间的一个的充要条件是

(n+1)Pijk=GCijk+gijGk+gkjGi-(n+1)γijk.

(17)

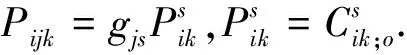
证明从文[5]中有

gij;k=-2Cijk∶o,Cijk∶o=Pijk,

因而

gij;k=-2Pijk.

又

利用式(3)与式(4)得

-2Pijk=∂kgij+2pCijk+gikpj+gjkpi+2gijpk+yipjk+yjpik.

(18)

从式(14)、(18)、(3)与(4)可得

(n+1)Pijk=GCijk+yiGik+gjkGk+gjkGi-(n+1)γijk.

(19)

当射影平坦的Finsler空间是Berwald空间时,从引理2有Gik=0,于是由式(19)可得式(17). 反之,对于射影平坦的Finsler空间,从式(19)与式(17)可推出Gik=0,充分性得证.

另一证明.也可由式(17)与yj缩并可推出式(13)成立.利用定理4可证明该定理.

从文[3]中知射影平坦的Finsler空间是纯量曲率的Finsler空间,又对于Berwald空间有Gij=0,因此文[6]中定理4.5(4)a成立,从而有

定理6射影平坦的Berwald空间是具有常曲率的Finsler空间.

综上，本文给出了射影平坦的Finsler空间是Berwald空间的9个新的充要条件，并证明了射影平坦的Berwald空间是具有常曲率的Finsler空间.