初等函数中常见的概念性错误分析

◎王爱华

数学解题中的错误常有以下几种类型：（一）概念性错误；（二）推理和论证性错误；（三）计算错误、看图和作图错误。其中概念性错误和推理性错误，可以归属于逻辑性错误，而逻辑性错误又可能导致计算错误和图形错误，因此认识数学解题中某些常见的逻辑性错误，并分析其产生的原因对于提高数学教学质量，促进学生的数学解题能力，是很重要的。本文仅就函数概念的有关问题通过一些常见的例子，以分析其概念性错误及原因，旨在教与学的过程中对数学概念的重要性引起足够的重视。

一、函数定义域及表述问题

函数的定义域是“x≠1的一切实数”，这种说法包含了逻辑上的矛盾，因为既然说“x≠1”，就不是“一切实数”，而若是“一切实数”，就应包括x=1。这样说违反了矛盾律。正确的说法，可以表述为“上述函数定义域是满足x≠1的实数全体”，或用区间表示为：“（-∞，1） ∪ （1， + ∞）”， 或 用 集 合 表 示 为： “

二、把文字题翻译成函数式

例如：列式表示以下各题中y与x的函数关系：

（1）某质点在坐标平面上总按“纵坐标y是横坐标x的两倍”的规律运动。

（2）某质点按速度为2（速度单位）作等速直线运动，走过的路程y是时间x函数。

（3）橡皮2角钱一块，买x快，花了y角钱，y是x的函数。

一般地，学生容易将上述三个函数关系式都写成y=2x，其实这三个函数是不同的：（1）y=2x，x∈ （-∞，+∞）；（2）y=2x，x∈[0， +∞ )；（3）y=2x，x∈N（包括0的扩大的自然数集），它们的图像也各不相同，分别如图1（a）、（b）、（c）。

为什么会发生这样的错误呢？这是因为对函数概念理解片面。函数概念有三要素：定义域、值域、对应关系（解析式）。如果把函数仅理解成解析式，就要犯“以偏概全”的错误。

再如图2，某小隧道截面，矩形上接半圆形，已知截面周长为15m，试写出截面面积S关于底宽x的函数式。

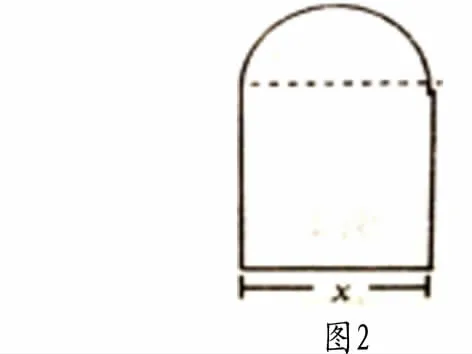
如果解题到此结束，所得结果是不完全的，因此依问题的实际意义，（*）式中的自变量的取值范围是限定的；如果不指出这一点，就可能导致不合理的结果，例如，在（*）式中置x=10，则所求的S是负值，而面积是非负的，所以应该在写出（*）式的同时，把限制条件（定义域和值域的限制）也写出来：S＞0，x＞0。

故所求函数式应是

三、关于函数性质

例 1.设 f（x）=ax7+bx3+cx-5，若已知 f（-7）=7，求f（7）的值。

误解：因为f（x）是x的奇次幂之和，故为奇函数，从而f（7）=-f（-7）=-7

错在哪里？错在f（x）不完全是x的奇次幂之和，因为常数（-5）应视为x的零次幂，而0是偶数，因此f（x）并非奇函数。

正确的解法：令 g（x）=f（x）+5=ax7+bx3+cx，则 g（x）是 x的奇次幂之和，故是奇函数，因而有：g（-x）=-g（x）⇒f（-x）+5=-[f（ x ）+5)⇒f（-x）=-f（x）-10∴f（x）=-f（-x）-10，故 f（7）=-f（-7）-10=-7-10=-17

例2.在2的条件下，求 f（x）=（log2的最小值。

误解：由条件式推得：，从而 -3≤

∵log2x是增函数，∴f（x）的最小值是：

这个结果是错误的，原因是并不能有对数函数的递增性，推出两个对数函数的乘积也是增函数，本题的函数就不是增函数。

事实上，

它是一个关于log2x的“二次函数”。因为a=1＞0，所以f（x）关于log2x有最小值。

正确的解法：在限制条件下得：

当时，有最小值，

以上列举了一些常见例子，分析了函数的概念性错误及产生原因。类似的问题还有很多（诸如“算术根”、“绝对值”等看似简单的概念），这里就不一一赘述。总之，对于数学概念，不论是初学或用之解题，都必须从根本上理解其含义和实质，准确地掌握概念，应用概念，才不至于造成逻辑性错误。