高中数学课堂有效教学的策略探究

◎吴荣沛

“有效教学”的提出为实施新课标注入了活力，那么，何为有效教学？有效教学必须目标有效：清晰、简明；内容有效：适量、适度；教法有效：灵活、恰当；反馈有效：课堂练习、课后作业有效反馈。总之，有效教学是以学生能力形成为宗旨，它一种理念，更是一种策略。

一、有效教学必须基于学习兴趣

苏霍姆林斯基说：“为了使学生在智力上和精神上得到成长，就必需使他们有对知识的渴望和掌握知识的愿望。”然而，“低起点，小步走”更容易激发学习兴趣。

例 高中数学必修1《函数概念》第一课时。

初中函数概念：在某一变化过程中，有两个变量x，y。在某一法则的作用下，如果对于x的每一个值，y都有唯一的值与其相对应，这时，就称y是x的函数。

而高中函数概念是以两个非空数集的间元素的对应来定义的，它与初中的函数概念是有很大的区别，为了让学生更好地理解和掌握定义，在教学中可以这样处理：

①低起点：复习初中函数概念及表示方法。

②小步走：第一步，对概念中“对于集合A中的任意一个数x，在集合B中都有唯一确定的数f（x）和它对应。”的理解。在一对一、多对一，一对多的对应方式中分辨出可以形成函数关系的对应。第二步，f：A→B、y=f（x）都是表示函数的抽象符号，函数具体表示一般通过三种方法：解析式法、图像法、列表法。

如此，所有学生都跟得上，学得了，学习的信心与决心更容易确立。

二、有效教学必须重视过程展示

学生不易吃透数学思想和数学方法，究其原因，是缺少知识形成过程、结论得出的思考，缺乏知识点的动态和综合性连接。因此，有效教学必须充分展示知识的形成、问题解决的过程。

例 设F（1，0），M点在x轴上，P点在y轴上，且。当点P在y轴上运动时，求N点的轨迹C的方程；

解析：由学生自主画图，以转化条件、综合分析条件探究问题解决过程：

综合条件：由 F（1，0），结合（2）、（3）得；故 y2=4x（x＞0）是轨迹C的方程。

题中的分析综合注重基本数学思想的渗透，如数形结合思想、转化思想、综合应变等。课堂上对知识形成过程、解题分析过程的充分展示至关重要。

三、有效教学必须重视问题探究

布鲁纳说：“探索是教学的生命线。”在课堂引导中精心设置，使能力问题化、问题层次化，引导学生善于发现问题和提出问题，真正让学生在课堂中实现数学知识的“再发现”、“再创造”。

例 化简：

先让学生自主分析解答，再归纳总结：

解法1：（从“角”入手，复角化单角）

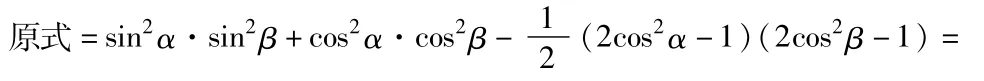
解法2：（从“名”入手，异名化同名）

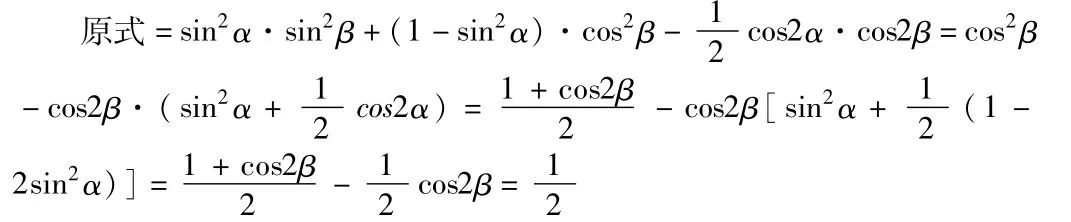
解法3：（从“幂”入手，利用降幂公式先降次）

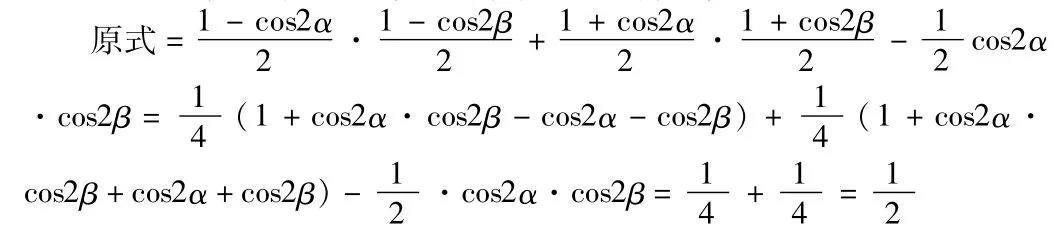
解法4：（从“形”入手，利用配方法，先对二次项配方）

通过以上解法的探究，可以发现：有角的二倍关系，可考虑应用倍角公式；有幂次关系可考虑降幂；函数名称有正弦、余弦，可异名化同名等等.这样的探究，促进了学生的解题能力、学习效率以及课堂效率的提高。

四、有效教学应该让学生在实践中有感悟

学生的底气源自扎实的基础知识和基本技能，而扎实的基础源自实践积累，因此，有效课堂应该让学生在实践中有所感悟，只有学生自己“悟”出的才是最真的、最扎实的。

例 抛物线的顶点在原点，焦点在射线x-y+1=0（x≥0）上

（1）求抛物线的标准方程；

（2）过（1）中抛物线的焦点F作动弦AB，过A、B两点分别作抛物线的切线，设其交点为M，求点M的轨迹方程。

第（1）小题中，学生画出图形后很容易观察得出（0，1）是所求抛物线的焦点。使学生悟出：数形结合是解析几何的核心思想。

第（2）小题解析中设 A（x1，y1），B（x2，y2）得过抛物线上 A、B两点的切线方程分别是，然后联立，解得。设直线AB的方程为y=kx+1，联立x2=4y得x2-4kx-4=0再运用韦达定理有x1x2=-4，进而得），故点M的轨迹方程为y=-1。使学生悟出解析几何的重要解题策略：一是要大胆设点、设线，二是要遇上字母运算要有一算到底的决心。

通过反思，可以知道有效教学追求的就是课堂教学效益的最大化，将课堂变成师生高效发展的课堂，共赢的课堂。高效课堂一定是不让时间虚度一分，不让学生虚坐一个。

《教育的适合性（The Relevance of Education）》——布鲁纳