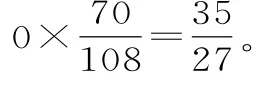2-3总复习过关卷答案与提示
一、选择题
1.B2.D3.C4.A5.C6.A7.A8.D9.C1 0.B1 1.A1 2.D1 3.A1 4.A1 5.B1 6.A17.C1 8.B1 9.B2 0.C2 1.B2 2.C23.C 24.C2 5.B2 6.B2 7.C2 8.B29.B 30.D3 1.D3 2.D3 3.C3 4.B35.A 3 6.B3 7.B3 8.B3 9.A40.B
二、填空题
4 1.3 64 2.24 3.16 8 04 4.74 5.8
46.2 04 7.0.84 8.0.24 95 0
5 1.0.1 7 925 2.1 05 3
5 4.2 5 5.0 0 1
5 6^y.=6.5x-1 05 7.D(3,1 0)58.4.5 1 4
5 9.9 9.5%
三、解答题
6 0.(1)分三步:①先选百位数字,由于0不能作为百位数字,因此有5种选法;②十位数字有5种选法;③个位数字有4种选法。
由分步乘法计数原理知,所求三位数共有5×5×4=1 0 0(个)。
(2)分三步:①百位数字有5种选法;②十位数字有6种选法;③个位数字有6种选法。
故所求三位数共有5×6×6=1 8 0(个)。
(3)分三步:①先选个位数字,有3种选法;②选百位数字,有4种选法;③选十位数字也有4种选法。
所求三位奇数共有3×4×4=4 8(个)。
(4)分三类:①一位数共有6个;②两位数共有5×5=2 5(个);③三位数共有5×5×4=1 0 0(个)。因此,比10 0 0小的自然数共有6+2 5+1 0 0=1 3 1(个)。
(5)分四类:①千位数字为3或4时,共有2×5×4×3=1 2 0(个);②千位数字为5,百位数字为0,1,2,3之一时,共有4×4×3=4 8(个);③千位数字为5,百位数字为4,十位数字为0,1之一时,共有2×3=6(个);④还有54 2 0也是满足条件的1个。故所求四位数共1 2 0+4 8+6+1=1 7 5(个)。
6 1.(1)一个球一个球地放到盒子里去,每个球都可有4种放法,由分步乘法计数原理知,放法共有44=2 5 6(种)。
(2)为保证“恰有1个盒子不放球”,先从4个盒子中任意拿走1个,即将4个球分成2,1,1的三组,有C24种分法;然后再从3个盒子中选1个放2个球,其余2个球对应2个盒子,全排列即可。由分步乘法计数原理知,共有放法=1 4 4(种)。
(3)“恰有1个盒内放2个球”,即另外的3个盒子放剩下的2个球,而每个盒子至多放1个球,即另外3个盒子中恰有1个空盒。因此,“恰有1个盒子放2个球”与“恰有1个盒子不放球”是一回事,故也有1 4 4种放法。
(4)先从4个盒子中任意拿走2个,有种拿法,问题转化为:“4个球,2个盒子,每盒必放球,有几种放法?”从放球数目看,可分为(3,1),(2,2)两类:第一类,可从4个球中先选3个,然后放入指定的一个盒子中即可,有种放法;第二类,有种放法。因此,共有(种)方法。由分步乘法计数原理得“恰有2个盒子不放球”的放法有

6 2.令x=1,则a0+a1+a2+…+a7=-1。①
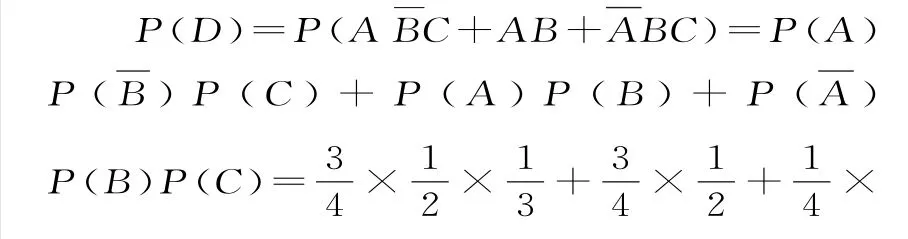
令x=-1,则a0-a1+a2-…-a7=37。②
(1)令x=0,得a0=1,代入①中得:
a1+a2+…+a7=-2。
(2)由①-②得:
2a1+2a3+2a5+2a7=-1-37。
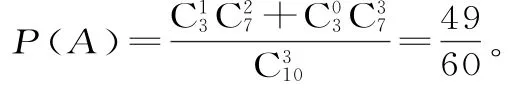
所以a1+a3+a5+a7=所以选出的3名同学是来自互不相同学院的概率为
(2)随机变量X的所有可能值为0,1,2,所以随机变量X的分布列是:-10 9 4。


表1
(3)因为(1-2x)7的展开式中,a0,a2,a4,a6大于零,而a1,a3,a5,a7小于零,所以|a0|+|a1|+|a2|+…+|a7|=a0-a1+a2-a3+a4-a5+a6-a7=37=21 8 7。
6 3.(1)设“选出的3名同学是来自互不相同的学院”为事件A,则:
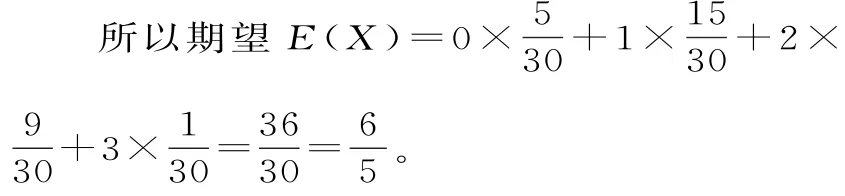
6 4.(1)设事件A表示“甲同学问题1回答正确”,事件B表示“甲同学问题2回答正确”,事件C表示“甲同学问题3回答正确”。则依题意知,记“甲同学能进入下一轮”为事件D,则:(2)X可能取值是6,7,8,1 2,1 3。所以X的分布列为:所以X的数学期望为E(X)=
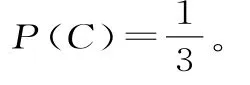

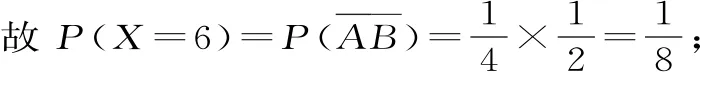
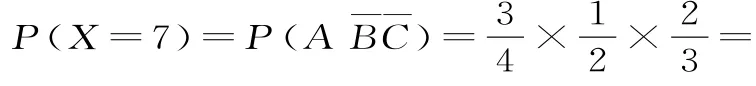




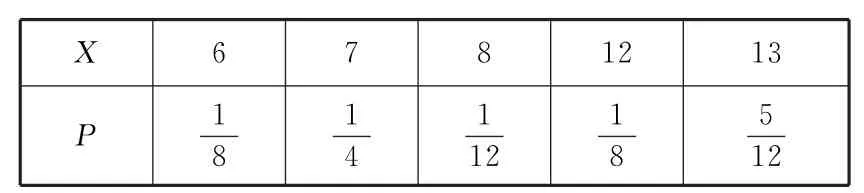
表2

6 5.(1)设报考飞行员的人数为n,前三小组的频率分别为p1,p2,p3,则由条件可得:又因为p2

(2)由(1)可得,一个报考学生体重超过
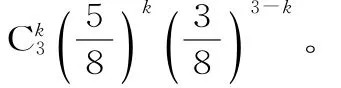
=

表3

6 6.(1)(2)根据列联表中的数据,得到:

表4
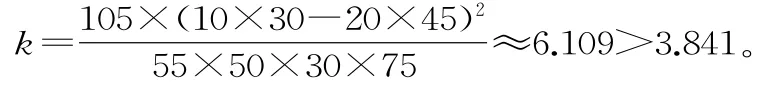
因此有9 5%的把握认为“成绩与班级有关系”。
(3)设“抽到6或1 0号”为事件A,先后两次抛掷一枚均匀的骰子,出现的点数为(x,y)。
所有的基本事件有(1,1),(1,2),(1,3),…,(6,6),共3 6个。
事件A包含的基本事件有(1,5),(2,4),(3,3),(4,2),(5,1),(4,6),(5,5),(6,4),共8个。
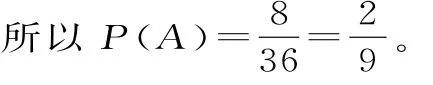
6 7.由题意 X~N(0,22),求得P(X≤4)=P(-4≤X≤4)=0.9 5 44。
设Y表示5件产品中合格品个数,则Y~B(5,0.9 5 44)。
所以P(Y≥5×0.8)=P(Y≥4)=
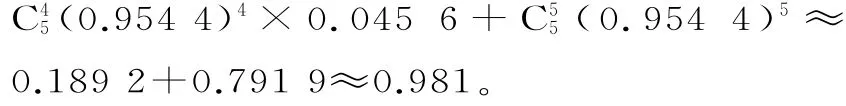
故生产的5件产品的合格率不小于8 0%的概率为0.9 8 1。
6 8.(1)根据表中所列数据可得散点图如图1所示。
(2)列出表5,并用科学计算器进行有关计算:
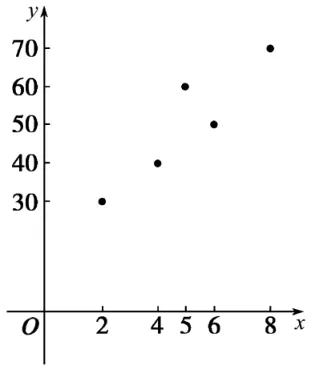
图1

表5
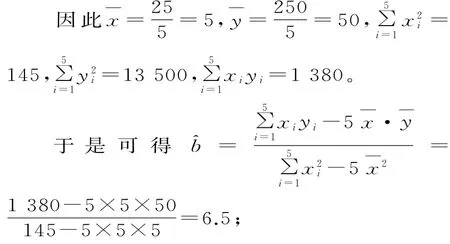
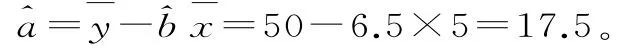
因此,所求线性回归直线方程为^y=6.5x+1 7.5。
(3)根据上面求得的线性回归直线方程,当广告费支出为1 0百万元时,^y=6.5×1 0+1 7.5=8 2.5(百万元),即这种产品的销售收入大约为8 2.5百万元。
6 9.(1)由题可得,抽两次得到的结果3 6种可能,但两次之和为6的可能有:(3,3),(2,4),(4,2),(1,5),(5,1),所以P=5。3 6
(2)由已知可得X的所有可能取值为5,3,1,0。所以X的分布列为:
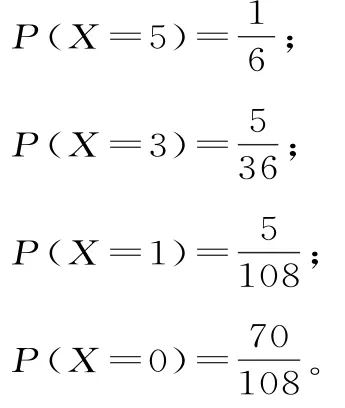

表6