浅淡超几何分布和二项分布的区别与联系

■重庆市铁路中学校 何成宝

一、混淆超几何分布和二项分布的定义而导致错误

我们知道二项分布的定义:一般地,在n次独立重复试验中,设事件A发生的次数为X,在每次试验中事件A发生的概率为p,那么在n次独立重复试验中,事件A恰好发生k次的概率P(X=k)=Cknpkqn-k,其中0＜p＜1,p+q=1,k=0,1,2,…,n,则称X服从参数为n,p的二项分布,记为X～B(n,p)。

超几何分布的定义是:一般地,在含有M件次品的N件产品中,任取n件,其中恰有X件次品数,则事件{X=k}发生的概率

N中m=m i n{M,n},且n≤N,M≤N,n,M,N∈N*,则称X服从超几何分布,记为X～H(n,M,N)。

由以上定义可知,二项分布模型和超几何分布模型最主要的区别在于是有放回抽样还是无放回抽样。一般说来,有放回抽样与无放回抽样计算的概率是不同的,特别在抽取对象数目不大时更是如此。所以,同学们在解有关二项分布和超几何分布问题时,仔细阅读、辨析题目条件非常重要。同学们对这两个模型的定义不能很好地理解,下面就要对含“取”或“摸”的题型加以分析。

例1 口袋中有8个白球,2个黑球,从中随机地连续取3次球,每次取1个,求:

(1)不放回抽样时,取到黑球的个数ξ的分布列;

(2)放回抽样时,取到黑球个数η的分布列。

分析：不放回抽样时,若取出1个,则总体就少1个,因此ξ的最大值为2,属于超几何分布模型。放回抽样时,每次抽取时的总体没有改变且每次取到黑球的概率相同,因此η的最大值为3,属于二项分布模型。

解：(1)不放回抽样时,取到的黑球个数ξ可能的取值为0,1,2,则:

所以η的分布列为:

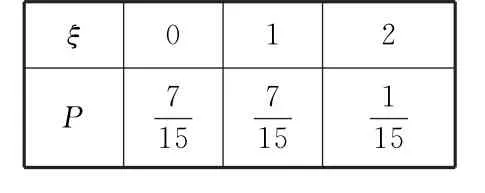
ξ 0 1 2 P 7 1 5 71 1 51 5

(2)放回抽样时,取到的黑球个数η可能的取值为0,1,2,3。又由于每次抽到黑球的概率均为,3次取球可以看成3次独

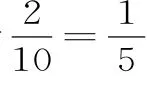
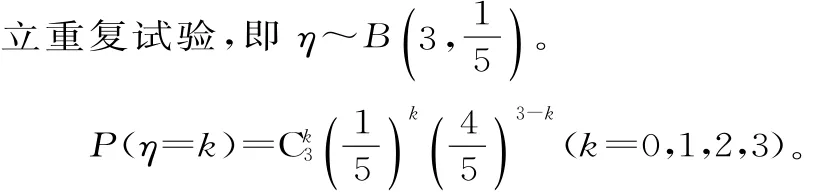
所以η的分布列为:

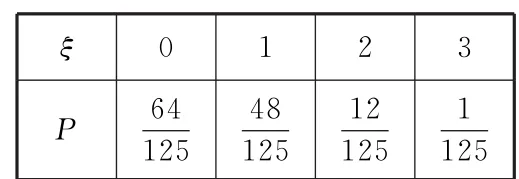
ξ 0 1 2 3 P 6 4 1 2 5 1 4 8 1 2 5 1 2 1 2 51 2 5

点评:两种分布的差别就在于“有”与

涉及超几何分布和二项分布的分布列和期望问题已成为常考题型,不少同学不明白超几何分布和二项分布之间的区别,从而解题错误。因此,有必要阐述一下两者之间的区别和联系。下面举例说明,以供同学们参考。“无”的差别,“放回”和“不放回”就是两种分布转换的关键。

练习：在高二年级的联欢会上设计了一个摸奖游戏,在一个口袋中有大小相同的1 0个红球和2 0个白球。从中随机地连续取5次球,每次取1个,求:

(1)若从中任意摸出5个球,求摸到4个红球的概率;

(2)摸出1个球记下颜色,放回后再摸1个球,反复5次,摸到4个红球1个白球就是一等奖,求获一等奖的概率。

解析：(1)从3 0个球中摸出5个球,共有C530种方法,摸到4个红球有C410C120种方法,摸到4个红球的概率为

(2)有放回摸球,由于每次抽到红球的概率均为,5次取球可以看成5次独立重复试验,设取到红球个数为ξ,则ξ～

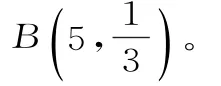
故摸到4个红球1个白球的概率为:

点评:通过此例可以看出,有放回抽样时,每次抽取时的总体没有改变,每次抽到某物的概率是相同的,可以看成是独立重复试验,此种抽样是二项分布模型。而无放回抽样时,取出一个则总体中就少一个,因此每次取到某物的概率是不同的,此种抽样为超几何分布模型。

二、超几何分布和二项分布的联系与区别而导致错误

超几何分布和二项分布确实有着密切的联系,但也有明显的区别。样本个数越大,超几何分布和二项分布的对应概率相差越小,当样本个数为无穷大时,超几何分布和二项分布对应的概率几乎相等。还有超几何分布所涉及的样本数目是具体的。所以只有掌握“有、无放回”及样本个数“有限、无限”时所对应的分布类型,才不会出现选择方法上的错误。

例2 根据我国相关法律规定,食品的含汞量不得超过1.0 0p p m,沿海某市对一种贝类海鲜产品进行抽样检查,抽出样本2 0个,测得含汞量(单位:p p m)数据如表1所示:

表1

(1)若从这2 0个产品中随机抽取3个,求恰有1个含汞量超标的概率;

(2)以此2 0个产品的样本数据来估计这批贝类海鲜产品的总体,若从这批数量很大的贝类海鲜产品中任选3个,记ξ表示抽到的产品含汞量超标的个数,求ξ的分布列及数学期望E(ξ)。

解析：(1)记“从这2 0个产品中随机抽取3个,恰有一个含汞量超标”为事件A,则所求事件概率为:

(2)根据题意,这批贝类海鲜产品中含汞量超标的概率为P=5=1,抽到的产品含2 04汞量超标的个数ξ的所有可能取值为0,1,2,3。

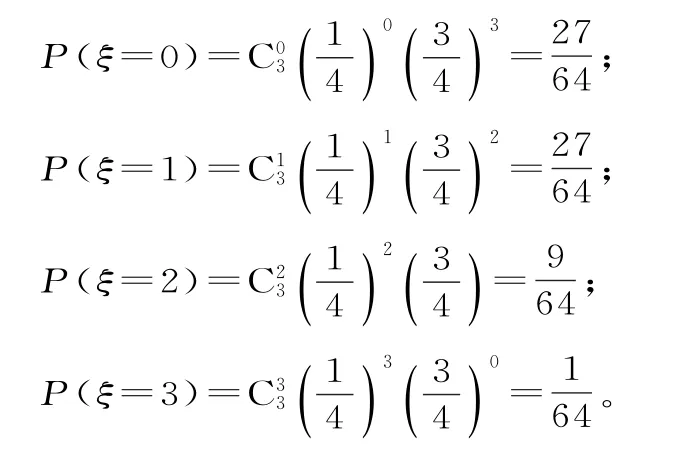
故ξ的分布列为:

ξ 0 1 2 3 P 2 7 6 4 91 2 7 6 46 46 4

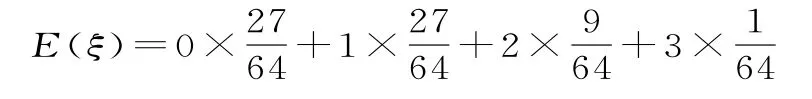
点评:本题第(2)问是二项分布问题,求解时,容易看成超几何分布来处理,造成错解。由二项分布和超几何分布的定义可知,二项分布和超几何分布的区别是“有放回抽样”还是“无放回抽样”。