2-3总复习过关卷

■浙江省海宁中学 徐建平

编者的话：强化对核心考点的演练、注重对经典题型的归纳,是学好数学的秘诀,基于此,本刊编辑部特开设此栏目,希望同学们能认真练习。

一、选择题

1.现有4件不同款式的上衣和3条不同颜色的长裤,如果一条长裤与一件上衣配成一套,则不同的配法种数为( )。

A.7 B.1 2 C.6 4 D.8 1

2.从1,2,3,4,7,9这6个数中任意选出2个不同的数作为对数的底数和真数,则所有不同的对数的值的个数为( )。

A.3 0 B.2 5 C.2 0 D.1 7

3.学校表彰获得先进的同学,现对6位优秀的同学进行合影留念,6位同学站成一排,其中甲、乙、丙3人不能都站在一起的排法种数有( )。

A.7 2 0 B.6 8 4 C.5 7 6 D.1 4 4

4.社会实践活动是高中生必须要经历的一项活动。某校要从4名男生和3名女生中选出4人去参加社会实践,由于某种原因,男生甲与女生乙不能同时参加,则不同的选派方案的种数有( )。

A.2 5 B.3 5 C.8 2 0 D.8 4 0

5.二项式的展开式中的常数项为( )。

A.8 0 B.-8 0 C.4 0 D.-4 0

6.设(x2+1)(2x+1)9=a0+a1(x+2)+a2(x+2)2+…+a11(x+2)11,则a0+a1+a2+…+a11的值为( )。

A.-2 B.-1 C.1 D.2

7.社团活动是最受大学生欢迎的活动,话剧社团拟从含有2名女生的1 0名大学新生中任选3人进行话剧活动满意度调研,记女生入选调研的人数为ξ,则ξ的分布列为( )。

A.

ξ 0 1 2 P 7 1 5 71 1 51 5

B.

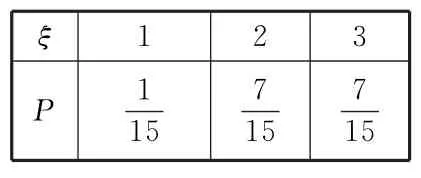
ξ 1 2 3 P 1 1 5 77 1 51 5

C.

ξ 0 1 2 P 1 2 13 16

D.

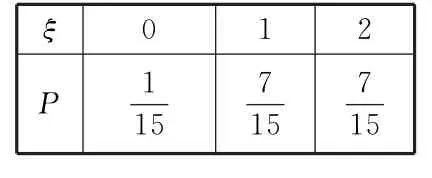
ξ 0 1 2 P 1 1 5 77 1 51 5

8.在5件产品中,有3件一等品和2件二等品,从中任取2件,那么四个选项中概率结

果为的事件是( )。

A.都不是一等品

B.恰有一件一等品

C.至少有一件一等品

D.至多有一件一等品

9.十一国庆长假,甲、乙、丙3人到3个景点旅游,由于行程安排,每人只去一个景点游玩。若设事件A表示“3个人去的景点不相同”,事件B表示“甲独自去一个景点”,则概率P(A|B)的值为( )。

1 0.民航招飞是每年高考前的一项招生活动。某民航公司要从某市应届高中生中选拔一批学生去报考飞行员,通过对报名学生的体检后发现,体型合格的概率为,视力合格的概率为,其他一项标准合格的概率为。现从这批学生中任选一名,则该生三项均合格的概率为(假设三项标准互不影响)( )。

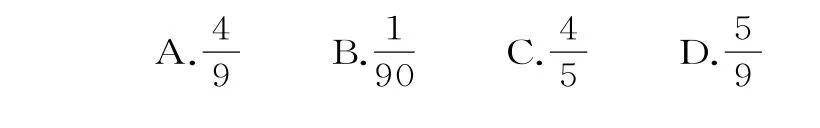
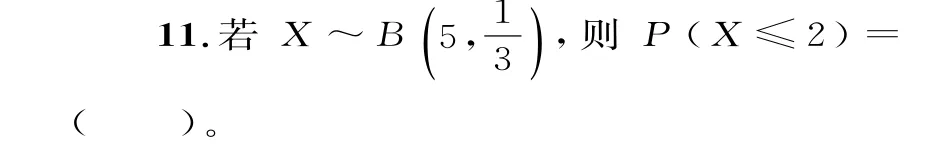
1 2.口袋中有编号分别为1,2,3的3个大小和形状相同的小球,从中任取2个,则取出的球的最大编号X的期望为( )。

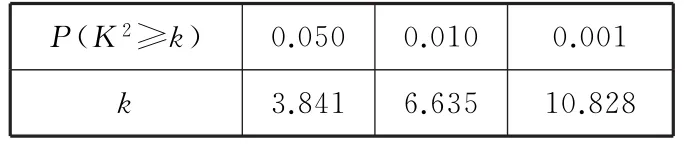
表3

参照附表,得到的正确结论是( )。

A.在犯错误的概率不超过0.1%的前提下,认为“爱好该项运动与性别有关”

B.在犯错误的概率不超过0.1%的前提下,认为“爱好该项运动与性别无关”

C.有9 9%以上的把握认为“爱好该项运动与性别有关”

D.有9 9%以上的把握认为“爱好该项运动与性别无关”

1 8.在1,2,3,4,5这5个数字组成的没有重复数字的三位数中,各位数字之和为奇数的共有( )。

A.3 6个 B.2 4个

C.1 8个 D.6个

1 9.某篮球队有1 2名球员,按其所站位置可分为3名中锋,4名后卫,5名前锋。某一场比赛进行中,教练员拟派出1名中锋,2名后卫和2名前锋的标准阵容。现已知中锋甲与后卫乙不能同时上场,则不同的选派方法种数为( )。

A.1 8 0 B.1 5 0 C.1 2 0 D.1 0 8

2 0.随着人们生活水平的不断提高,汽车作为出行的代步工具越来越普及,这给人们带来了极大便利的同时也产生了一系列的问题,比如“停车难”。某小区物业结合小区情况,通过挖掘自身条件,新增7个停车位,并面向全体业主招租。现有1 0名业主,但有1 2辆汽车,其中有2名业主各有2辆汽车。本

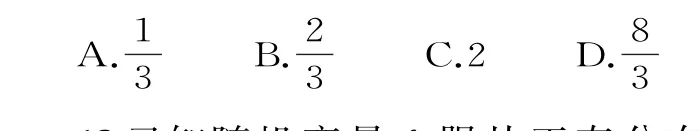
1 3.已知随机变量ξ服从正态分布N(2,σ2),若 P(ξ≤4)=0.8 4,则 P(ξ＜0)等于( )。

A.0.1 6 B.0.3 2 C.0.6 8 D.0.8 4

1 4.某商品销售量y(件)与销售价格x(元/件)负相关,则其回归方程可能是( )。

A.^y=-1 0x+2 0 0 B.^y=1 0x+2 0 0

C.^y=-1 0x-2 0 0 D.^y=1 0x-2 0 0

1 5.某产品的广告费用x与销售额y的统计数据如表1:

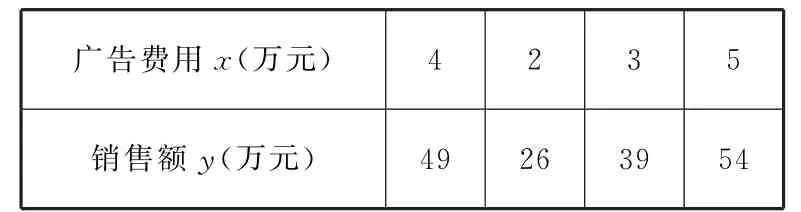
表1

根据上表可得回归方程^y=^b x+^a中的^b为9.4,据此模型预报广告费用为6万元时销售额为( )。

A.6 3.6万元 B.6 5.5万元

C.6 7.7万元 D.7 2.0万元

1 6.在一个2×2列联表中,由其数据计算得K2的观测值k=7.0 9 7,则这两个变量间有关系的可能性为( )。

A.9 9% B.9 9.5%

C.9 9.9% D.无法确定

1 7.通过随机询问1 1 0名性别不同的大学生是否爱好某项运动,得到如下的列联表:附表(表3):着“公平、公开、公正”的原则,物业决定采用“抽签摇号”的方式进行确认,并提出同一业主最多只能1辆车中签,且要求一车一号,则不同的结果有( )种。

表2

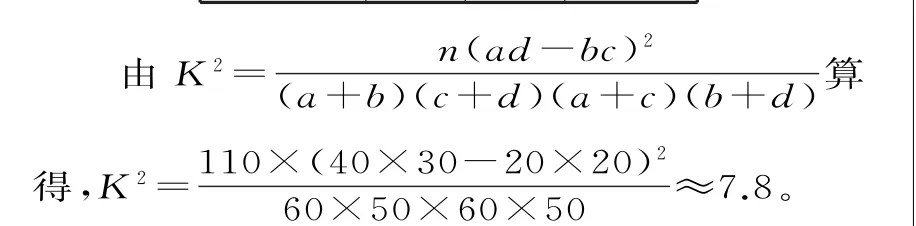
A.2 2 4 B.3 3 6 C.3 4 4 D.3 3 4

2 1.2位学生一起去一家单位应聘,面试前,单位负责人对他们说:“我们要从面试的人中招聘3人,若每人被招聘的概率相同,则你们俩同时被招聘进来的概率是1。”根据这7位负责人的话,可以推断出参加面试的人数为( )。

A.5 B.7 C.8 D.92 2.已知的展开式中,各项系数的和是各项的二项式系数之和的6 4倍,则实数n的值为( )。

A.4 B.5 C.6 D.7 2 3.若

的展开式中x3的系数为,则常数a的值为( )。

A.1 B.3 C.4 D.9的展开式中,x3项的系数为( )。

A.2 0 B.3 0 C.3 5 D.4 0

2 5的展开式中系数最大的项为( )。

2 6.在(1-x)3(1+x)8的展开式中,含x2项的系数是n,若(8-n x)n=a0+a1x+a2x2+…+anxn,则a0+a1+a2+…+an=( )。

A.0 B.1 C.-1 D.1 57个供只所区选涂涂2域 择一颜7.,,种色如现要颜不图有求色同14每,,种一相则所颜个邻不示色区区同的可域域的5涂色方法数为( )。 图1

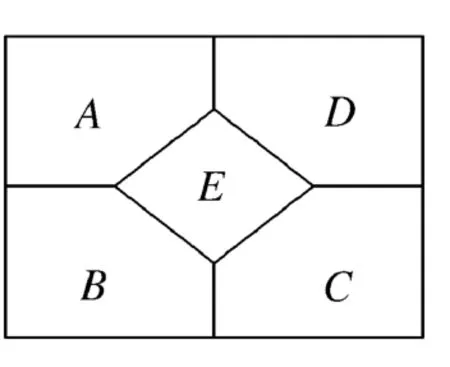
A.2 4 B.4 8 C.7 2 D.9 6

2 8.将标号为1,2,3,4的4个篮球分给3位小朋友,每位小朋友至少分到1个篮球,且标号1,2的2个篮球不能分给同一个小朋友,则不同的分法数为( )。

A.1 5 B.3 0 C.2 0 D.4 2

2 9.某校从8名教师中选派4名教师去4个边远地区支教(每地1名教师),其中甲和乙不能都去,甲和丙只能都去或都不去,则不同的选派方案有( )。

A.9 0 0种 B.6 0 0种

C.3 0 0种 D.1 5 0种

3 0.设a∈Z,且0≤a＜1 3,若5 12016+a能被1 3整除,则a=( )。

A.0 B.1 C.1 1 D.1 2

3 1.甲、乙两人单独对同一目标各射击一次,命中率分别为0.6和0.5,现已知目标被击中,则它是被甲击中的概率为( )。

A.0.4 5 B.0.6 C.0.6 5 D.0.7 5

3 2.甲打靶时每打1 0次,可中靶8次;乙每打1 0次,可中靶7次。若2人同时射击一个目标,则它们都中靶的概率是( )。

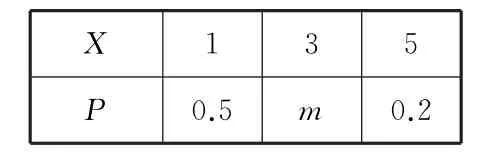
表4

则其方差D(X)=( )。

A.2.4 4 B.0.6 C.2.4 D.1

3 6.已知变量x与y之间的回归直线方程为^y=-3+2x,若=1 7,则的值等于( )。

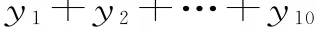
A.3 B.4 C.0.4 D.4 0

3 3.已知随机变量X服从正态分布N,且P(X＜5)=0.8,则P(1＜X＜3)=( )。

A.0.6 B.0.4 C.0.3 D.0.2

3 4.已知X+Y=8,若X～B(1 0,0.6),则E(Y)和D(Y)分别是( )。

A.6和2.4 B.2和2.4

C.2和5.6 D.6和5.6

3 5.已知离散型随机变量X的概率分布列为:

3 7.研究人员在研究人体脂肪含量和年龄关系时获得了一组样本数据,并制作成如图2所示的人体脂肪含量与年龄关系的散点图。根据该图,判断下列结论中正确的是( )。

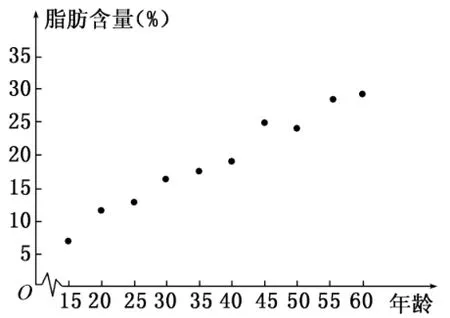
图2

A.人体脂肪含量与年龄正相关,且脂肪含量的中位数等于2 0%

B.人体脂肪含量与年龄正相关,且脂肪含量的中位数小于2 0%

C.人体脂肪含量与年龄负相关,且脂肪含量的中位数等于2 0%

D.人体脂肪含量与年龄负相关,且脂肪含量的中位数小于2 0%

3 8.下列说法错误的是( )。

A.自变量取值一定时,因变量的取值带有一定随机性的两个变量之间的关系称为相关关系

B.在线性回归分析中,相关系数r的值越大,变量间的相关性越强

C.在残差图中,残差点分布的带状区域的宽度越狭窄,其模型拟合的精度越高

D.在回归分析中,R2为0.9 8的模型比R2为0.8 0的模型拟合的效果好

3 9.在两个学习进度相当的班级实行某种教学措施的实验,测试结果见表5,则在犯错误的概率不超过0.0 0 5的前提下推断实验效果与教学措施( )。

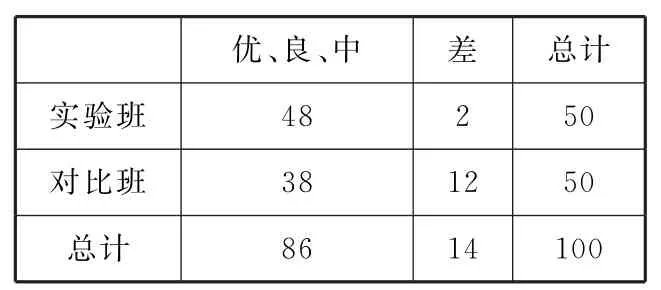
表5

A.有关 B.无关

C.关系不明确 D.以上都不正确

4 0.甲、乙、丙3人站到共有7级的台阶上,每级台阶最多站2人,同一级台阶上的人不区分站的位置,则不同的站法数是( )。

A.1 2 6 B.3 3 6 C.7 7 D.2 5 2

二、填空题

4 1.从集合{0,1,2,3,4,5,6}中任取2个互不相等的数a,b组成复数a+bi,其中虚数有____个。

4 2.若正整数n满足C31n8+6=C41n8-2,则n的值为____。

4 3.8种不同的菜种,任选4种种在不同土质的4块地上,有____种不同的种法。(用数字作答)

4 4.某餐厅供应饭菜,每位顾客可以在餐厅提供的菜肴中任选2荤2素共4种不同的品种。现在餐厅准备了5种不同的荤菜,若要保证每位顾客有2 0 0种以上不同的选择,则餐厅至少还需准备____种不同的素菜。(结果用数值表示)

4 5.已知(a+b)n的二项展开式中只有第5项的二项式系数最大,则n等于____。

1n

4 6.若(x +x)的展开式的二项式系数之和为6 4,则展开式的常数项为____。

4 7.若随机变量X服从两点分布,且P(X=0)=0.8,P(X=1)=0.2,令Y=3X-2,则P(Y=-2)=____。

4 8.某一随机变量ξ的概率分布列如表6,且m+2n=1.2,则m-n的值为____。2

表6

4 9.盒中装有1 0只乒乓球,其中6只新球,4只旧球,不放回地依次取出2只球,在第一次摸出新球的条件下,第二次也取到新球的概率为____。

5 0.某篮球队员在比赛中每次罚球的命中率相同,且在两次罚球中至多命中一次的概率为1 6,则该队员每次罚球的命中率为____。2 5

5 1.某同学参加一次考试,已知4道题中答对3道则为及格,若他的解题正确率为0.4,则他能及格的概率为____。

5 2.设1 50 0 0件产品中有10 0 0件次品,从中抽取1 5 0件进行检查,由于产品数量较大,每次检查的次品率看成不变,则查得次品数的数学期望为 。

5 3.随机变量ξ的分布列如下(表7):

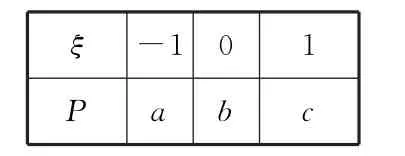
表7

其中a,b,c成等差数列,若则D(ξ)=。

5 4.如果ξ～N(μ,σ2),且 P(ξ＞3)=P(ξ＜1)成立,那么μ=。

5 5.如果散点图的所有点都在一条直线上,则残差均为,残差平方和为,相关指数为 。

5 6.对具有线性相关关系的变量x和y,由测得的一组数据求得回归直线的斜率为6.5,且恒过(2,3)点,则这条回归直线的方程为 。

5 7.图3是x和y的一组样本数据的散点图,去掉一组数据

后,剩下的4组数据的相关指数最大。

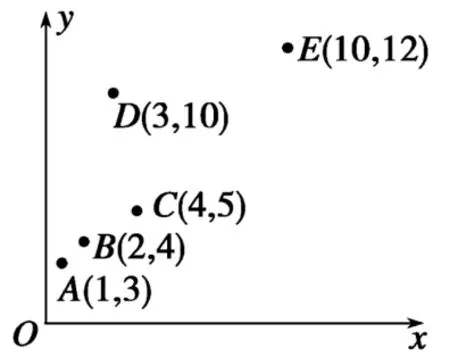
图3

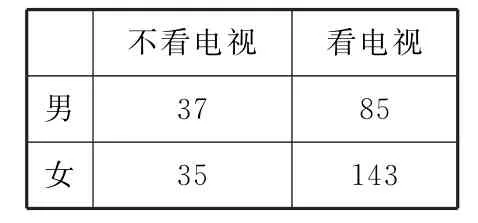
表8

5 8.根据表8计算:则K2的观测值k≈ 。(保留3位小数)5 9.为了解高中生作文成绩与课外阅读量之间的关系,某研究机构随机抽取了6 0名高中生,通过问卷调查,得到以下数据(表9):

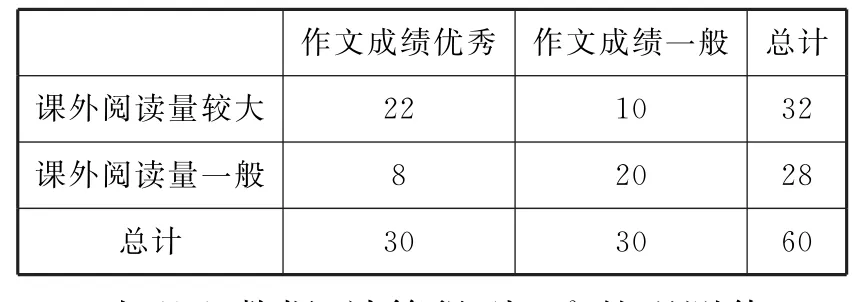
表9

由以上数据,计算得到K2的观测值k≈9.6 4 3,根据临界值表,有 的把握认为课外阅读量大与作文成绩优秀有关。

三、解答题

6 0.用0,1,2,3,4,5这6个数字:

(1)可以组成多少个没有重复数字的三位数?

(2)可以组成多少个允许重复的三位数?

(3)可以组成多少个数字不允许重复的三位奇数?

(4)可以组成多少个数字不允许重复且小于10 0 0的自然数?

(5)可以组成多少个大于30 0 0,且小于54 2 1的不重复的四位数?

6 1.有4个不同的球,4个不同的盒子,把球全部放入盒内,问:

(1)共有多少种放法?

(2)恰有1个盒不放球,有多少种放法?

(3)恰有1个盒内放2个球,有多少种放法?

(4)恰有2个盒内不放球,有多少种放法?

6 2.已知(1-2x)7=a0+a1x+a2x2+…+a7x7,求下列各式的值:

(1)a1+a2+…+a7;

(2)a1+a3+a5+a7;

(3)|a0|+|a1|+|a2|+…+|a7|。

6 3.某大学志愿者协会有6名男同学,4名女同学。在这1 0名同学中,3名同学来自数学学院,其余7名同学来自物理、化学等其他互不相同的7个学院。现从这1 0名同学中随机选取3名同学,到希望小学进行支教活动(每位同学被选到的可能性相同)。

(1)求选出的3名同学是来自互不相同学院的概率;

(2)设X为选出的3名同学中女同学的人数,求随机变量X的分布列及其期望值。

6 4.某学校举行知识竞赛,第一轮选拔共设有1,2,3三个问题,每位参赛者按问题1,2,3的顺序作答,竞赛规则如下:

①每位参赛者计分器的初始分均为1 0分,答对问题1,2,3分别加1分,2分,3分,答错任一题减2分。

②每回答一题,积分器显示累计分数,当累计分数小于8分时,答题结束,淘汰出局;当累计分数大于或等于1 2分时,答题结束,进入下一轮;当答完三题,累计分数仍不足1 2分时,答题结束,淘汰出局。

已知甲同学回答1,2,3三个问题正确的概率依次为,且各题回答正确与否相互之间没有影响。

(1)求甲同学能进入下一轮的概率;

(2)用X表示甲同学本轮答题结束时累计分数,求X的分布列和数学期望。

6 5.为了解今年某校高三毕业班准备报考飞行员学生的体重情况,将所得的数据整理后,画出了频率分布直方图(如图4),已知图中从左到右的前3个小组的频率之比为1∶2∶3,其中第2小组的频数为1 2。

(1)求该校报考飞行员的总人数;

(2)以这所学校的样本数据来估计全省的总体数据,若从全省报考飞行员的学生中(人数很多)任选3人,设X表示体重超过6 0k g的学生人数,求X的分布列和数学期望。

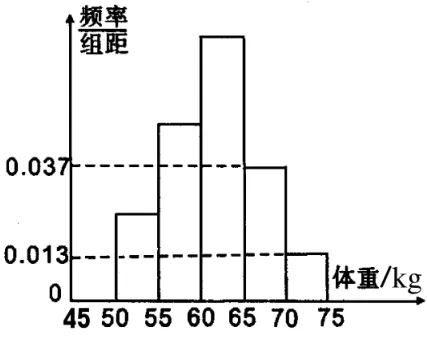
图4

6 6.有甲、乙两个班级进行数学考试,按照大于等于8 5分为优秀,8 5分以下为非优秀统计成绩后,得到如下的列联表(表1 0):

表1 0

已知在全部1 0 5人中抽到随机抽取1人为优秀的概率为

(1)请完成上面的列联表。

(2)根据列联表的数据,若按9 5%的可靠性要求,能否认为“成绩与班级有关系”?

(3)若按下面的方法从甲班优秀的学生抽取一人:把甲班优秀的1 0名学生从2到1 1进行编号,先后两次抛掷一枚均匀的骰子,出现的点数之和为被抽取人的序号。试求抽到6或1 0号的概率。

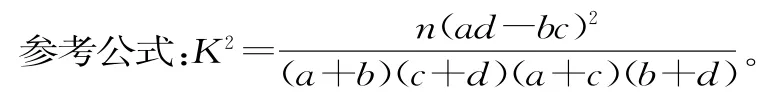
参考数据:

表1 1

6 7.生产工艺工程中产品的尺寸偏差X(mm)～N(0,22),如果产品的尺寸与现实的尺寸偏差的绝对值不超过4mm的为合格品,求生产5件产品的合格率不小于8 0%的概率。(精确到0.0 0 1)

6 8.某种产品的广告费支出x(单位:百万元)与销售额y(单位:百万元)之间有如下对应数据:

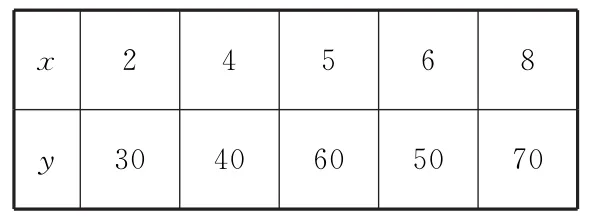
表1 2

(1)画出散点图;

(2)求线性回归直线方程;

(3)试预测广告费支出为1 0百万元时销售额多大。

6 9.一名同学连续抛掷同一颗均匀的骰子,令第i次得到的点数为ai,若存在正整数k,使a1+a2+…+ak=6,则称k为该同学的幸福数字。

(1)求该同学的幸福数字为2的概率。

(2)若k=1,则该同学的得分为5分;若k=2,则该同学的得分为3分;若k=3,则该同学的得分为1分;若抛掷三次还没找到该同学的幸福数字则记0分,求得分X的分布列和数学期望。