离散型随机变量的分布列、期望和方差高考链接
■山东枣庄二中 杨文金
一、高考考情
离散型随机变量的均值与方差是高考的热点,主要考查同学们对取有限个值的离散型随机变量的均值、方差的理解,要求同学们能计算简单离散型随机变量的均值、方差,并能解决一些实际问题。若单独考查,一般以客观题形式出现,主要考查利用公式进行计算,难度不大。若以解答题形式出现,一般不单独考查,常见命题方式有两种:一是与概率、分布列计算结合在一起进行考查,二是与统计结合在一起进行考查,难度中等。
二、要点整合
1.高考对离散型随机变量的均值与方差的考查主要有以下三个命题角度:
(1)已知离散型随机变量符合条件,求其均值与方差;
(2)已知离散型随机变量的均值与方差,求参数值;
(3)已知离散型随机变量满足两种方案,试作出判断。
2.求离散型随机变量均值、方差的基本方法:
(1)已知随机变量的分布列求它的均值、方差和标准差,可直接按定义(公式)求解;
(2)已知随机变量ξ的均值、方差,求ξ的线性函数η=aξ+b的均值、方差和标准差,可直接用ξ的均值、方差的性质求解;
(3)如能分析所给随机变量服从常用的分布(如两点分布、二项分布等),可直接利用它们的均值、方差公式求解。
3.解答题中对期望与方差的考查常与分布列结合在一起进行考查,求解此类问题要先根据随机变量的定义,确定随机变量可以取哪些值,然后根据随机变量取这些值的意义求出取这些值的概率,列出分布列,根据均值与方差的公式计算,若随机变量服从二项分布,可直接利用公式E(X)=n p,D(X)=n p(1-p)求解。
4.均值与方差的实际应用。
对于均值与方差的实际应用,命题模式通常是已知离散型随机变量满足两种方案,试作出判断。求解这类问题要用到均值与方差。
(1)D(X)表示随机变量X对E(X)的平均偏离程度,D(X)越大表明平均偏离程度越大,说明X的取值越分散;反之,D(X)越小,X的取值越集中在E(X)附近,统计中常用来描述X的分散程度。
(2)随机变量的均值反映了随机变量取值的平均水平,方差反映了随机变量取值偏离于均值的程度,它们从整体和全局上刻画了随机变量,是生产实际中用于方案取舍的重要的理论依据,一般先比较均值,若均值相同,再用方差来决定。
三、考题选析
例1 (2 0 1 7年新课标Ⅲ卷理)某超市计划按月订购一种酸奶,每天进货量相同,进货成本每瓶4元,售价每瓶6元,未售出的酸奶降价处理,以每瓶2元的价格当天全部处理完。根据往年销售经验,每天需求量与当天最高气温(单位:℃)有关。如果最高气温不低于2 5,需求量为5 0 0瓶;如果最高气温位于区间[2 0,2 5),需求量为3 0 0瓶;如果最高气温低于2 0,需求量为2 0 0瓶。为了确定六月份的订购计划,统计了前三年六月份各天的最高气温数据,得下面的频数分布表(见表1):

表1
以最高气温位于各区间的频率代替最高气温位于该区间的概率。
(1)求六月份这种酸奶一天的需求量X(单位:瓶)的分布列;
(2)设六月份一天销售这种酸奶的利润为Y(单位:元),当六月份这种酸奶一天的进货量n(单位:瓶)为多少时,Y的数学期望达到最大值?
解:(1)由题意得,X可取2 0 0,3 0 0,5 0 0。

故X的分布列为:

表2
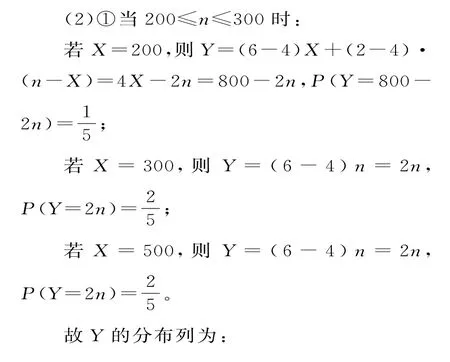
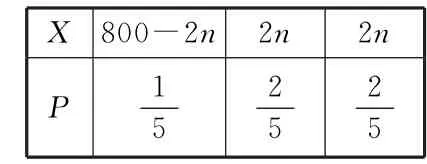
表3
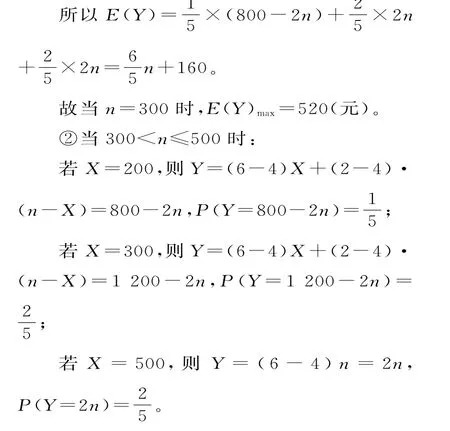
所以Y的分布列为:6 4 0=5 2 0(元)。

表4
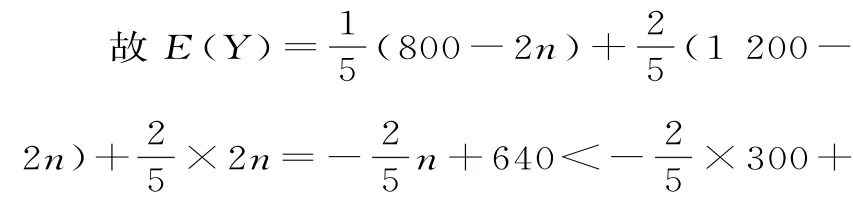
综上,当n为3 0 0瓶时,Y的数学期望达到最大值。
点评:本题把随机变量的分布列与统计及函数结合在一起进行考查,有一定的综合性,但难度不是太大,求解关键是读懂题意,所以同学们学习时要重视数学中的阅读理解问题。
例2(2 0 1 7年新课标Ⅰ卷理)为了监控某种零件的一条生产线的生产过程,检验员每天从该生产线上随机抽取1 6个零件,并测量其尺寸(单位:c m)。根据长期生产经验,可以认为这条生产线正常状态下生产的零件的尺寸服从正态分布N(μ,σ2)。
(1)假设生产状态正常,记X表示一天内抽取的1 6个零件中其尺寸在(μ-3σ,μ+3σ)之外的零件数,求P(X≥1)及X的数学期望。
(2)一天内抽检零件中,如果出现了尺寸在(μ-3σ,μ+3σ)之外的零件,就认为这条生产线在这一天的生产过程可能出现了异常情况,需对当天的生产过程进行检查。
(ⅰ)试说明上述监控生产过程方法的合理性;
(ⅱ)下面是检验员在一天内抽取的1 6个零件的尺寸:0.2 1 2,其中为抽取的第i个零件的尺寸,i=1,2,…,1 6。

表5


用样本平均数x 作为μ的估计值^μ,用样本标准差s作为σ的估计值^σ,利用估计值判断是否需对当天的生产过程进行检查。剔除)之外的数据,用剩下的数据估计μ和σ(精确到0.0 1)。
附:若随机变量Z服从正态分布N(μ,σ2),则P(μ-3σ<Z<μ+3σ)=0.9 9 74,0.9 9 7416≈0.9 5 92,0.0 0 8≈0.0 9。
分析:(1)根据题设条件知一个零件的尺寸在(μ-3σ,μ+3σ)之内的概率为0.9 9 74,则零件的尺寸在(μ-3σ,μ+3σ)之外的概率为0.0 0 26,而X~B(1 6,0.0 0 26),进而可以求出X的数学期望。(2)(i)判断监控生产过程的方法的合理性,重点是考虑一天内抽取的1 6个零件中,出现尺寸在(μ-3σ,μ+3σ)之外的零件的概率大还是小,若小即合理;(i i)根据题设条件算出μ的估计值和σ的估计值,剔除之外的 数据9.2 2,算出剩下数据的平均数,即为μ的估计值,剔除之 外的数 据 9.2 2,剩下数据的样本方差,即为σ的估计值。
解:(1)抽样的一个零件的尺寸在(μ-3σ,μ+3σ)之内的概率为0.9 9 74,从而零件的尺寸在 (μ-3σ,μ+3σ)之外的概率为0.0 0 26,故X~B(1 6,0.0 0 26),因此:
P(X≥1)=1-P(X=0)=1-0.9 9 7416=0.0 4 08。
X的数学期望为E X=1 6×0.0 0 26=0.0 4 16。
(2)(i)如果生产状态正常,一个零件尺寸 在 (μ-3σ,μ+3σ)之 外 的 概 率 只 有0.0 0 26,一天内抽取的1 6个零件中,出现尺寸在(μ-3σ,μ+3σ)之外的零件的概率只有0.0 4 08,发生的概率很小。因此一旦发生这种情况,就有理由认为这条生产线在这一天的生产过程可能出现了异常情况,需对当天的生产过程进行检查,可见上述监控生产过程的方法是合理的。
(i i)由¯x=9.9 7,s≈0.2 1 2,得μ的估计值为^μ=9.9 7,σ的估计值为^σ=0.2 1 2,由样本数据可以看出有一个零件的尺寸在(^μ-3^σ,^μ+3^σ)之外,因此需对当天的生产过程进行检查。
剔除(^σ-3^σ,^μ+3^σ)之外的 数据9.2 2,剩下数据的平均数为1 0.0 2,因此μ的估计值为1 0.0 2。15 9 1.1 3 4,剔 除)之 外 的 数 据9.2 2,剩下数据的样本方差为
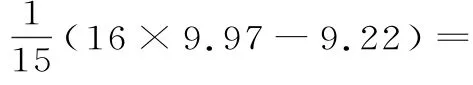
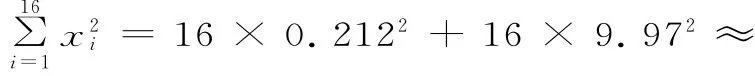

因此σ的估计值为 0.0 0 8≈0.0 9。
点评:数学期望是离散型随机变量中重要的数学概念,反映随机变量取值的平均水平。求解离散型随机变量的分布列、数学期望时,首先要分清事件的构成与性质,确定离散型随机变量的所有取值,然后根据概率类型选择公式,计算每个变量取每个值的概率,列出对应的分布列,最后求出数学期望。正态分布是一种重要的分布,之前考过一次,尤其是正态分布的3σ原则。

