随机变量及其分布考点突破

■山东省枣庄二中 罗桂花

一、高考定位

概率模型多考查独立重复试验、相互独立事件、互斥事件及对立事件等知识;而离散型随机变量的分布列及期望也是考试中的“热点”,并且多以解答题形式出现,常考查独立事件的概率,超几何分布和二项分布的期望等。

二、考点例析

考点1：相互独立事件的概率

例1 (2 0 1 6年高考北京卷)A、B、C三个班共有1 0 0名学生,为调查他们的体育锻炼情况,通过分层抽样获得了部分学生一周的锻炼时间,数据如表1:

表1

(1)试估计C班的学生人数。

(2)从A班和C班抽出的学生中,各随机选取一人,A班选出的学生记为甲,C班选出的学生记为乙,假设所有学生的锻炼时间相对独立,求一周中甲的锻炼时间比乙的锻炼时间长的概率。

(3)再从A、B、C三个班中各随机抽取一名学生,他们该周的锻炼时间分别是7,9,8.2 5(单位:小时),这3个新数据与表格中的数据构成的新样本的平均数记μ1,表格中数据的平均数记为μ0,试判断μ0和μ1的大小(结论不要求证明)。

分析：(1)由分层抽样的抽样比估算出C班的学生人数。

(2)根据题意列出“该周甲的锻炼时间比乙的锻炼时间长”的所有事件,由独立事件概率公式求值。

(3)根据平均数公式进行判断即可。

解：(1)由题意知,抽出的2 0名学生中,来自C班的学生有8名,根据分层抽样方法知,C班的学生人数估计为1 0 0×8=4 0。2 0

(2)设事件Ai为“甲是现有样本中A班的第i个人”,i=1,2,…,5。

事件Cj为“乙是现有样本中C班的第j个人”,j=1,2,…,8。

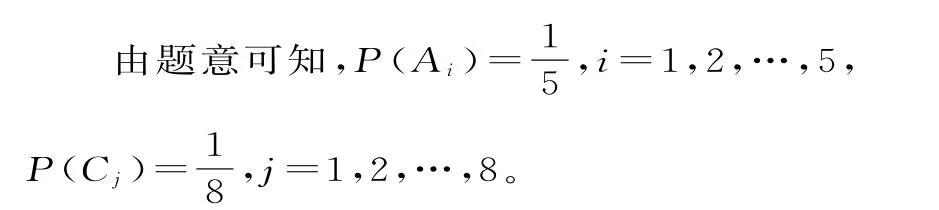
设事件E为“一周中甲的锻炼时间比乙的锻炼时间长”,由题意可知:

E=A1C1∪A1C2∪A2C1∪A2C2∪A2C3∪A3C1∪A3C2∪A3C3∪A4C1∪A4C2∪A4C3∪A5C1∪A5C2∪A5C3∪A5C4。

因此P(E)=P(A1C1)+P(A1C2)+P(A2C1)+P(A2C2)+P(A2C3)+P(A3C1)+P(A3C2)+P(A3C3)+P(A4C1)+P(A4C2)+P(A4C3)+P(A5C1)+P(A5C2)+P(A5C3)+P(A5C4)

(3)根据平均数计算公式即可知,μ1＜μ0。

点评:对于复杂事件的概率,要先分析事件的构成,理清各事件之间的关系,并依据互斥事件概率的和,或者相互独立事件概率的积的公式列出关系式。

考点2：独立重复试验的概率

例2 (2 0 1 6年临沂模拟卷)一家面包房根据以往某种面包的销售记录,绘制了日销售量的频率分布直方图,如图1所示。

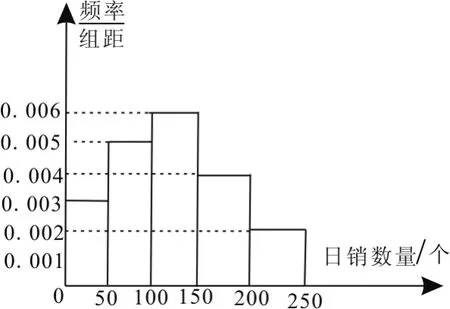
图1

将日销售量落入各组的频率视为概率,并假设每天的销售量相互独立。

(1)求在未来3天里,有连续2天的日销售量都不低于1 0 0个且另一天的日销售量低于5 0个的概率。

(2)用X表示在未来3天里日销售量不低于1 0 0个的天数,求随机变量X的分布列,期望E(X)及方差D(X)。

解析：(1)设A1表示事件“日销售量不低于1 0 0个”,A2表示事件“日销售量低于5 0个”,B表示事件“在未来连续3天里,有连续2天的日销售量都不低于1 0 0个且另一天的日销售量低于5 0个”,因此有:X的分布列为:

X 0 1 2 3 P 0.0 6 4 0.2 8 8 0.4 3 2 0.2 1 6

因为X～B(3,0.6),所以期望E(X)=3×0.6=1.8,方差D(X)=3×0.6×(1-0.6)=0.7 2。

点评:在解题时注意独立重复试验的基本特征:(1)在每次试验中,试验结果只有发生与不发生两种情况;(2)在每次试验中,事件发生的概率相同。

考点3：条件概率

例3 (2 0 1 6年高考新课标Ⅱ卷理科数学)某险种的基本保费为a(单位:元),继续购买该险种的投保人称为续保人,续保人的本年度的保费与其上年度的出险次数的关联如下:

上年度出险次数 0 1 2 3 4 ≥5保费 0.8 5a a 1.2 5a 1.5a 1.7 5a 2a

设该险种一续保人一年内出险次数与相应概率如下:

一年内出险次数 0 1 2 3 4 ≥5概率 0.3 0 0.1 5 0.2 0 0.2 0 0.1 0 0.0 5

(1)求一续保人本年度的保费高于基本保费的概率;

(2)若一续保人本年度的保费高于基本保费,求其保费比基本保费高出6 0%的概率;

(3)求续保人本年度的平均保费与基本保费的比值。

分析：(1)根据互斥事件的概率公式,可求一续保人本年度的保费高于基本保费的概率;(2)当且仅当一年内出险次数大于3,一续保人本年度的保费才高于基本保费6 0%,可由条件概率公式求解;(3)记续保人本年度的保费为X,求X的分布列及期望值。

解：(1)设A表示事件:“一续保人本年度的保费高于基本保费”,只有当一年内出险次数大于1,事件A才会发生,故P(A)=0.2 0+0.2 0+0.1 0+0.0 5=0.5 5。

(2)设B表示事件:“一续保人本年度的保费比基本保费高出6 0%”,则事件B只有当一年内出险次数大于3才会发生,故P(B)=0.1 0+0.0 5=0.1 5。

(3)记续保人本年度的保费为X,则X的分布列为:

X0.8 5a a 1.2 5a1.5a1.7 5a2a P 0.3 0 0.1 50.2 00.2 00.1 0 0.0 5

E(X)=0.8 5a×0.3 0+a×0.1 5+1.2 5a×0.2 0+1.5a×0.2 0+1.7 5a×0.1 0+2a×0.0 5=1.2 3a。

因此续保人本年度的平均保费与基本保费的比值为1.2 3。

点评:条件概率的求法:

(1)定义法,先求P(A)和P(A B),再由

(2)基本事件法,当基本事件满足有限性和等可能性时,可借助古典概率公式,先求事件A包含的基本事件数n(A),再在事件A发生的条件下求事件B包含的基本事件数

考点4：利用相互独立事件、互斥事件的概率求分布列

例4 乒乓球台面被网分隔成甲、乙两部分,如图2所示,甲部分有两个不相交的区域A、B,乙部分被划分为两个不相交的区域C、D。某次测试要求队员接到落点在甲上的球后向乙回球,并规定:回球落点在C上记3分,落点在D上记1分,其他情况记0分。对落点在A上的来球,队员小明回球的落点在C上的概率为,在D上的概率为;对落点在B上的来球,小明回球的落点在C上的概率为,在D上的概率为。假设共有两次来球且落在A、B上各一次,小明的两次回球互不影响。求:

(1)小明两次回球的落点中恰有一次的落点在乙上的概率;

(2)两次回球结束后,小明得分之和ξ的分布列与数学期望。

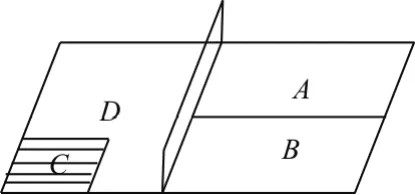
图2

解析：(1)记Ai为事件“小明对落点在A上回球的得分为i分”,i=0,1,3。

记Bi为事件“小明对落点在B上回球的得分为i分”,i=0,1,3。

记D为事件“小明两次回球的落点中恰有一次的落点在乙上”。

由题意知,D=A3B0+A1B0+A0B1+A0B3,由事件的独立性和互斥性可得:

P(D)=P(A3B0+A1B0+A0B1+A0B3)=P(A3B0)+P(A1B0)+P(A0B1)+P(A0B3)=P(A3)P(B0)+P(A1)P(B0)+P(A0)P(B1)+P(A0)P(B3)

所以小明两次回球的落点中恰有一次的落点在乙上的概率为

(2)由题意,随机变量ξ可能的取值为0,1,2,3,4,6。

由事件的独立性和互斥性,得:;

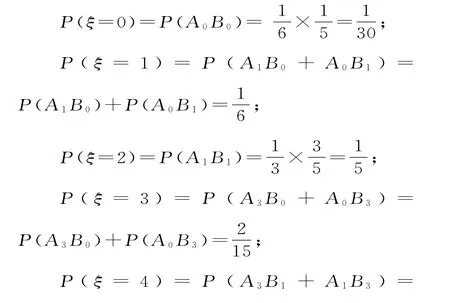
可得随机变量ξ的分布列为:

ξ 0 1 2 3 4 6 P 1 3 0 2 1 16 1 5 1 5 1 1 3 01 0

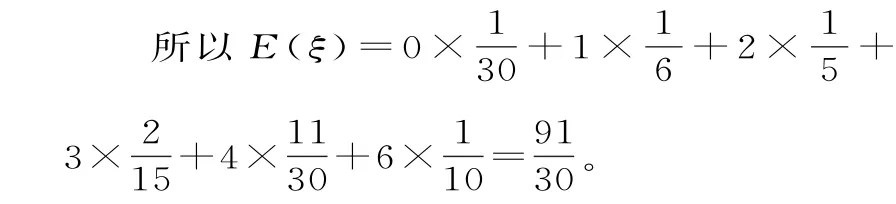
点评:解答这类问题要使用简洁、准确的数学语言,通过引进字母使得事件的描述简单而准确,或者用表格描述,使得问题描述有条理,从而答案不会有遗漏,也不会重复。

考点5：二项分布

例5 (2 0 1 5年高考湖北卷理科第2 0题)某厂用鲜牛奶在某台设备上生产A、B两种奶制品,生产1吨A产品需鲜牛奶2吨,使用设备1小时,获利10 0 0元;生产1吨B产品需鲜牛奶1.5吨,使用设备1.5小时,获利12 0 0元。要求每天B产品的产量不超过A产品产量的2倍,设备每天生产A、B两种产品时间之和不超过1 2小时。假定每天可获取的鲜牛奶数量W(单位:吨)是一个随机变量,其分布列为:

W 1 2 1 5 1 8 P 0.3 0.5 0.2

该厂每天根据获取的鲜牛奶数量安排生产,使其获利最大,因此每天的最大获利z(单位:元)是一个随机变量。

(1)求z的分布列和期望。

(2)若每天可获取的鲜牛奶数量相互独立,求3天中至少有1天的最大获利超过1 00 0 0元的概率。

解析：(1)设每天A、B两种产品的吨数分别为x、y,相应的获利为z元,则有:

目标函数为

当W=1 2时,(*)表示的平面区域如图3所示,三个顶点分别为A(0,0),B(2.4,4.8),C(6,0)。

图3

将z=10 0 0x+12 0 0y变形为当x=2.4,y=4.8时,直线在y轴上的截距最大,最大获利zmax=2.4×10 0 0+4.8×12 0 0=81 6 0。

当W=1 5时,(*)表示的平面区域如图4所示,三个顶点分别为A(0,0),B(3,6),C(7.5,0)。

将z=10 0 0x+12 0 0y在y轴上的截距最大。

图4

最大获利zmax=3×10 0 0+6×12 0 0=1 02 0 0。

当W=1 8时,(*)表示的平面区域如图5所示,四个顶点分别为A(0,0),B(3,6),C(6,4),D(9,0)。

将z=10 0 0x+12 0 0y在y轴上的截距最大。

图5

最大获利zmax=6×10 0 0+4×12 0 0=1 08 0 0。

z 81 6 0 1 02 0 0 1 08 0 0 P 0.3 0.5 0.2

故E(z)=81 6 0×0.3+1 02 0 0×0.5+1 08 0 0×0.2=97 0 8。

(2)由(1)知,一天最大获利超过1 00 0 0元的概率p1=P(z＞1 00 0 0)=0.5+0.2=

故最大获利z的分布列为:变形为0.7。

由二项分布知,3天中至少有1天最大获利超过1 00 0 0元的概率为:

p=1-(1-p1)3=1-0.33=0.9 7 3。

点评:二项分布是高中数学最重要的概率分布模型,是近年高考非常重要的一个考点。独立重复试验是相互独立事件的特例,就像对立事件是互斥事件的特例一样。

考点6：超几何分布

例6 (2 0 1 6年合肥市模拟卷)为推动乒乓球运动的发展,某乒乓球比赛允许不同协会的运动员组队参加。现有来自甲协会的运动员3名,其中种子选手2名;乙协会的运动员5名,其中种子选手3名。从这8名运动员中随机选择4人参加比赛。

(1)设A为事件“选出的4人中恰有2名种子选手,且这2名种子选手来自同一个协会”,求事件A发生的概率。

(2)设X为选出的4人中种子选手的人数,求随机变量X的分布列和数学期望。

解析：(1)由题意可知P(A)=

(2)随机变量X所有可能的取值为1,2,3,4。变量X的分布列为:

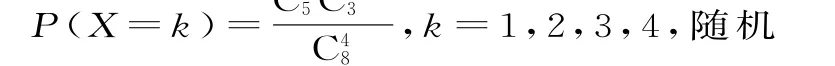
X 123 4 P 11 1 4 37 3 7 1 4

点评:抽取的4人中,可能是种子选手或一般运动员,并且只能是这两种情况之一,符合超几何概型的特征,故可利用超几何分布求其值。

考点7：正态分布

例7 (2 0 1 4年高考新课标全国Ⅰ卷)从某企业生产的某种产品中抽取 5 0 0件,测 量这些产品的一项质量指标值,由 测量结果得如图6所示的频率分布直方图。

图6

(1)求这5 0 0件产品质量指标值的样本平均数x和样本方差s2(同一组中的数据用该组区间的中点值作代表)。

(2)由直方图可以认为,这种产品的质量指标值Z服从正态分布N(μ,σ2),其中μ近似为样本平均数x,σ2近似为样本方差s2。

①利用该正态分布,求P(1 8 7.8＜Z＜2 1 2.2);

②某用户从该企业购买了1 0 0件这种产品,记X表示这1 0 0件产品中质量指标值位于区间(1 8 7.8,2 1 2.2)的产品件数,利用①的结果,求E(X)。

解析：(1)抽取产品的质量指标值的样本平均数x和样本方差s2分别为:

x=1 7 0×0.0 2+1 8 0×0.0 9+1 9 0×0.2 2+2 0 0×0.3 3+2 1 0×0.2 4+2 2 0×0.0 8+2 3 0×0.0 2=2 0 0;

s2=(-3 0)2×0.0 2+(-2 0)2×0.0 9+(-1 0)2×0.2 2+0×0.3 3+1 02×0.2 4+2 02×0.0 8+3 02×0.0 2=1 5 0。

(2)①由(1)知,Z～N(2 0 0,1 5 0),从而P(1 8 7.8＜Z＜2 1 2.2)=P(2 0 0-1 2.2＜Z＜2 0 0+1 2.2)=0.6 8 26。

②由①知,一件产品的质量指标值位于区间(1 8 7.8,2 1 2.2)的概率为0.6 8 26,依题意知X～B(1 0 0,0.6 8 26),所以E(X)=1 0 0×0.6 8 26=6 8.2 6。k4-k