离散型随机变量及其分布列高考热点透视

■河南省许昌市许昌高级中学 胡银伟

与实际生活密切相关的离散型随机变量的分布列、期望与方差问题,不但考查同学们的理解能力与数学计算能力,而且能够不断创新问题情境,突出考查同学们运用概率、期望与方差解决实际问题的能力,因此是高考的热点。从近几年高考命题情况来看,离散型随机变量及其分布列高考热点主要有以下两类。

热点一：对离散型随机变量分布列及期望的考查

例1 (2 0 1 7年全国Ⅲ卷)某超市计划按月订购一种酸奶,每天进货量相同,进货成本每瓶4元,售价每瓶6元,未售出的酸奶降价处理,以每瓶2元的价格当天全部处理完。根据往年销售经验,每天需求量与当天最高气温(单位:℃)有关。如果最高气温不低于2 5,需求量为5 0 0瓶;如果最高气温位于区间[2 0,2 5),需求量为3 0 0瓶;如果最高气温低于2 0,需求量为2 0 0瓶。为了确定六月份的订购计划,统计了前三年六月份各天的最高气温数据,得下面的频数分布表:

?

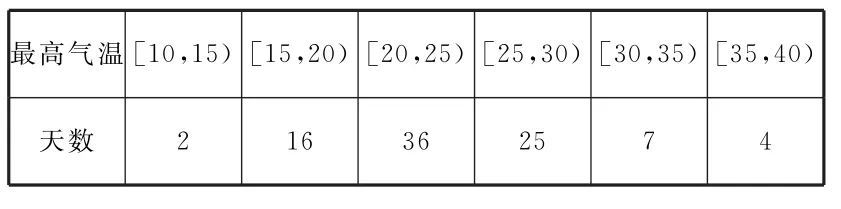
以最高气温位于各区间的频率代替最高气温位于该区间的概率。

(1)求六月份这种酸奶一天的需求量X(单位:瓶)的分布列;

(2)设六月份一天销售这种酸奶的利润为Y(单位:元),当六月份这种酸奶一天的进货量n(单位:瓶)为多少时,Y的期望达到最大值?

解析：(1)由题意知,X所有的可能取值

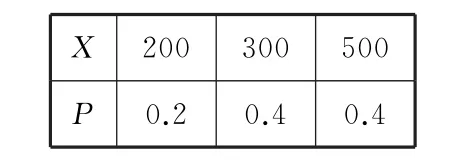
X2 0 0 3 0 0 5 0 0 P0.20.40.4

(2)由题意知,这种酸奶一天的需求量至多为5 0 0,至少为2 0 0,因此只需考虑2 0 0≤n≤5 0 0。

当3 0 0≤n≤5 0 0时:若最高气温不低于2 5,则Y=6n-4n=2n;

若最高气温位于区间[2 0,2 5),则Y=6×3 0 0+2(n-3 0 0)-4n=12 0 0-2n;

若最高气温低于2 0,则Y=6×2 0 0+2(n-2 0 0)-4n=8 0 0-2n。

此时,E(Y)=2n×0.4+(12 0 0-2n)×0.4+(8 0 0-2n)×0.2=6 4 0-0.4n。

当2 0 0≤n＜3 0 0时:若最高气温不低于2 0,则Y=6n-4n=2n;

若最高气温低于2 0,则Y=6×2 0 0+2(n-2 0 0)-4n=8 0 0-2n;

此时,E(Y)=2n×(0.4+0.4)+(8 0 0-2n)×0.2=1 6 0+1.2n。

所以当n=3 0 0时,Y的期望达到最大值,最大值为5 2 0元。

点评:求随机变量的数学期望和方差的关键是正确求出随机变量的分布列,而求随机变量及其分布列的一般步骤为:(1)明确随机变量的所有可能取值以及取每个取值所表示的意义;(2)利用排列组合知识或互斥事件、独立事件的概率公式求出随机变量取每个可能值的概率;(3)按规范形式写出随机变量的分布列,并用分布列的性质验证。

练习1：(2 0 1 7年天津卷)从甲地到乙地要经过3个十字路口,设各路口信号灯工作相互独立,且在各路口遇到红灯的概率分别为

(1)记X表示一辆车从甲地到乙地遇到红灯的个数,求随机变量X的分布列和数学期望;

(2)若有2辆车独立地从甲地到乙地,求这2辆车共遇到1个红灯的概率。

解析：(1)随机变量X的所有可能取值为0,1,2,3。

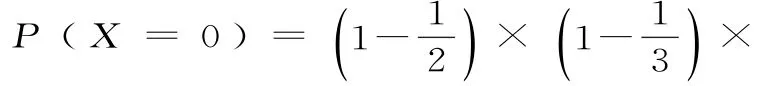
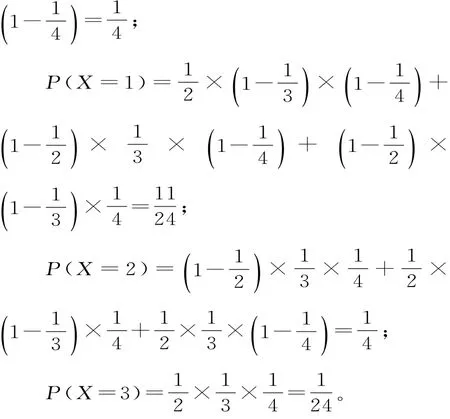
所以随机变量X的分布列为:

?

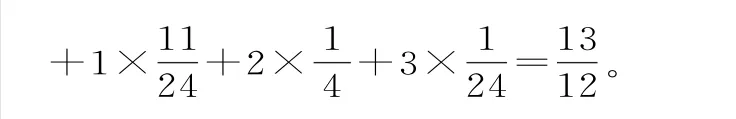
(2)设Y表示第一辆车遇到红灯的个数,Z表示第二辆车遇到红灯的个数,则所求事件的概率为:

P(Y+Z=1)=P(Y=0,Z=1)+P(Y=1,Z=0)=P(Y=0)P(Z=1)+所以这2辆车共遇到1个红灯的概率为

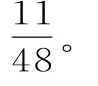
练习2：(2 0 1 7年山东卷)在心理学研究中,常采用对比试验的方法评价不同心理暗示对人的影响,具体方法如下:将参加试验的志愿者随机分成两组,一组接受甲种心理暗示,另一组接受乙种心理暗示,通过对比这两组志愿者接受心理暗示后的结果来评价两种心理暗示的作用。现有6名男志愿者A1,A2,A3,A4,A5,A6和4名女志愿者B1,B2,B3,B4,从中随机抽取5人接受甲种心理暗示,另5人接受乙种心理暗示。

(1)求接受甲种心理暗示的志愿者中包含A1但不包含B1的概率;

(2)用X表示接受乙种心理暗示的女志愿者人数,求X的分布列与数学期望E(X)。

解析：(1)记“接受甲种心理暗示的志愿者中包含A1但不包含B1”为事件为M,则

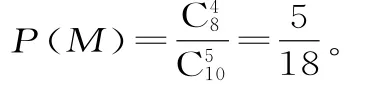
(2)由题意知X可取的值为:0,1,2,3,4,则:

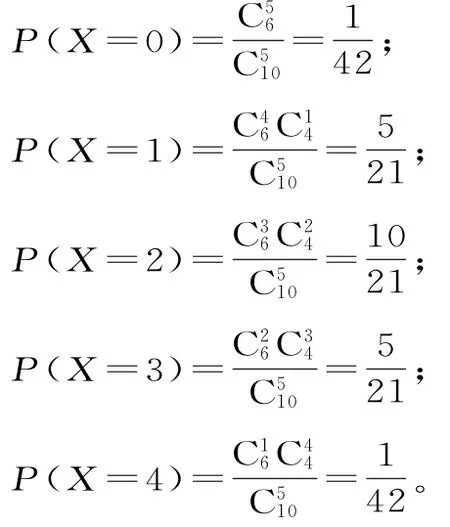
因此,X的分布列为:

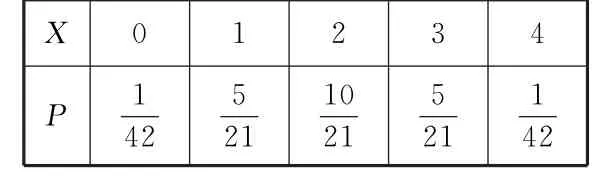
X 0 1 2 3 4 P1 4 2 5 51 2 1 1 0 2 12 14 2

热点二：对离散型随机变量期望与方差应用的考查

例2 为回馈顾客,某商场拟通过摸球兑奖的方式对10 0 0位顾客进行奖励,奖励规定:每位顾客从一个装有4个标有面值的球的袋中一次性随机摸出2个球,球上所标的面值之和为该顾客所获的奖励额。

(1)若袋中所装的4个球中有1个所标的面值为5 0元,其余3个均为1 0元,求:

①顾客所获的奖励额为6 0元的概率;

②顾客所获的奖励额的分布列及数学期望。

(2)商场对奖励总额的预算是6 00 0 0元,并规定袋中的4个球只能由标有面值1 0元和5 0元的两种球组成,或标有面值2 0元和4 0元的两种球组成。为了使顾客得到的奖励总额尽可能符合商场的预算且每位顾客所获的奖励额相对均衡,请对袋中的4个球的面值给出一个合适的设计,并说明理由。

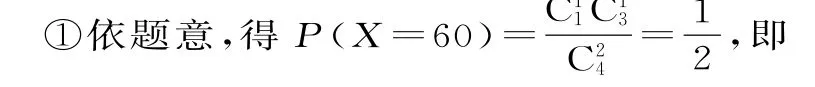
解析：(1)设顾客所获的奖励额为X。顾客所获的奖励额为6 0元的概率为。

②依题意,得X的所有可能取值为2 0,故X的分布列为:

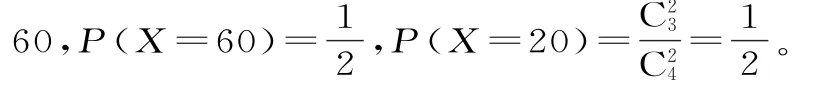
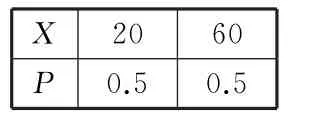
X 2 0 6 0 P0.50.5

所以顾客所获的奖励额的期望为E(X)=2 0×0.5+6 0×0.5=4 0(元)。

(2)根据商场的预算,每个顾客的平均奖励额为6 0元,所以先寻找期望为6 0元的可能方案。

对于面值由1 0元和5 0元组成的情况,假设选择(1 0,1 0,1 0,5 0)的方案,因为6 0元是面值之和的最大值,所以期望不可能为6 0元;假设选择(5 0,5 0,5 0,1 0)的方案,因为6 0元是面值之和的最小值,所以期望也不可能为6 0元,因此可能的方案是(1 0,1 0,5 0,5 0),记为方案1。

对于面值由2 0元和4 0元组成的情况,同理可排除(2 0,2 0,2 0,4 0)和(4 0,4 0,4 0,2 0)的方案,所以可能的方案是(2 0,2 0,4 0,4 0),记为方案2。

以下是对两个方案的分析:

对于方案1,即(1 0,1 0,5 0,5 0),设顾客所获的奖励额为X1,则X1的分布列为:

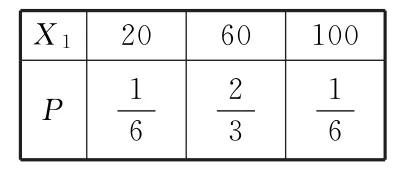
X12 0 6 0 1 0 0 P1 6 23 16

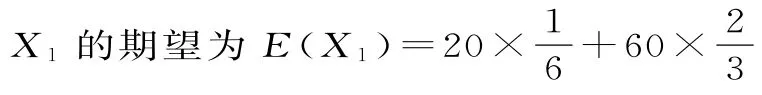
对于方案2,即(2 0,2 0,4 0,4 0),设顾客所获的奖励额为,则的分布列为:

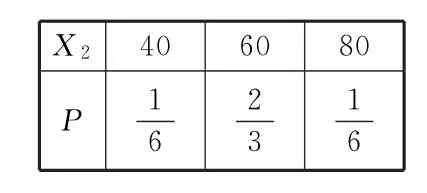
X24 0 6 0 8 0 P1 6 23 16

由于两种方案的奖励额的期望都符合要求,但方案2奖励额的方差比方案1的小,所以最优方案为方案2。

点评:解决概率的实际应用问题,要先根据题意确定概率模型,选择概率公式;对于离散型随机变量的分布列,要注意利用分布列的性质进行检验,特殊分布列的期望的计算可以直接利用公式,以简化计算过程。

期望能够反映随机变量取值的“平均水平”,因此,当期望不同时,两个随机变量取值的水平可见分晓,由此可对实际问题作出决策判断;在实际问题中,若两个随机变量ξ1,ξ2,有E(ξ1)=E(ξ2)或E(ξ1)与E(ξ2)较为接近时,就需要用D(ξ1)与D(ξ2)来比较两个随机变量的稳定程度。一般将期望最大(或最小)的方案作为最优方案,若各方案的期望相同,则选择方差最小(或最大)的方案作为最优方案。

练习3:现有两种投资方案,一年后投资盈亏的情况如下表:

投资股市:

投资结果 获利4 0% 不赔不赚 亏损2 0%概率 1 2 18 38

购买基金:

投资结果 获利2 0% 不赔不赚 亏损1 0%概率 p 1 3 q

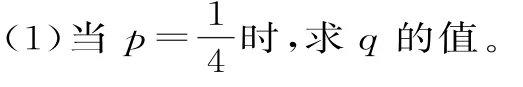
(2)已知甲乙两人分别选择了“投资股市”和“购买基金”进行投资,如果一年后他们中至少有一人获利的概率大于,求p的取值范围。

(3)丙要将家中闲置的1 0万元钱进行投资,决定在“投资股市”和“购买基金”这两种方案中选择一种,已知,那么丙选择哪种投资方案,才能使得一年后投资收益的数学期望较大?结合结果并说明理由。

解析：(1)因为“购买基金”后,投资结果只有“获利”“不赔不赚”“亏损”三种,且三种投资结果相互独立,所

又因为p=,所以q=。

(2)记事件A为“甲投资股市且盈利”,事件B为“乙购买基金且盈利”,事件C为“一年后甲乙两人中至少有一人投资获利”,则,且A,B相互独立。

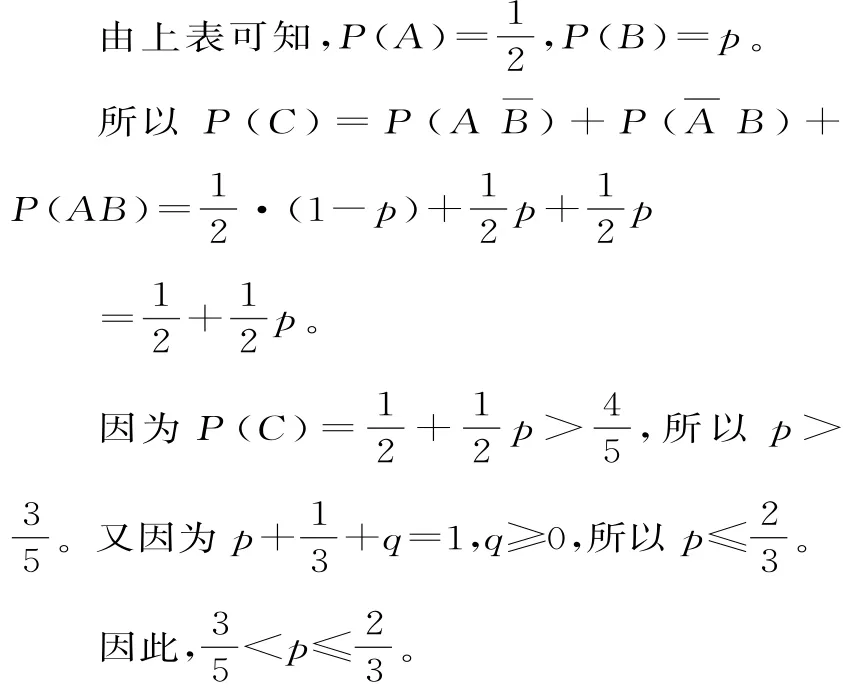
(3)假设丙选择“投资股市”方案进行投资,且记X为丙投资股市的获利金额(单位:万元),所以随机变量X的分布列为:

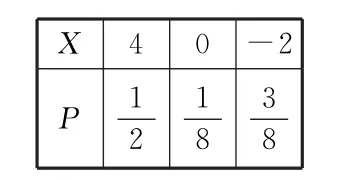
X40-2 P1 2 18 38

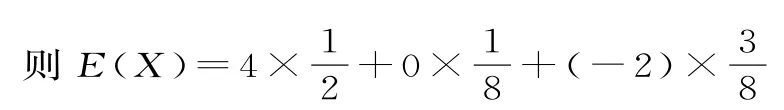
假设丙选择“购买基金”方案进行投资,且记Y为丙购买基金的获利金额(单位:万元),所以随机变量Y的分布列为:

Y20-1 P1 2 13 16

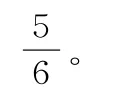
因为E(X)＞E(Y),所以丙选择“投资股市”才能使得一年后的投资收益的数学期望较大。