高考概率统计题命题探究

■山东枣庄二中 张运虎

研究近年来高考试卷,不难发现概率统计题也融入新课标的教育理念,多角度、多视点地考查学生的数学素养,使学生的自主性和个性得以发挥。体现数学与社会、人与自然的和谐统一。许多试题体现了时代气息,有创新特色。下面结合2 0 1 6年高考题谈谈高考概率统计题的命题特色。

一、关注学生的生活实际

这类题关注学生生活,试题中有大量生活背景,充分体现了“从生活走向数学,从数学走向生活”,符合新课标“学习资源和实践机会无所不在,无时不有”的理念。

例1(2 0 1 6年高考山东理数)某高校调查了2 0 0名学生每周的自习时间(单位:小时),制成了如图1所示的频率分布直方图,其中自习时间的范围是[1 7.5,3 0],样本数据分组为[1 7.5,2 0),[2 0,2 2.5),[2 2.5,2 5),[2 5,2 7.5),[2 7.5,3 0)。根据直方图,这2 0 0名学生中每周的自习时间不少于2 2.5小时的人数是( )。

A.5 6 B.6 0 C.1 2 0 D.1 4 0

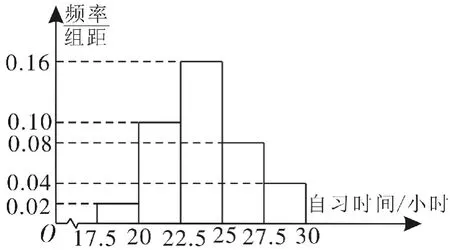
图1

解析：由频率分布直方图知,自习时间不少于2 2.5小时为后三组,有2 0 0×(0.1 6+0.0 8+0.0 4)×2.5=1 4 0(人),选D。

点评:本题主要考查频率分布直方图,是一道基础题目。从历年高考题目看,图表题已是屡见不鲜,作为一道应用题,考查考生的视图、用图能力,以及应用数学解决实际问题的能力。

例2 (2 0 1 6年高考山东文数)某儿童乐园在六一儿童节推出了一项趣味活动。参加活动的儿童需转动如图2所示的转盘两次,每次转动后,待转盘停止转动时,记录指针所指区域中的数。设两次记录的数分别为x,y。奖励规则如下:

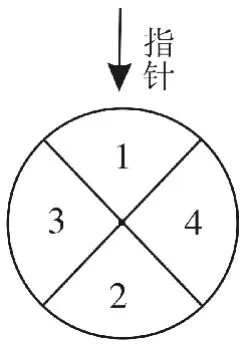
图2

①若x y≤3,则奖励玩具一个;

②若x y≥8,则奖励水杯一个;

③其余情况奖励饮料一瓶。

假设转盘质地均匀,四个区域划分均匀。小亮准备参加此项活动。

(Ⅰ)求小亮获得玩具的概率;

(Ⅱ)请比较小亮获得水杯与获得饮料的概率的大小,并说明理由。

解析：用数对(x,y)表示儿童参加活动先后记录的数,则基本事件空间Ω与点集S={(x,y)|x∈N,y∈N,1≤x≤4,1≤y≤4}一一对应。因为S中元素个数是4×4=1 6,所以基本事件总数为n=1 6。

(Ⅰ)记“x y≤3”为事件A。

则事件A包含的基本事件共有5个,即(1,1),(1,2),(1,3),(2,1),(3,1)。所以,P(A)=,即小亮获得玩具的概率为。

(Ⅱ)记“x y≥8”为事件B,“3＜x y＜8”为事件C。

则事件B包含的基本事件共有6个,即(2,4),(3,3),(3,4),(4,2),(4,3),(4,4)。

所以,P(B)=6=3。1 68

则事件C包含的基本事件共有5个,即(1,4),(2,2),(2,3),(3,2),(4,1),所以,P(C)=因为,所以,小亮获得水杯的概率大于获得饮料的概率。

点评:本题主要考查古典概型概率的计算。解答本题的关键在于准确确定所研究对象的基本事件空间、基本事件个数,利用概率的计算公式求解。本题较容易?,能较好地考查考生的数学应用意识、基本运算能力等。

二、面向社会生产实践

这类题突出在实践应用性上,注重社会现实,体现时代精神,试题选材体现社会热点,关注当前科技新发展。

例3 (2 0 1 6年高考新课标2理数)某险种的基本保费为a(单位:元),继续购买该险种的投保人称为续保人,续保人的本年度的保费与其上年度的出险次数的关联如下:

表1

设该险种一续保人一年内出险次数与相应概率如下:

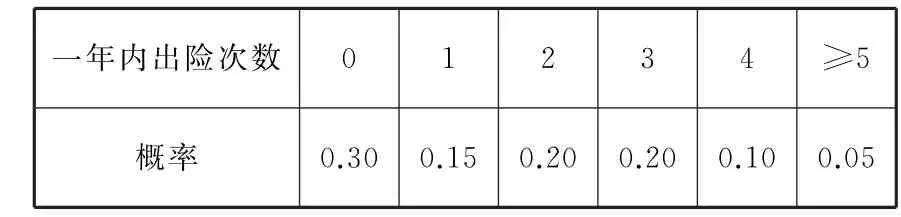
表2

(Ⅰ)求这一续保人本年度的保费高于基本保费的概率;

(Ⅱ)若这一续保人本年度的保费高于基本保费,求其保费比基本保费高出6 0%的概率;

(Ⅲ)求续保人本年度的平均保费与基本保费的比值。

分析：(Ⅰ)根据互斥事件的概率公式求这一续保人本年度的保费高于基本保费的概率;(Ⅱ)这一续保人本年度的保费高于基本保费,当且仅当一年内出险次数大于3,由条件概率公式求解;(Ⅲ)记续保人本年度的保费为X,求X的分布列,再根据期望公式求解。

解：(Ⅰ)设A表示事件:“这一续保人本年度的保费高于基本保费”,则事件A发生当且仅当一年内出险次数大于1,故P(A)=0.2+0.2+0.1+0.0 5=0.5 5。

(Ⅱ)设B表示事件:“这一续保人本年度的保费比基本保费高出6 0%”,则事件B发生当且仅当一年内出险次数大于3,故P(B)=0.1+0.0 5=0.1 5。

又P(A B)=P(B),故P(B|A)=因此所求概率为

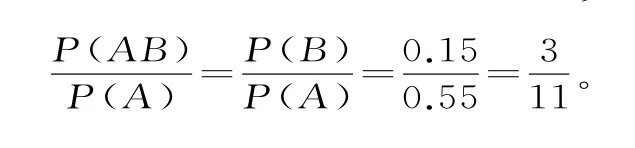
(Ⅲ)记续保人本年度的保费为X,则X的分布列为:

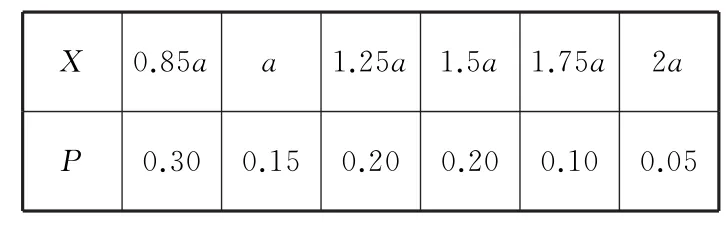
表3

E X=0.8 5a×0.3 0+a×0.1 5+1.2 5a×0.2 0+1.5a×0.2 0+1.7 5a×0.1 0+2a×0.0 5=1.2 3a。

因此续保人本年度的平均保费与基本保费的比值为1.2 3。

总结：条件概率的求法:

(1)定义法:先求P(A)和P(A B),再由

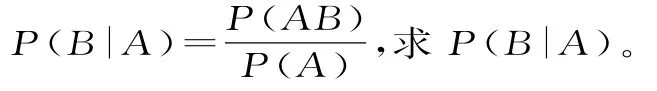
(2)基本事件法:当基本事件适合有限性和等可能性时,可借助古典概型概率公式,先求事件A包含的基本事件数n(A),再在事件A发生的条件下求事件B包含的基本事件数n(A B),得

求离散型随机变量均值的步骤:①理解随机变量X的意义,写出X可能取得的全部值;②求X的每个值的概率;③写出X的分布列;④由均值定义求出E(X)。

三、试题具有鲜明的时代特色

“使学生具有初步的创新精神”是新课程改革的核心理念之一,随着新课程改革的实施,新课标对数学学科的内容的学习有了新的要求,考试的内容也发生着变化,试题变得越来越新颖别致,具有鲜明的时代特色。

例4(2 0 1 6年高考天津理数)某小组共1 0人,利用假期参加义工活动,已知参加义工活动次数为1,2,3的人数分别为3,3,4,现从这1 0人中随机选出2人作为该组代表参加座谈会。

(Ⅰ)设A为事件“选出的2人参加义工活动次数之和为4”,求事件A发生的概率;

(Ⅱ)设X为选出的2人参加义工活动次数之差的绝对值,求随机变量X的分布列和数学期望。

分析：(Ⅰ)先确定从这1 0人中随机选出2人的基本事件种数:C210,再确定选出的2人参加义工活动次数之和为4所包含基本事件数:C13C14+C23,最后根据概率公式求出概率。(Ⅱ)先确定随机变量的可能取值为0,1,2,再分别求出对应概率,列出概率分布,最后根据公式计算数学期望。,所以,事件A发生的概率为

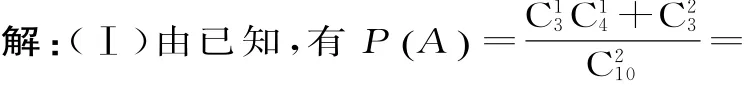
(Ⅱ)随机变量X的所有可能取值为0,1,2。所以,随机变量X的分布列为:随机变量X的数学期望E(X)

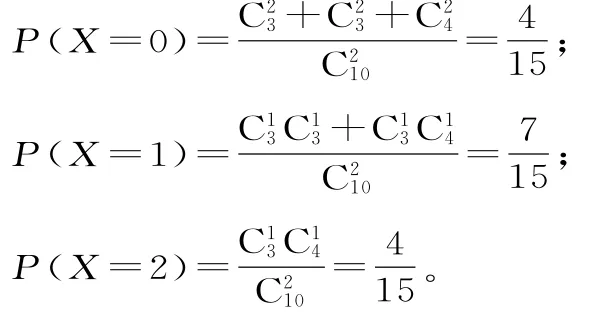
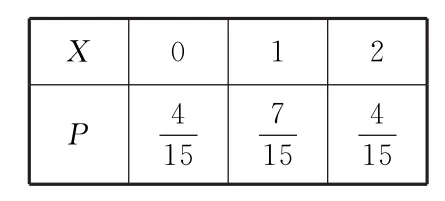
表4

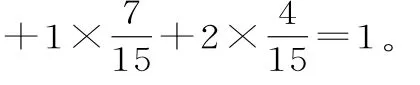
总结：求均值、方差的方法:

(1)已知随机变量的分布列求它的均值、方差和标准差,可直接按定义(公式)求解;

(2)已知随机变量ξ的均值、方差,求ξ的线性函数η=aξ+b的均值、方差和标准差,可直接用ξ的均值、方差的性质求解;

(3)如能分析确定所给随机变量是服从常用的分布(如两点分布、二项分布等),可直接利用它们的均值、方差公式求解。

四、图表信息题型的大量使用

2 1世纪是信息化社会,作为一个公民应学会搜索、整理和加工信息。表格、图像和图形是一种最直观、最形象的数学语言,包含着丰富的信息资源,如何观察、提炼这些信息,并利用这些信息来分析解决问题,是考查数学能力的较好形式之一。

例5 (2 0 1 6年高考新课标Ⅲ文数)某旅游城市为向游客介绍本地的气温情况,绘制了一年中月平均最高气温和平均最低气温的雷达图。图3中A点表示十月的平均最高气温约

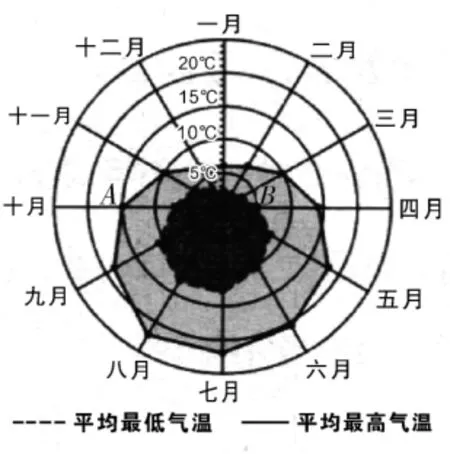
图3

为1 5℃,B点表示四月的平均最低气温约为5℃。下面叙述不正确的是( )A.各月的平均最低气温都在0℃以上B.七月的平均温差比一月的平均温差大C.三月和十一月的平均最高气温基本相同

D.平均气温高于2 0℃的月份有5个

解析：由图可知0℃均在虚线框内,所以各月的平均最低气温都在0℃ 以上,A正确;由图可知七月的平均温差大于7.5℃,而一月的平均温差小于7.5℃,所以七月的平均温差比一月的平均温差大,B正确;由图可知三月和十一月的平均最高气温都大约在5℃,基本相同,C正确;由图可知平均最高气温高于2 0℃的月份有3个或2个,所以D不正确。故选D。

点评:解答本题时易错点可能有两个:(1)对图形中的线条认识不明确,不知所措,只觉得是两把雨伞重叠在一起,找不到解决问题的方法;(2)估计平均温差时易出现错误,而错选B。