为数学点赞——为名师例析数学文化（5）统计与统计案例

■北京市教育学院丰台分院 张 琦

■北京市第十二中学高中部 高慧明

本刊特邀栏 介:

高慧明首 佳班主任,全国著名数学特级教师,国家教育部课程改革“全国先进工作者”,全国著名高考数学命题与考试研究专家,国家教育部“国培计划”全国中小学教师培训、班主任培训、校长培训特邀主讲专家,受邀在全国各地做有关高考科学备考、班级管理等多场专题报告。现任教于北京市第十二中学高中部。

随着时代的发展,对“管理”的要求也越来越高,除对客观现象进行定性分析以外,还需要进行相应的定量分析,这时候“统计”发挥着重要的作用。在对“统计”进行介绍之前,我们先来欣赏二战时期的数据分析故事。

第一则见于Cudmund R.Iversen和MaryGergen所著的《统计学——基本概念和方法》,故事如下。

第二次世界大战期间,盟军很想知道德军总共制造了多少辆坦克。德国人长于逻辑思维而乏于机变,在给坦克编号时非常刻板,他们把坦克从1开始编号。战争之中,盟军缴获了一些德军坦克,并记录下了它们的生产编号。这些编号对于了解德军的坦克总量有用处吗?在统计学家眼里,这些编号组成了一个样本,可由此去估计总的坦克数量。

制造出来的坦克数肯定不小于记录中的最大编号,为了推测它比缴获坦克中的最大编号大多少,可以先计算已知编号的平均值,并把这个平均值视为全部编号的中点。因此,样本均值乘以2就是坦克总数的一个估计,当然,这里必须存在一个假设:缴获的坦克代表了所有坦克的一个随机样本。使用这种方法估计,有可能出现一个荒谬的结果:作为全部坦克数量估计值的样本均值的2倍居然小于样本中的最大值。另一种估计方法是用观测到的最大编号乘以(1+1/n),如果缴获坦克数量为1 0,其中最大编号为5 0,那么坦克总数的一个估计是5 0×(1+1/1 0)=5 5。这种方法的各种变形的确用于二战之中。从战后发现的德军记录来看,盟军的估计值非常接近于德军生产坦克的实际值。记录还表明统计估计比其他情报方式所做的估计要大大接近于真实数目。统计学家做得比间谍们更漂亮!

第二则见于MichaelMorit在其Linkedin上发表的一篇有关数据挖掘在二战里运用的文章之中。

二战时狼群战术的发明者邓尼茨在一战时期就是一名潜艇指挥官,被俘后在战俘营想出了狼群战术。狼群战术主要核心就是当一艘潜艇发现目标后立即通知潜艇指挥部,把敌人的速度、航行、数量等情况说明。潜艇指挥部立即发报命令目标周围的潜艇赶去支援和攻击,这样可以大大提高攻击成功率,最大地杀伤敌人(潜艇多,携带的鱼雷就多),减少己方的危险性。狼群战术在二战残酷的海战中证明是一种有效的战术,特别是邓尼茨当上潜艇司令官后。如果不是美国在关键时候伸出援手支持了英国,很有可能英国就会被小小的潜艇打败。丘吉尔在战时对潜艇的一番评价最有说服力:“我们的脖子快被这些小家伙掐断了!”

盟军货船被德国潜艇狼群战术弄得苦不堪言,但海军与空军将领在很长的一段时间内都拒绝改变他们的信条——小编制比大编制更安全,尽管有着铁证证明这是错误的。Blackett证明了在一个有1 5～2 4艘船的舰队中,每艘船有2.3%的概率被击沉;而在舰队船只数量高于4 5时,被击中的概率只有1.1%。

欣赏完这两则故事,也许大家对统计的重要作用有了初步的认识。那么,什么是统计呢?如果理解为动词,就是对一系列的数据进行分析处理;如果理解为名词,那可以简单理解为统计学,统计学是一门具有方法论性质的应用性科学,它在概率论基础上,发展出一系列的原理和方法,研究如何采集和整理反映事物总体信息的数字资料,并依据这些复杂的数据(称为样本)对总体的特征和现象背后隐藏的规律进行分析和推断。

法国数学家拉普拉斯有句名言:“生活中最重要的问题,绝大部分其实只是概率问题。”我们看个具体例子,给定一根木棒,谁都不会怀疑它有自身的“客观”的长度,长度是多少?我们可以用各种仪器去测量,但是不管我们的仪器多么精确,你得到的数据也总是稳定在木棒真实长度的附近。事实上,我们日常中不就是把测量所得的值当作真实的“长度”而进行各类应用吗?

我们现在再来看看《普通高中数学课程标准(2 0 1 7年版)》对这部分内容的要求:“数据收集和整理的方法、数据直观图表的表示方法、数据统计特征的刻画方法”和“样本相关系数的统计含义,了解一元线性回归模型和2×2列联表,运用这些方法解决简单的实际问题”。从思想上来讲,需要同学们“通过具体实例,感悟在实际生活中进行科学决策的必要性和可能性;体会统计思维与确定性思维的差异、归纳推断与演绎证明的差异”。《普通高中数学课程标准(2 0 1 7年版)》对高中阶段教学内容进行这样的要求,是有其历史原因和现实背景的,下面我们就对其历史进行简单的梳理和介绍。

一、统计学的产生初期

统计学是随着统计的产生而产生的,而统计作为一种社会实践活动已有悠久的历史。在中国,夏禹时代就有了人口数量的记载;为了赋税、徭役和兵役的需要,历代都有田亩和户口等记录。在国外,古巴比伦、埃及和罗马帝国也有人口和资源的详细记录;到中世纪,西欧各国都有人口、军队、领地、职业、财产的统计。

比如被誉为古代数学“算经十书”(汉唐之间出现的十部古算书)之首的《九章算术》就蕴涵着丰富的统计思想和统计理念。例如统计分组、线性拟合、抽样推断、加权平均等。

我国古代数学名著《九章算术》衰分章十七问为“生丝干耗”问题:“今有生丝三十斤,干之,耗三斤十二两。今有干丝一十二斤,问生丝几何。”

本题中以生丝三十得干丝过程损耗重量计算可得所谓“干丝率”,其实就是以此作为一个抽样,并以该抽样的平均数(即干、生丝的比值)来推断总体,也就是所有生丝所能获得干丝的比例,之后以该比例解决其他重量的生、干丝关系问题。暗含了以此个体数据作为整体通例数据的思想,抽样推断的痕迹十分明显。

在应用统计学进行抽样的时候,问卷的设计是一门很大的学问。特别是对一些敏感性问题,即使调查是无记名的,也会使被调查者感到尴尬,从而使得结果与实际情况出入比较大。

这时候,我们就可以设计如下方案可使被调查者愿意作出真实的回答:在一个箱子里放进1个红球和1个白球。被调查者在摸到球后记住颜色并立刻将球放回,然后根据球的颜色是红和白分别回答如下问题:你的生日是不是奇数?你是否有过偷税漏税行为?回答时只要在一张预备好的白纸上写下是或否。假定被调查者有2 0 0人,统计出共有5 8个是。

由题意可知,每个人从箱子中摸出1个白球或红球的概率都是0.5,也就是我们期望大约有1 0 0个人回答了第一个问题,另1 0 0个人回答了第二个问题。在摸出红球的情况下,答是的概率为0.5。因而大约有8个人回答了关于偷税漏税的问题。我们可以估计大约有8%的人有过偷税漏税行为。

上述问题的概率解释为,已知P(红)=0.5,P(是|红)=0.5,P(是)=0.2 9,求条件概率P(是|白),用概率论中的贝叶斯公式算出的答案是8%。

二、统计学的发展时期

概率论起源于中世纪的欧洲,那时盛行掷骰子赌博,人们提出了许多有趣的概率问题。当时法国的帕斯卡、费尔马和旅居巴黎的荷兰数学家惠更斯都对此类问题感兴趣,他们用组合数学研究了许多与掷骰子有关的概率计算问题。

概率论是统计推断的基础,是在给定数据生成过程下观测、研究数据的性质;而统计推断则根据观测的数据,反向思考其数据生成过程。预测、分类、聚类、估计等,都是统计推断的特殊形式,强调对于数据生成过程的研究。概率论大数定律的三个定理就是要说明为什么样本均值可以估计总体均值,而这个估计的准确性却是要由统计学说了算。对于各种分布的参数估计,之后的模拟估测,虽然与概率论看似完全无关,实际上却是由它们在支撑着统计学这个科目。这个情况对于参数统计、非参数统计、半参数统计,都是一样的。

我们来看一个有关概率的案例——生日悖论:

众所周知,在生活中,如果能够遇到与自己同一天生日的人,我们大多会很惊喜,觉得这种缘分似乎很少见,又或者说这是一个很小的概率。那我们是否有想过,假如在2 3个人当中,出现两个人是同一天生日的这种缘分的概率有多大呢?是5%?1 0%?还是2 0%?又或者是更多呢?下面我们一起来看看。

文章开始我们不想长篇大论地把很多公式给搬上来,那样没意思,吊足了大家的胃口,却不受待见。所以,在开始的时候,我们就不打算写那么多计算过程,留着后面慢慢讨论和解释。那么告诉各位:2 3个人中,有两个人生日是同一天的概率约为5 0%(甚至比这个数值还高出那么一点点),在5 0个人中有相同生日的概率,竟然高达9 7%,这两个数值,这两个结果,各位是不是有点不太敢相信?

其实这个结果并没有算错,是有理有据的,只是我们的直觉错了,科学与生活,就好比梦想和现实一样:梦想往往是丰满的,现实呢,却常常是骨感的。正因为经过科学方法计算出来的结果与我们日常生活的经验产生了如此大的落差,所以我们把这类问题称为“生日悖论(B i r t h d a yP a r a d o x)”。

在分析时,我们不把某一年有2月2 9日或者某两人是双胞胎这样的或者类似的外界因素算在内,只考虑纯粹的随机概率,也就是说每个人出生的日子都随机分布在一年3 6 5天的任何一天。同时假设如果此时有n个人在同一房间内,要计算至少有两个人生日是同一天的概率,假设一年3 6 5日出生概率是平均分布的(虽然在现实生活中,出生时间并不是平均分布的)。下面我们运用数学知识来慢慢解答和计算:

首先,假设P(n)代表n个人中每个人生日都不一样的概率,前面说了,n不能大于3 6 5,故0≤n≤3 6 5,那么P(n)为:

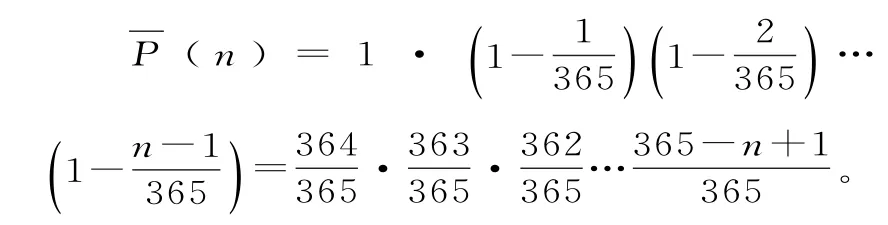
第一个人的生日是3 6 5天的其中一天,假设是一定的,是不变的,那么第二个人不能跟第一个人有相同的生日的概率就是

理第三个人不能跟前两个人生日相同,依此类推。很容易用阶乘写成如下形式

如果P(n)表示n个人中至少2人生日相同的概率,那么:

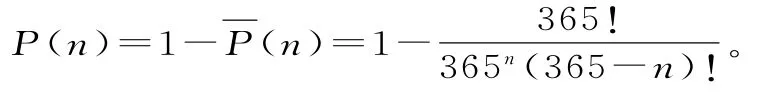
当n≥3 6 5时P(n)=1是必然的。当n=2 3时,代入公式得,概率大约是0.5 0 7。其,同他数字的概率用上面的算法可以近似地得出来,这里我们从网上下载了一张图表(表1),我们可以大致感受下其变换过程:

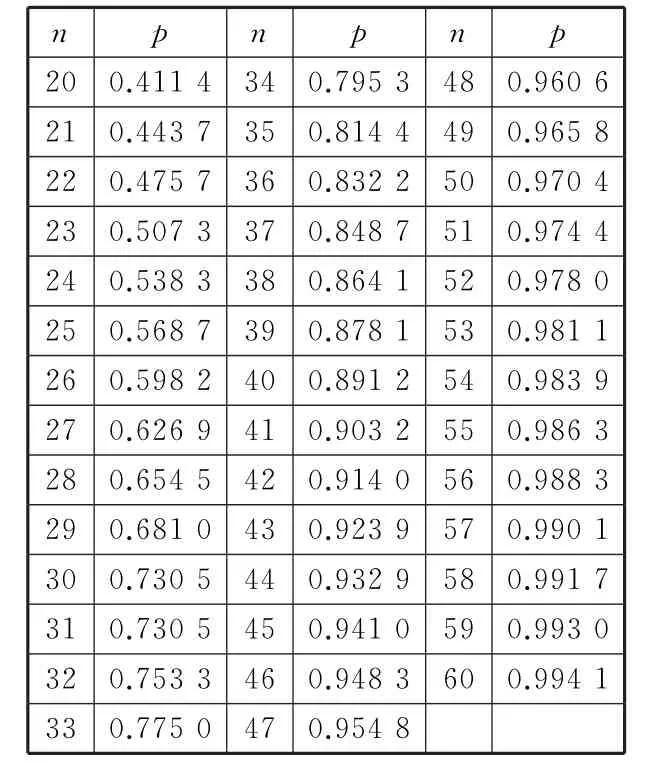
表1

从上表可以看出,当n为4 1人是就已经超过了9 0%,4 7人时就已经超过了9 5%了。为什么实际情况与我们想象的差别这么大呢?我们把问题稍作改动,就能得到启发。新的问题是:在一群人当中,有人与你同一天生日,这个概率有多大?仔细想想,这个问题还是比较简单的。记p(n)表示房间中n个其他人中与特定人(比如你)有相同生日的概

有大约0.0 5 9,约高于十七分之一。如果n个人中有5 0%概率存在某人跟你有相同生日,n至少要达到2 5 3,注意这个数字大大高于

所以,“生日悖论”产生的原因就是因为当我们看到“有人生日相同”时,下意识地用“与我生日相同”去推测,以至于把火箭发射当成了平稳增长,造成了生日悖论。到了这里,大家是否对“生日悖论”有了更深一步的了解呢?所以生日悖论的本质其实就是,随着元素的增多,出现重复元素的概率会以惊人的速率增加,但是我们往往低估了它的速率。

三、统计学的成熟时期

2 0世纪初以来,科学技术迅猛发展,社会发生了巨大变化,统计学进入了快速发展时期。归纳起来有以下几个方面。

由记述统计向推断统计发展。记述统计是对所搜集的大量数据资料进行加工整理、综合概括,通过图示、列表和数字,如编制次数分布表、绘制直方图、计算各种特征数等,对资料进行分析和描述。而推断统计,则是在搜集、整理观测的样本数据基础上,对有关总体作出推断。其特点是根据带随机性的观测样本数据以及问题的条件和假定(模型),而对未知事物作出的,以概率形式表述的推断。目前,西方国家所指的科学统计方法,主要就是指推断统计来说的。但受到高中知识所限,我们现在所学内容还只限于记述统计。

计算技术和一系列新技术、新方法在统计领域不断得到开发和应用。近几十年,计算机技术不断发展,使统计数据的搜集、处理、分析、存贮、传递、印制等过程日益现代化,提高了统计工作的效能。计算机技术的发展,日益扩大了传统的和先进的统计技术的应用领域,促使统计科学和统计工作发生了革命性的变化。如今,计算机科学已经成为统计科学不可分割的组成部分。随着科学技术的发展,统计理论、实践深度和广度方面也不断发展。

受高中知识所限,我们不对最新统计知识进行介绍,而是再来欣赏三则统计悖论。

第一则案例——猜奖游戏:

这一问题出自美国的一个电视游戏节目,问题的名字来自该节目的主持人蒙提·霍尔。上世纪9 0年代曾在美国引起广泛和热烈的讨论。

假定在台上有三扇关闭的门,其中一扇门后面有一辆汽车,另外两扇门后面各有一只山羊。主持人是知道哪扇门后面有汽车的。当竞猜者选定了一扇门但尚未开启它的时候,节目主持人去开启剩下两扇门中的一扇,露出的是山羊。主持人会问参赛者要不要改猜另一扇未开启的门。

解决问题的关键是改猜另一扇未开启的门是否比不改猜赢得汽车的概率要大。正确的答案是:改猜能增大赢得汽车的概率,从原来的1/3增大为2/3。这是因为竞猜者选定的一扇门后面有汽车的概率是1/3,在未选定的两扇门后面有汽车的概率是2/3,主持人开启其中一扇门把这门后面有汽车给排除了,所以另一扇未开启的门后面有汽车的概率是2/3。

第二则案例——“统计平均”的陷阱:

假定某大学数学系有教授1 5人、副教授4 0人、讲师和助教2 5人,这三类人的平均年收入分别是1 5万、1 2万、8万,该单位职工平均年收入为1 0万。又假定科学院某研究所有研究员6 0人、副研究员3 0人、助研3 0人,这三类人的平均年收入分别是1 4万、1 1万、7万,但该研究所职工平均年收入为1 1.5万,高出那个系职工平均年收入1.5万。这一例子表明:由于各单位人员构成比例不同,单位职工平均年收入这一指标不能真实反映单位职工的收入状况。

第三则案例——“辛普森悖论”:

看下面例子。假定有两种药(A和B),要通过分组临床试验对比其疗效。表2是试验结果的统计表。从甲乙两组试验结果看,药物A的疗效都优于药物B,但总体来看,药物B的疗效反而优于药物A(如表2所示)。

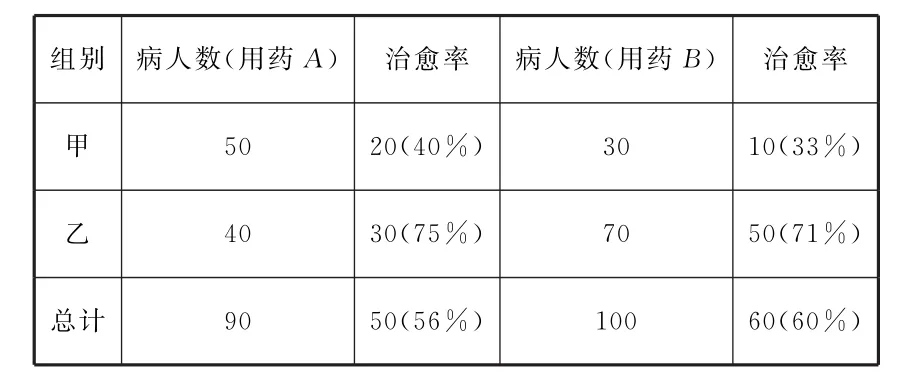
表2

早在2 0世纪初,人们就发现了这种现象:在分组比较中都占优势的一方,在总评中反而是失势。直到1 9 5 1年英国统计学家辛普森在他发表的论文中才正式对这一现象给予理论解释。后人就把这一现象称为“辛普森悖论”。

理论上该如何解释呢?

在最后总计A和B的治愈率时,实际上是对A和B治愈率按用药率进行加权平均,即:

总计A的治愈率=甲组A的治愈率×甲组A的用药率+乙组A的治愈率×乙组A的用药率。

总计B的治愈率=甲组B的治愈率×甲组B的用药率+乙组B的治愈率×乙组B的用药率。

在这里的权数是用药率。

按表2中所给数据,具体算式是:

不难发现,药物A的疗效都优于药物B,但总体来看,药物B的疗效反而优于药物A。可见,悖论的产生是由于“权重”的不同倾斜。在计算A的治愈率时,用药率高的甲组的权重大,用药率低的乙组的权重小;而在计算B的治愈率时,用药率高的乙组的权重大,用药率低的甲组的权重小。至于是什么原因引起权重的这种倾斜,则需要具体问题具体分析。

统计在现代化管理和社会生活中的地位日益重要。随着社会、经济和科学技术的发展,统计在现代化国家管理和企业管理中的地位,在社会生活中的地位,越来越重要了。人们的日常生活和一切社会生活都离不开统计。英国统计学家哈斯利特说:“统计方法的应用是这样普遍,在我们的生活和习惯中,统计的影响是这样巨大,以致统计的重要性无论怎样强调也不过分。”甚至有的科学家还把我们的时代叫作“统计时代”。显然,2 0世纪统计科学的发展及其未来,已经被赋予了划时代的意义。

事实上,统计学产生于应用,在应用过程中发展壮大。随着经济社会的发展、各学科相互融合趋势的发展和计算机技术的迅速发展,统计学的应用领域、统计理论与分析方法也将不断发展,在所有领域展现它的生命力和重要作用。