EM算法在闪烁噪声分布参数估计中的应用
李广柱 陈威兵 李 玮 张刚林 苏 钢
(长沙学院 长沙 410022)
0 引言
近距离跟踪雷达,目标回波具有角闪烁特性,如果处理不当,会增加雷达跟踪目标的误差,甚至会丢失目标。目标角闪烁噪声的分布是非高斯的,具有较长的拖尾[1-5]。在实际应用时,常采用高斯分布和较小概率出现的大方差拉普拉斯分布噪声混合进行建模,该分布模型是研究跟踪滤波算法的重要基础[6-7]。
本文专门研究角闪烁噪声的分布参数估计,基于混合分布模型,采用EM算法估计分布参数,给出了分布参数估计的理论推导,列出了参数估计的计算流程,并进行了仿真验证。理论推导和仿真结果表明,采用EM算法可以估计得到混合分布模型的参数。
1 闪烁噪声分布参数的EM估计算法
1.1 角闪烁噪声的混合分布模型
角闪烁噪声,一般认为服从混合分布模型为
f(x;σ,η,ε)=(1-ε)fg(x)+εfl(x)
(1)
式(1)中fg(x)、fl(x)分别表示高斯分布和拉普拉斯分布的概率分布函数,ε≪1是观测噪声服从拉普拉斯分布的概率。其中
(2)
(3)
式(2)、式(3)中σ、η分别为高斯分布、拉普拉斯分布的参数。
1.2 EM分布参数估计算法
假设有采样序列x=[x0,x1,…,xN-1]T,服从上述混合分布模型,可知序列x的概率分布为
(4)
式(4)中的α为服从[0,1]分布的随机数,且α=1的概率为ε。可知似然比函数为
L(θ)=lnf(x|σ,η,ε)
(5)
似然比函数的数学期望为

(6)
式(6)中的Θ为待估计参数的集合,Θ(k)表示第k次迭代时的参数值;p(xn|g;θ)、p(xn|l;θ)分别表示在参数θ=[σ,η,ε]T的条件下,xn分别服从高斯分布和拉普拉斯分布的概率;Pg、Pl分别表示样本服从高斯分布和拉普拉斯分布的概率;P(g|xn)和P(l|xn)表示当采样值为xn的时候,分别服从高斯分布和拉普拉斯分布的概率。将式(1)带入式(6)可得混合模型条件下Q(Θ;Θ(k))的表达式。可知,分布参数θ=[σ,η,ε]T的似然估计在Q(Θ;Θ(k))的极值处取到。求Q(Θ;Θ(k))对θ=[σ,η,ε]T的导数可得
(7)
令式(7)等于0,可得θ=[σ,η,ε]T的似然估计为
(8)
为了完成迭代的运算,还需引入P(g|xn)和P(l|xn)的更新
(9)
利用式(8)和式(9),可以通过迭代的方式得到θ=[σ,η,ε]T的估计,下面介绍具体的实现算法。
2 分布参数估计的算法流程
基于式(8)和式(9),可得到采用EM算法估计闪烁噪声的分布参数的计算流程如下:
1)Step1,设定k=1时,分布参数的初始值θ(1)=[σ(1),η(1),ε(1)]T,可容忍的迭代次数K和可接受的迭代误差δ;
2)Step2,对于第k+1次迭代,计算:
(10)
3)Step3,按式(9)计算P(g|xn)(k+1)和P(l|xn)(k+1);
4)Step4,按式(8)计算θ(k+1)=[σ(k+1),η(k+1),ε(k+1)]T;

3 仿真实验
在实际应用的时候,可以采集近距离跟踪雷达在跟踪目标过程中的观测噪声,采用EM算法对角闪烁噪声的分布参数进行估计。本文采用仿真的方法验证EM算法的有效性,改变仿真时采用的角闪烁噪声的分布参数,通过对比仿真用到的分布参数和EM算法的估计结果,可以验证算法的有效性。
选取参数σ2=1、η=3、ε=0.05,仿真得到长度为4096点的角闪烁噪声序列。设置分布参数的初始值为:σ2(1)=0.5、η(1)=1、ε(1)=0.1,可容忍的迭代次数K=500;可接受的迭代误差δ=10-7。采用EM迭代算法进行估计,得到的估计结果如图 1所示。图 1给出的是相对误差,故纵坐标的单位是%。

图1 EM算法估计噪声分布参数的相对误差
由图 1可见,迭代40次左右即可达到较好的效果。为了验证EM算法估计的可重复性,本文模拟了500组相同分布参数的角闪烁噪声序列,利用EM算法估计得到分布参数:σ2、η、ε的频数分布直方图,如图 2到图 4所示。

图2 参数σ2估计值的频数分布直方图

图3 参数η估计值的频数分布直方图
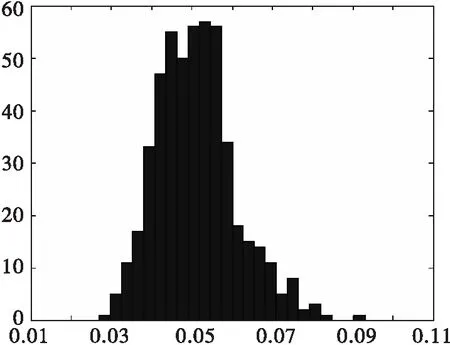
图4 参数ε估计值的频数分布直方图
通过图2到图4可以发现,η,特别是ε的估计值有较长的拖尾,为此对σ2、η和ε的估计值进行Jarque-Bera分布检验,结果如表 1所示。

表1 估计值的Jarque-Bera检验
表1采用的置信度为0.05,表中h表示是否接受样本服从高斯分布:h=0,表示样本服从高斯分布;h=1,表示样本不服从高斯分布,由表 1可以看出,σ2的估计值服从高斯分布,η和ε不服从高斯分布。表中p为Jarque-Bera检验统计量,p小于置信度,说明估计值不服从高斯分布,由表 1可见,η、ε的Jarque-Bera检验统计量皆小于置信度,其中ε的Jarque-Bera检验统计量很小,这与图 4是吻合的。
表2给出σ2、η和ε估计值的前两阶矩的计算结果。

表2 500次估计值的均值和标准差
通过表 2可以发现,采用EM算法估计混合分布模型的参数σ2和ε的效果较好,参数η的估计标准差略大,这是由于ε较小,模拟得到的角闪烁噪声序列中服从拉普拉斯分布的噪声点少,样本数较少造成的。因此,可以通过提高总的观测样本来提高参数η的估计精度。
4 结束语
角闪烁噪声是影响近距离跟踪雷达性能的重要因素,掌握它的概率分布是改善目标跟踪性能的重要依据。本文提出采用EM算法估计角闪烁噪声的分布参数,推导了理论模型,列出了计算流程,并进行了仿真。通过仿真发现,EM算法能够估计得到角闪烁噪声的分布参数,其中σ2的估计值服从高斯分布,η和ε不服从高斯分布;计算结果表明,σ2、η和ε估计值的均值与真值偏差小,综合分析可以认为算法效果良好。下一步可以通过半实物仿真和实物仿真,估计得到角闪烁噪声的分布参数。

