雷达测量时间误差检测方法研究
闫永宝 刘小东 刘明通 张 亮
(中国人民解放军61191部队 杭州 310023)
0 引言
雷达主要用于目标的搜索、捕获和跟踪,测量精度要求高。时统设备作为雷达的统一时间基准,发挥着重要的作用,时统采用高稳定频率源,利用GPS、北斗和其他授时信号作为时统源标校本地时间基准,一旦时统产生时间误差,将会导致测量数据误差偏大,数据无法使用,严重影响雷达正常工作[1-4]。测量时间误差的计算需要找到比时统时间更精准的时标,在现实雷达系统中是无法找到的,这将是制约计算测量时间误差的关键因素[5-7]。本文针对时统设备异常时导致的时间误差问题,提出一种间接检测测量时间误差的方法,应用表明,方法是有效的。
1 方法原理
雷达测量精度主要包括方位角、俯仰角和斜距测量精度。测量精度一般用测量误差来表示,按照误差的特点与性质,误差可分为系统误差、随机误差和粗大误差三类。其中,雷达的粗大误差主要体现在没有回波的预测点位,比例很少,可以通过回波幅度值是否为零来判断剔除。系统误差和随机误差是测量精度计算的主要研究对象。
定义雷达测量误差为:“观测值-理论值”。观测值为雷达在地平坐标系下的在时间上不等间隔的位置坐标测量数据,真值取标校星精密星历,是一组在地固坐标系下的在时间上等间隔的位置坐标,坐标精度可以达到米级,通过把精密星历的时刻对齐到雷达测量时刻,而后将坐标转化为雷达地平坐标系下的数值,将该精密星历数值作为“理论值”。观测值减去理论值的结果即为雷达测量误差,通过对斜距误差做统计,如果雷达斜距误差某一次明显偏大,则说明测量时间可能存在误差,此时将精密星历数据斜距对齐到测量数据,通过对时间做差得到时间误差。
1.1 雷达测量数据单个点位误差计算
卫星精密星历数据是地固坐标系下的在时间上等间隔的位置坐标,雷达的观测数据是地平坐标系下的在时间上不等间隔的位置坐标。因此需要对卫星精密星历数据进行插值处理,使得时间上一致,插值算法选用9阶拉格朗日插值法
(1)
Ln(x)插值计算的结果,x为插值计算结果对应的时刻。
由于卫星精密星历是在地固坐标系下描述的,雷达实测数据是地平坐标系下描述的,两者不一致,需要进行坐标转换,将对应时刻的星历转换到地平坐标系中。

图1 坐标转换示意图

(2)
其中,φ、λ为测站大地纬度和经度。
另外,还需要将直角坐标转换到极坐标(方位角、俯仰角和斜距),转换关系为
(3)
从而得到单个点位的测量误差为
δi=Oi-Ci
(4)
1.2 雷达测量数据单条弧段精度计算
雷达测量数据单条弧段每个点误差的算术平均值作为该测量弧段的系统误差,定义为
(5)
随机误差也称为标准差,也可称之为均方根误差,定义为
(6)
数据综合精度计算方法为
(7)
1.3 雷达测量精度计算
以一段时间内计算得到的雷达测量数据单条弧段数据综合精度为样本,计算得到算术平均值作为该时间段内雷达的测量精度为
(8)
随机误差为
(9)
σ1rad是雷达在该时间段内的测量精度,σ2rad反映的是测量精度波动程度,σ2rad越小,说明测量精度变化越小,σ2rad越大,说明测量精度变化越大。
1.4 雷达测量时间误差计算
当雷达时统出现较大误差时,会在雷达测量精度上间接反映出来。计算表明,当雷达测量时间误差为1s时,反映在斜距上的测量误差可以达到千米级。
参考雷达测量精度的计算方法,采用9阶拉格朗日插值法,使得斜距上一致。则单个测量点位的时间误差见式(10)。
δti=Oti-Cti
(10)
Oti为单个测量点位的测量时间,Cti为理论时间,以测量弧段上的全部点位对应的时间误差为研究对象,计算其算数平均值即为雷达在这条弧段的时间误差。
(11)
在实际应用中,偶然出现一次时间误差偏大时,不能认定为时统产生时间误差,有可能是野值或是目标轨道机动,在此引入数理统计的思想,以雷达能够搜索的目标NORAD双行根数为样本,将雷达搜索的目标进行匹配识别,而后得到时间误差,对一段时间的目标时间误差做统计分析,即可判断时间误差是否出现异常。
2 方法验证
对同一次时间误差超限事件进行算法验证。第一种采用激光测距卫星精密星历作为参考计算测量时间误差,从图2、图3可以看出,测量时间正常时,时间误差均值为-0.0055 s,第77天开始,测量时间误差达到0.1984 s,二者差值为0.2039 s,对应的斜距误差达到约553 m,与理论推算结果基本一致。
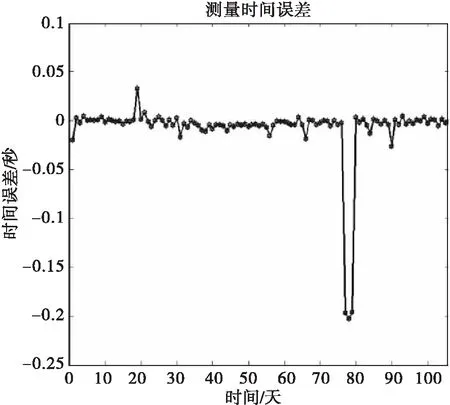
图2 测量时间误差

图3 测量斜距误差
第二种采用1879个空间目标的NORAD双行根数作为参考计算时间误差。结果如图4所示,从图中可以看出,测量时间异常时时间误差明显抬升,时间误差均值为0.1068 s;测量时间正常时,时间误差均值为-0.096 s,二者差值接近0.2028 s,与采用精密星历计算的时间误差基本一致。
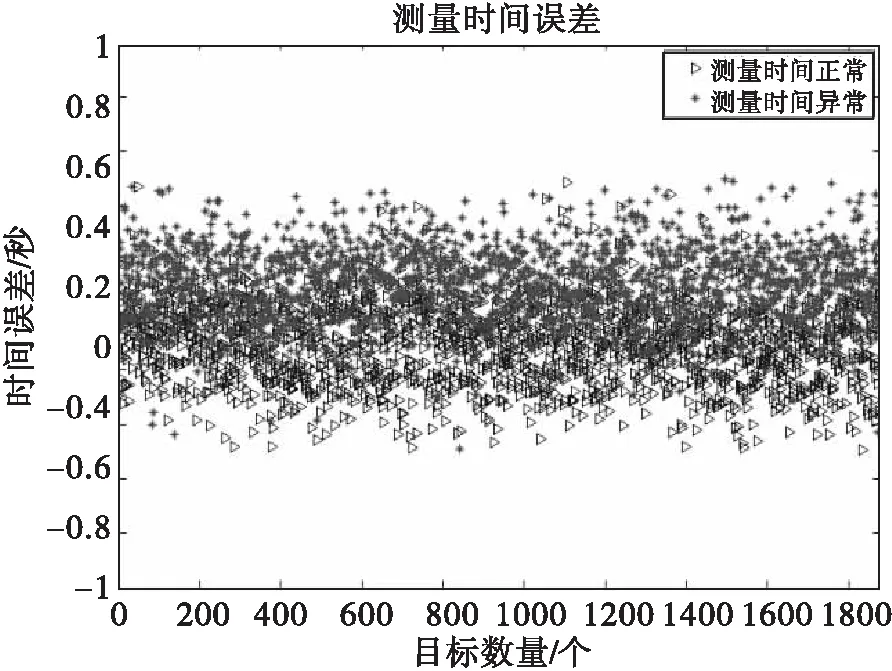
图4 测量时间误差
从上述两种方法可以看出,采用精密星历计算的测量时间误差可判断误差超过0.01 s的异常;采用目标NORAD双行根数计算的时间误差可判断误差超过0.1 s的异常。验证结果符合轨道理论分析。
3 结束语
本文提出了一种新的雷达测量时间误差检测方法,并对雷达测量精度和时间误差定义进行描述,最后分别采用激光测距卫星精密星历和目标NORAD双行根数两种方法对雷达某次测量时间误差超限事件进行统计分析,分析结果表明,采用精密星历计算测量时间误差可以检测误差小于0.01 s的时间误差;采用目标NORAD双行根数计算测量时间误差可以检测误差小于0.1 s的时间误差,并能以数理统计思想描述误差趋势。两种方法计算结果一致,并成功检测出雷达的时统异常问题。

