让复习充满思维的张力
———以一年级上册“数与代数”总复习为例
◇位惠女
如何带领一年级的学生进行总复习,一直以来都是老师们比较困惑的问题。不少老师认为,一年级学生年龄小,不具备复习的能力,在进行学期总复习的时候,老师们习惯性地按照教材上的问题,逐一呈现给学生,学生表达一下自己的想法,完成一定量的习题,就算完成了复习的任务。
事实如何呢?如果我们给学生时间和空间,学生会有什么样的表现?结合北师大版教材一年级上册“数与代数”总复习的内容,我带领学生进行了尝试,学生思维的张力出乎我的意料。
在“数与代数”领域的复习中,教材设计了两个栏目:一是独立思考,主要是结合一些提示性问题,引导学生对本学期学习的主要内容进行回顾与整理,沟通知识之间的内在联系,让学生在这个过程中学习如何对自己所学知识进行归纳、整理,初步感受归纳、整理的数学思想;二是相互启发,主要是针对“独立思考”中提出的问题,有选择地进行启发性的交流,引导学生从不同角度思考问题。
根据以上思考,我制订了以下学习目标:1.经历对本学期“数与代数”领域所学内容进行梳理的过程,初步养成回顾与反思的良好习惯;2.进一步认识20 以内的数,能正确计算10 以内数的加减法、20 以内数的进位加法和不退位减法;3.能运用学过的知识解决相关的简单问题。
好玩的数
课始,教师抛出一个问题:举例说一说,对于数,你有哪些认识?可以写一写,画一画。小组讨论后全班进行交流。
师:谁来和大家说说自己的想法?
生1:我们组有6个人,从前往后数,我排第1个;从后往前数,我排第6个,很好玩的。
生2:我发现 1个人和 1群人都可以用1 来表示。
生3:是啊,1 可以表示 1个很小的物体,也可以表示1个很大的物体,比如1 棵小草、1座大山都可以用1 来表示。
生4:我还发现 1 站在不同的位置,表示的大小也不同。
师:这是一个非常棒的发现,能具体来说一说吗?
生4:(如图 1)1 放在个位上,表示的是1个一,1 放在十位上,表示的是1个十。
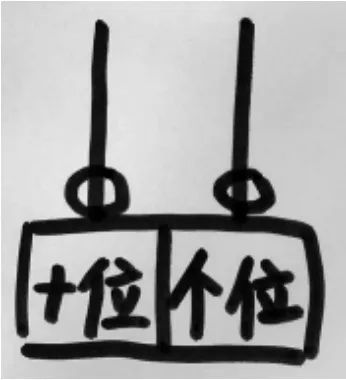
图1
生5:我补充,要是放在百位上,就表示1个百啦。
师:是啊,数放在不同的数位上,表示的意义是不同的。你能想办法说明15 和6 谁大吗?
生1:当然是 15 大了,因为15 在9 的右面,我是画尺子进行说明的。(如图2)
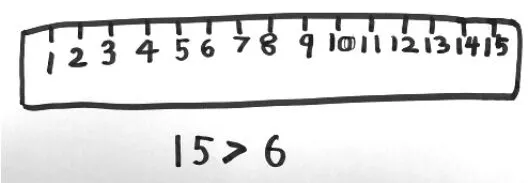
图2
生2:我用15个圆圈表示15,用 6个三角形表示 6,排成两排,一个圆圈对应一个三角形,发现圆圈多了好多,所以15>6。(如图 3)

图3
生3:我是这样表示的,一条表示10,加上5个单独的方块表示15,另一边只有6个单独的方块,所以6比15小。(如图 4)

图4
生4:还可以在计数器上表 示 ,15表示1个十和5个一,6 只有 6个一,所以 15>6。
师:大家的想法真好,让别人一听就明白为什么15 比6大。下面有个更有挑战性的问题,我们一起来看一下。(如图5)

图5
生1:我是这样表示的,用一个大蘑菇表示10,用两个小蘑菇表示2,就是12 了。(图略)
生2:我是用一个大方框表示10,用两个小方框表示2,这样就可以表示12 了。(图略)
生3:我是用计数器表示的,十位上的 1 颗珠子表示 1个十,个位上的2 颗珠子表示2个一,合起来就是12 了。
师:很好的思路,小组讨论一下,试着根据刚才的讨论过程画一个思维导图。有困难的可以举手,老师来帮助你们。
(学生讨论,尝试绘制关于数的思维导图,教师巡视并进行指导)
师:哪个小组先来和大家交流一下?
组1:我们小组是以 2 为例来画的,我们想到了2个三角形可以用2 表示,2个苹果、2 筐苹果都可以用2 来表示,2大于1,2 放在十位上表示2个十。(如图 6)

图6
组2:我们小组是以 10 为例来画的,我们认为10 是个很重要的数,1 盒笔有 10 支,可以用 10个圆圈表示 10,10 比1 大,10 可以表示 1个十,还可以表示10个一。(如图7)
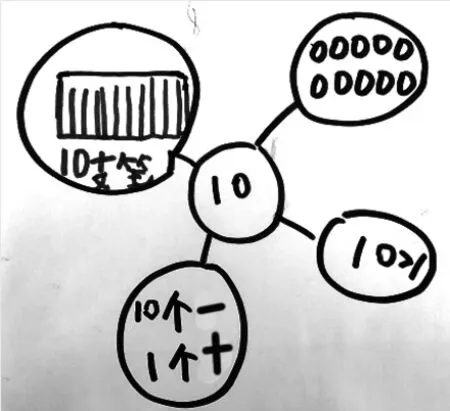
图7
随着讨论的深入,学生的思路在不断地向深处蔓延,他们从“1”出发,不仅举出了生活中的例子,感受到数可以用来表示数量和顺序,能用自己的语言描述1 站在不同的位置,表示的大小也不同,体会到了位值的概念。在比较15 和6 谁大时,学生不同的表示方法,不仅仅是在比较数的大小,还包括用自己的方式诠释对比较方法的理解。特别是学生尝试用思维导图表示对数的认识的理解,基本上能从不同的角度体现对数的理解,这表明一年级的学生已经初步具备了梳理、整理、归纳的能力。
有趣的问题
在学生复习了数的认识后,教师带领学生进行数的运算的复习。教师先抛出课本上的一个问题(如图8),鼓励学生提出数学问题,并由此展开学习过程。

图8
师:你能提出哪些数学问题?
生1:一共得了几颗星?
生2:数学作业比语文作业少几颗星?
生3:语文作业比数学作业多几颗星?
师:请你选择一个问题进行解决,并说说你是怎么算的。
(学生根据教师板书的问题,选择问题进行解决,并写出自己的计算方法,教师巡视并进行指导)
师:谁来和大家说说你的想法?
生1:我选择的是第 1个问题,这道题用加法完成,因为是求合起来一共是多少,我列出的算式是 9+7=16(颗)。
师:谁和他选择的问题一样?(不少学生举手示意)有补充的吗?
生2:我想补充一下9+7是如何算出来的。我是把7分成1 和 6,9+1=10,10+6=16,我画了个图(如图9)。
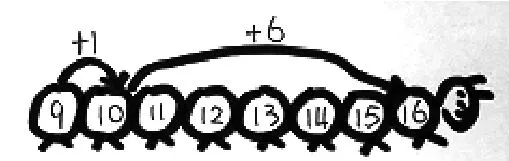
图9
生3:我的方法是从9 里面分出 3,7+3=10,10+6=16,我用画线的方法表示出来了。(如图10)

图10
生4:其实还有一种方法,一个一个数。不过大家都学习了凑十法,一个一个数的方法很多人不用了。
师:是啊,学习的过程就是这样,要学会借鉴别人好的方法来用,这样能更好地帮助我们学好数学。想一想,9+7 还可以解决生活中的哪些问题?
生1:我有7 支笔,我同学有9 支笔,我们俩一共有几支笔?
生2:我原来有9本课外书,妈妈又买来7本,我现在一共有几本课外书?
生3:我想说的是这样的例子可以举好多,说不完的。
生4:我同意生3 的意见,只要是符合条件的就行。
师:你说的符合条件是什么意思?能具体解释一下吗?
生4:只要一部分是7,一部分是9,不管是合起来,还是增加的,都是可以的。
师:能听懂生4 的意思吗?
生1:我明白了,他不是仅仅说一个例子,他说的是所有的例子。
师:真是了不起,不仅能举出生活中的例子,还能发现加法中隐藏的秘密,非常好的思路。谁还有其他问题?我们一起来交流。
生2:我解决的是“语文作业比数学作业多几颗星星”这个问题,这个问题可以用减法做,9-7=2。
师:有多少同学选择了这个问题?(学生举手)能说说为什么用减法算吗?
生1:我是这样想的(如图11),第一行代表语文作业得到的星星,第二行代表数学作业得到的星星,一个对一个,发现语文得到的星星比数学多了2颗,可以用减法来计算。

图11
生2:我想的是从语文作业得到的星星中去掉数学的那一部分,剩下的就是多的,所以用减法来算。
生3:我想提醒大家的是,不能看到多就用加法算,这道题就是用减法来算的。
师:大家思路很多,在说自己想法的时候,把计算的道理也说得很清楚。想一想,“数学作业比语文作业少几颗星星”这道题该如何算呢?
生1:9-7=2,和上面这道题的思路是一样的。
师:你能再举一个用9-7=2 完成的问题吗?
生2:盘子里有9个苹果,客人吃了7个苹果,还剩下几个苹果?
生3:我的同桌有 9本课外书,我有7本,我再有几本就和他一样多了?
师:能明白生3 的问题吗?
生4:其实也是9和7在进行比较,7本比9本少两本,所以就是 9-7=2。
师:很好地解释了他的想法。我们现在比赛一下,一组写的数是16 的加法算式,一组写的数是2 的减法算式,看看你们有什么发现。
(学生独立完成后,小组进行交流,教师巡视并进行指导)
组1:我们小组写了5个算式(如图 12),我们是以 7+9=16 为例,按照规律写的,加号前面的数多1,加号后面的数少1,结果是不变的。你们同意我们的意见吗?
(其他学生点头表示同意)
组2:我们写的是减法算式(如图 13),我们写了 4个算式,减号前面和减号后面的数要同时少1 才行。我们又实验了一下,同时减去2 也行,比如不写 8-6=2,直接写 7-5=2。
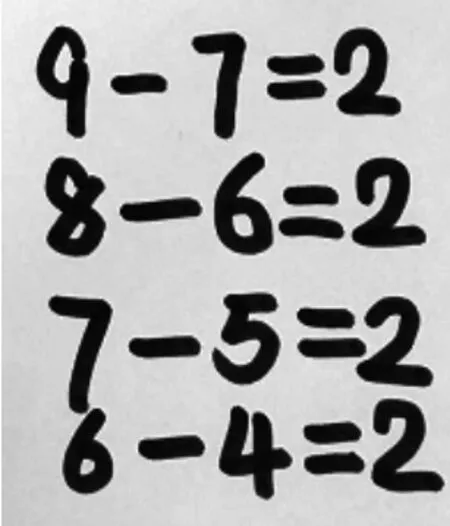
图12
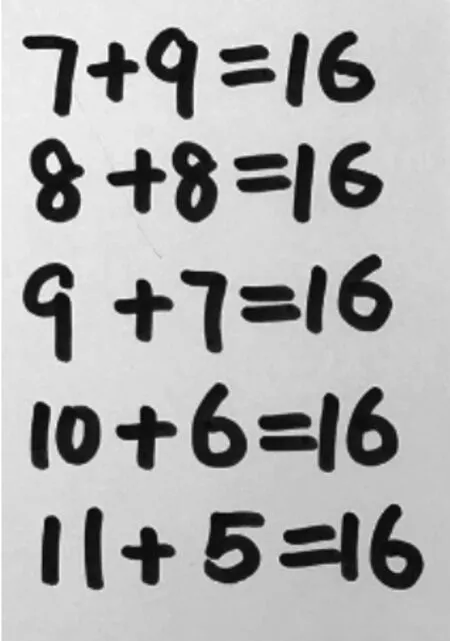
图13
师:我有一个问题想问问你们,你们怎么就写了4个算式?为什么不多写一些呢?
生:这样的算式是写不完的,只要结果是2 的减法算式都是可以的。
生:这和刚才 7+9=16 的问题是一样的,也是写不完的。
师:非常好,我们一起来回顾一下。从语文作业和数学作业得到的星星这个问题出发,我们复习了什么?
生1:我们复习了怎样列式解答问题。
生2:我们复习了 9+7=16是怎么算出来的。
生3:我们还可以根据规律写出很多得数是2 的减法算式。
师:真是不简单,我们根据一个问题,复习了这学期我们学习的加法和减法问题,课后我们可以试着用自己的方法整理一下,然后在班级里进行交流。
我们从一个问题情境出发,引领学生提出问题、解决问题、交流算法、发现算式中隐藏着的秘密,学生经历了提出问题、解决问题的过程。这一过程,看似简单,实则不易,需要学生把之前学习的内容融会贯通,才能更好地建立加、减法的意义,沟通算法之间的联系,建构知识之间的框架,这对提升学生的思维能力非常重要。
这一尝试,让我们更加坚定信念,教师要用开放的心态来看待学生的学习,关键时刻要学会放手,把学生推向前台,鼓励学生自主地进行复习,经历对所学知识及思想方法进行梳理的过程,学会反思,理解相关知识之间的区别与联系,逐步养成整理知识的良好习惯。

