一个常见平面几何题的拓展与应用*

● ●

(杭州市基础教育研究室,浙江 杭州 310003) (青春中学，浙江 杭州 310006)

“杭州市初中数学青年教师核心组”QQ群，从2018年1月3日开始在每周三和周日定时举行网络在线解题研究讨论，40余位成员轮流主持．1月3日讨论的是一道大家非常熟悉的平面几何问题，历时3小时的讨论，大家给出原题的多种不同解法以及多角度的推广，追本溯源地发现问题背后的本质，并给出向量意义下的进一步推广，以及发现了部分结论与常见问题的联系．讨论结束后大家一致认为收获满满，笔者将讨论的结果整理出来与广大初中数学教师分享．

1 原题呈现

当我们遇到熟悉的数学问题时，往往会受思维定势的影响，用自己熟悉的方法快速解决问题．殊不知，这时我们已经失去了对这个问题做进一步研究的机会．有时，对于这样的问题，重新回味一下，静下心来细细思考，会有新的收获．

原题呈现点P是矩形ABCD内一点，若AP=3，DP=2，CP=5,求BP的长．

解法1如图1，过点P作EF∥AB，分别交AD，BC于点E，F．设AE=a，DE=b，EP=c，FP=d，易证

a2+c2=9，

(1)

b2+c2=4,

(2)

b2+d2=25,

(3)

式(1)+式(3)-式(2)，得

a2+d2=30，

即

BP2=30.

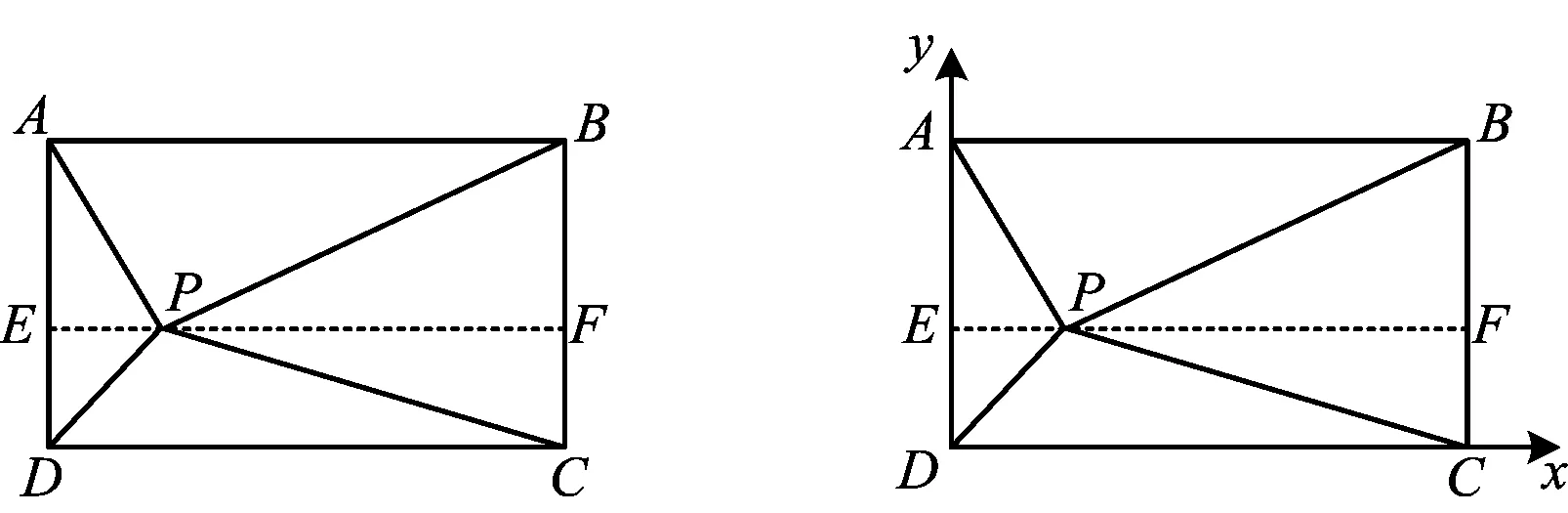
图1 图2

解法2如图2，以点D为坐标原点、分别以DC，DA所在的直线为x轴和y轴建立直角坐标系．设DA=a，DC=b，则A(0，a)，B(b，a)，C(b，0)，P(x，y)，从而

与解法1类似可得

(x-a)2+(y-b)2=30,

两种解法的共同点是：线段BP的长并不依赖矩形的形状，与矩形的边长也不构成直接相关，这引发了大家的关注和热烈讨论．以下是笔者根据讨论的内容整理而成的，为呈现一定的研究逻辑，在问题呈现的顺序上做了一定的调整．

2 相关研究

为了对原题作深入研究，给出以下4个命题，其中命题1是命题2的特例，命题3是命题2的逆命题，命题4即原题的推广．

命题1三角形相邻两边的平方差等于这两边在第三边上的射影的平方差．

如图3，在△ABC中，AD⊥BC于点D，则

AB2-AC2=BD2-DC2.

显然，根据勾股定理可得

AD2=AB2-BD2，AD2=AC2-DC2，

从而

AB2-BD2=AC2-DC2，

移项整理得AB2-AC2=BD2-DC2,

故命题1成立．

图3 图4

命题2对角线互相垂直的四边形的对边的平方和相等．

如图4，若四边形ABCD的对角线AC⊥BD，则

AB2+CD2=BC2+AD2．

显然，根据命题1可得

AB2-AD2=BE2-ED2，

BC2-CD2=BE2-ED2，

从而

AB2-AD2=BC2-CD2，

移项即得

AB2+CD2=BC2+AD2,

故命题2成立．

命题2的逆命题(命题3)是否成立呢？

命题3对边平方和相等的四边形的对角线互相垂直．

如图4，设四边形ABCD的对角线AC，BD相交于点E，若AB2+CD2=BC2+AD2，则AC⊥BD．

证明因为

AB2+CD2-BC2-AD2=

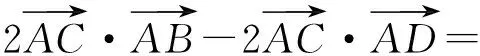
又

AB2+CD2=BC2+AD2，

所以

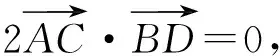
从而

AC⊥BD,

故命题3成立．

进一步研究表明，原题可推广得更一般的结论：

命题4(原题推广)若点P是矩形ABCD内一点，则PA2+PC2=PB2+PD2．

证法1如图5，过点P作EF∥AB交AD，BC于点E,F,根据命题1得

PA2-PD2=AE2-ED2=BF2-CF2=

(BF2+FP2)-(CF2+FP2)=

PB2-PC2．

移项即得PA2+PC2=PB2+PD2．

图5 图6

证法2(通过构造，进行证明)如图6，过点P作线段GH，EF分别垂直于矩形的对边，则GH⊥EF．

联结EG，GF，FH，HE，则四边形EGFH为对角线互相垂直的四边形，根据命题2，得

EG2+FH2=EH2+GF2.

又因为4个小矩形的对角线相等，即

EG=PA，GF=PB，FH=PC，EH=PD，

所以

PA2+PC2=PB2+PD2．

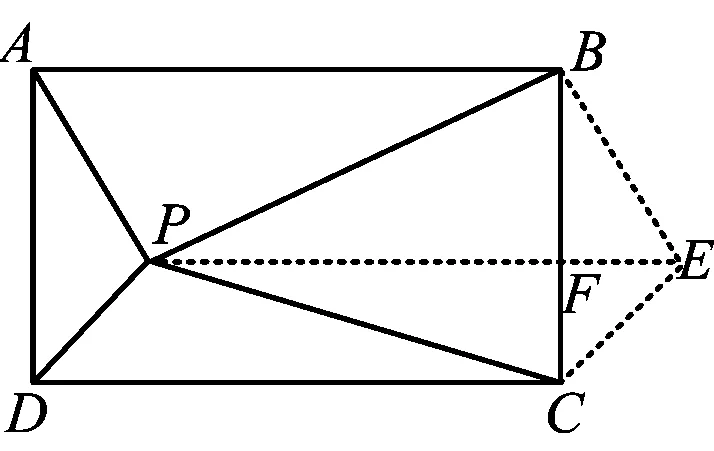
图7

证法3如图7，构造与证法2类似的证明，请读者自己完成．

这里给出的3种证法，本质上都是构造直角三角形，利用勾股定理得到线段之间的关系，体现了欧氏几何中研究定量问题的一般方法．

事实上，若点P是空间中任意一点，本题的结论仍旧成立．

3 追本溯源

命题4的逆命题成立吗？

命题5设P为四边形ABCD内一点，若PA2+PC2=PB2+PD2，则四边形ABCD是矩形．

显然，当PA，PB，PC，PD都相等时，点A，B，C，D在同一个⊙P上，满足PA2+PC2=PB2+PD2，此时四边形ABCD的形状并不不确定；当PA，PB，PC，PD不全相等时，即使点A，B，C位置固定不变，满足条件的点D也可以落在以P为圆心、PD为半径的圆上，位置也不固定，由此，四边形的形状也不一定是矩形．因此，命题5是假命题．

如果把原题改变成下面的形式出现，似乎更不容易解决了．

如图8，一组同心圆O，半径分别为2，3，5，记作⊙O1，⊙O2，⊙O3．点A，B分别在⊙O1，⊙O2上，过点B作AB的垂线，与⊙O3有两个交点，任取一个交点记作点C，分别过点A，C作AB，BC的垂线，交于点D．求证：点D必在⊙O的一个同心圆上．

图8 图9

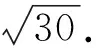
下面给出能揭示问题本源的证明：

证法4如图10，根据三角形中线公式，得

显然，AC=BD，从而

PA2+PC2=PB2+PD2．

在△APC和△BPD中，因为有了矩形这个大前提，所以AC=BD始终成立．对于符合题意的任意矩形中的点P，到矩形中心O的连线段PO是两个三角形公共的中线.由三角形中线公式，把PA2+PC2和PB2+PD2转化为矩形对角线与PO之间的关系，不变性就一目了然了．

显然，从该证明中可以看出，矩形ABCD的形状可以随着AC和BD的夹角而变化．当线段AC和BD随点O旋转时(或变成空间问题)，结论都成立．

4 再次推广

如果把结论推广到平行四边形中会得到什么结论？利用刚才的思路，这个问题就变得很清晰了．

推广1若点P为ABCD内任意一点，则

证明如图11，分别联结两条对角线，交于点O，则

证明过程中使用了向量中的常见恒等式:

4a·b=(a+b)2-(a-b)2．

5 简单应用

例1已知△ABC是等腰三角形，AB=AC，D在线段BC上，求证：AB2-AD2=BD·DC．

证明如图12，过点A作AE⊥BC于点E，则根据命题1，有

AB2-AD2=BE2-DE2=

(BE-DE)·(BE+DE)=BD·DC．

图12 图13

拓展1如图13，如果画出△ABC的外接圆⊙A，设半径为r，AD=d，则上式可改写为

BD·DC=r2-d2．

这就是相交弦定理，当D为线段BC的外分点时，则结论为

BD·DC=d2-r2．

这就是切割线定理，两者可以统一写作

BD·DC=|r2-d2|,

其中点D为线段BC的一个分点．

例2如图14，在等腰Rt△ABC中，AB=AC，∠BAC=90°，求证：BD2+DC2=2AD2．

本题证明方法很多，这里利用命题2给出证明．

证明把等腰Rt△ABC补成为一个正方形ABEC，则AD=ED，根据命题2，有

DA2+DE2=BD2+DC2,

从而

BD2+DC2=2AD2．

图14 图15

例3(三角形中线公式的证明)在△ABC中，AD为BC边上的中线，求证：

证明1)如图15，当∠BAC为直角时，

2)如图16，当∠BAC为锐角时，以BC为对角线构造矩形BECF，则由原题的一般结论得

AB2+AC2=AE2+AF2=

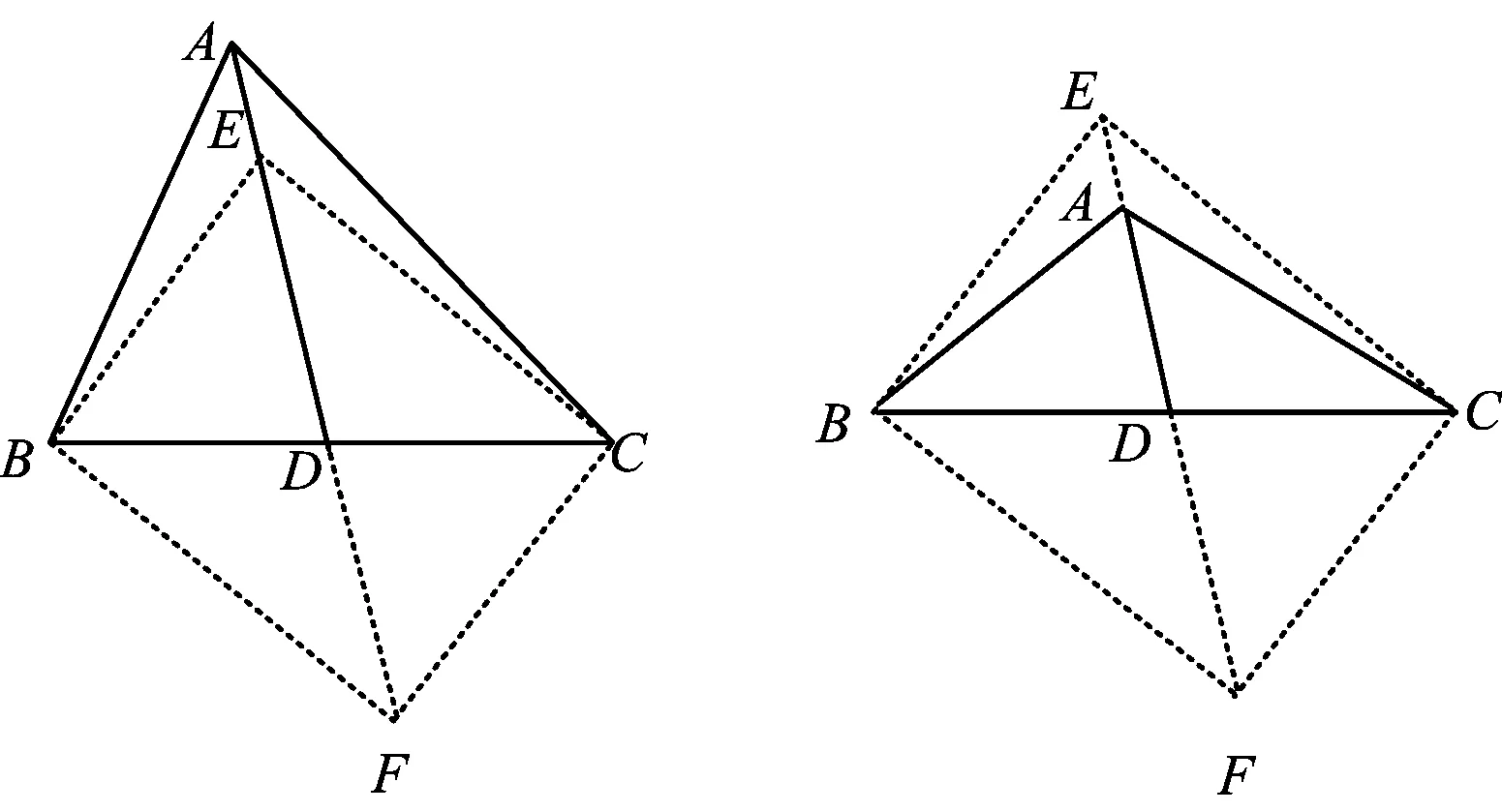
图16 图17

3)如图17，当∠BAC为钝角时，以BC为对角线构造矩形，由命题4得

AB2+AC2=AE2+AF2=

由此不难推导出三角形的中线长公式