小学数学课堂上习题分析的策略与研究

陈锋

习题研究是一种比较特别的教学研究的方式，是对某一个题目进行分析，阐述涉及的知识点，题目的价值、解决的策略、蕴含的数学思想方法等。研究习题可以从：分析题目的内容、研究数学思想方法、做好学情分析、 研究策略解决、进行变式迁移、进行反思延伸等方面展开。下面我以苏教版教材《数学》“长方体和正方体”这一单元第22页的思考题具体说明。

分析题目的内容

说题目的内容，顾名思义就是说清楚题目的结构，题目的含义，应该和学生们分析清楚题目中的已知和未知条件，题目当中可能用到的公式定理等等，甚至还可以说说此题的设计意图。以本题为例，我们分析题目是苏教版《数学》“长方体和正方体” 这一单元第22页的思考题。通过读题分析，可以知道这一题所蕴含的信息和知识点。

长方体和正方体的特征的认识，知道了长方体和正方体的各个特征，而且也知道了比较特殊的长方体（有两个相对的面是正方形）

会计算长方体和正方体的表面积的计算方法和三年级时已经学习过的长方形和正方形的计算方法。

通过观察图形找到图中变化的部分，运用所学的内容求出解决问题所需要的条件。增强学生分析问题解决问题的能力，体验成功解决问题的喜悦。

研究数学思想方法

数学思想方法一般都隐含在题目中间。学生不能顺利解决这个题目，与知识的形成过程有一定的关系。以上题为例，表面积增加的面积在哪里？变化在哪里？这里就有了变化的思想。利用观察和变换，这增加的面就是这四周的四个面积。以此看来，这题还蕴含了转化、简化的思想。

做好学情分析

学情分析就是对学生在解答题目时候可能产生的学习情况。指学生解决问题时候已经掌握的知识内容能力和思维能力，更要关注学生可能会出现错误的地方。所以，在分析题目之前，我们教师就应先把握一下学生学习的起点，关注学生已有知识经验。

从知识角度看，长方形的面积，以及根据面积和长（宽）求出宽（长）的实际问题的解决；长方体和正方体的特征、表面积和体积的计算都是学生解决此题的基础。从能力来看，四年级“解决问题的策略”单元有过长增加导致面积增加的情况，但仅限于平面图形，上升到立体图形，对知识的架构、空间几何能力的提升带来了冲突，会有一些困难，对增加的面积的理解不正确是学生常出现的问题。

研究策略解决

策略解决就是对数学习题的解答经历的过程、方法和步骤，最终得到问题的答案。通过前面对题目内容、数学思想方法的研究，对学情的分析以后，可以采用观察、猜想、画图法、推理等分析和解决问题。

上面案例中的思考题，分析的时候需要分为以下几步：

观察表面积比原来增加了56平方厘米，究竟是增加了哪些部分的面积？为什么上面的面积没有增加？

增加的四块面积在哪里？都是什么形状？它们的大小怎么样？根据这些条件我们能求出什么？

一块长方形的面积14平方厘米，长增加的2厘米在哪里？根据这两个条件能求出什么？为什么？

14÷2=7（厘米），这里的7厘米是代表那条线段？就是哪条线段？就是题目什么条件？

求原来长方体的体积你能分别找一找相关的条件吗？

进行变式迁移

变式迁移就是对数学问题进行了不同的角度不同形式的变换，彰显内涵和迁移，揭示了知识之间的联系，加深了对知识的理解和思考，并起到了举一反三的效果。

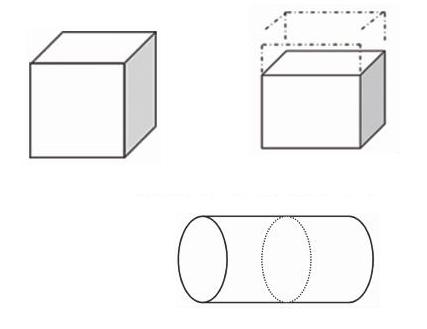
变式（1），如圖：一个正方体，如果把一条棱长缩短2厘米，就得到一个长方体，这时表面积就减少了

56平方厘米，原来正方体

的体积是多少立方厘米？

变式（2），如图：一个长方体，如果把长缩短以后，就得到一个棱长7厘米的正长方体，这时表面积就

减少了56平方厘米，那么

长缩短了多少厘米？

变式（3）：到了六年级下册学完“圆柱和圆锥”这个单元以后可以这样变式

如图：一段圆柱体木料，长16厘米，如果将它沿着底面直径截去5厘米长的一段，这时表面积就减少了31.4平方厘米，这原来跟木料的体积是多少立方厘米？

进行反思延伸

反思可以对学生的认知过程进行体会，可以不断完善，也能对此类问题进行进一步延伸，才能对相关习题有一个习题的提炼总结。只有分析了多种知识点融合的习题，通过画图、观察、猜想、推理等方法进一步体会几何图形之间的联系，同时也在解决问题的同时积累了活动经验，丰富了解决问题的方法。

综上所述，如果我们对教材上的练习题在课堂上能做好认真分析、认真研究，就能在课堂上提高效率，很多时候学生把错题一错再错与教师的讲解有一定的关系。所以，我觉得抓好习题的分析和研究，是提高教学质量的重要途径。

（江苏省苏州市吴江区坛丘小学）