破解“勾股弦公式”千古构造之谜——用代数法巧妙求出不定方程X2+Y2=Z2之通解

邹继芳

(抚顺矿业集团有限责任公司机械制造厂 113001)

用代数法巧妙求出X2+Y2=Z2不定方程的非零整数之通解

解设X=μ+A,

Y=μ+B,

Z=μ+C,

式中：μ、A、B、C都为正整数，显然C>A,C>B.

所以,X2+Y2=Z2可写成

(μ+A)2+(μ+B)2=(μ+C)2,

μ2+2μA+A2+μ2+2μB+B2=μ2+2μC+C2,

μ2+2μ(A+B-C)+A2+B2-C2=0.

设C-A=p，C-B=q，

因C、A、B为正整数，则p、q为正整数.

则Y=μ+B,

则X=μ+A,

从C-A=p，C-B=q中得

p+A=q+B,

p-B=q-A.

则Z=μ+C,

从C-B=q中得C=q+B.

即有下列关系式

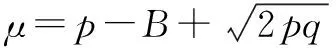
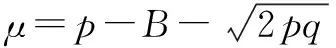
由于X、Y、Z皆为正整数，即X>0,Y>0,Z>0,

讨论:由于p>0,q>0,

q>2p；

p>2q.

很容易验证此解是X2+Y2=Z2的不为零的整数之通解.

下面来讨论此解，考察这个通解.

由于2pq必须为平方数，且2pq必须为偶数,

pq=2m2,

因p、q必须为正整数，所以说明2m2必能被q整除，也说明2m2必含有被q整除的因子.为讨论方便起见设m=a×b(a、b都是任意正整数),

则2m2=2×(a×b)2=2a2×b2,

即p×q=2m2=2a2×b2.

这样，当X、Y、Z为互质时，只有如下关系式

上式的结果比较繁琐，需要对其简化.

4γ=β2-4.

根据X=a2β，Y=a2γ，代入4γ=β2-4中,

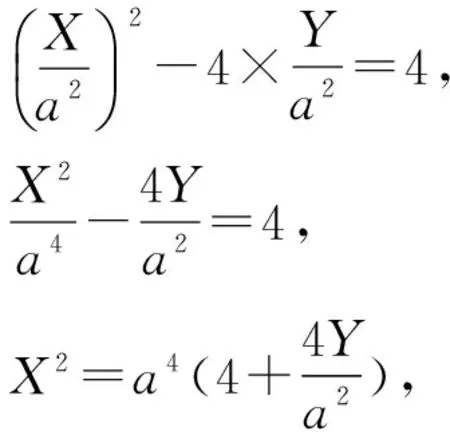
X2=4a2(a2+Y),

则X=2ad,

Y=d2-a2.

4ω=[(β-2)2+4β],

4ω=(β2-4β+4+4β).

4ω=β2+4.

根据X=a2β，Z=a2ω代入4ω=β2+4中,

4Za2-X2=4a4,

4Za2-4a4=X2,

即有如下结论：

设Z-a2=e2,则

X=2ae,

Z=e2+a2.

又因X=2ae，前式中X=2ad,所以d=e.

为统一和书写方便起见，取X=2ad.

根据上述求证结果，可得出如下结论：

不定方程X2+Y2=Z2不为零的正整数解通解为，当X、Y、Z互质时(没有公因数时),

若有公因数时，则

这样即可获取所有的整数解，即X2+Y2=Z2不定方程的非零整数之通解.

几何解析：仔细分析X2+Y2=Z2这个方程，从几何的角度来看，X、Y、Z分别代表直角三角形的三条边，三条边之间的关系为X2+Y2=Z2,这就是著名的勾股定理：在任何一个直角三角形中，两条直角边长的平方之和一定等于斜边长的平方.这个定理在中国又称为商高定理，在国外称为“毕达哥拉斯定理”.

(勾股定理几何关系)

若X、Y、Z都为正整数，则构成勾股数组

(勾股数组关系) 记为(2ad、d2-a2、d2+a2)

参考文献：

[1]张文忠.数学撷英[M].北京：科学普及出版社，1983.

[2]A·B瓦西列夫斯基.数学解题教学法[M].李光宇,王力新译.长沙：湖南科学技术出版社，1982.

[3]夏圣亭.中学数学题巧解妙法[M].上海：上海科学普及出版社，1994.