走出思维误区，培养学生思维能力

施响勇

(江苏省启东中学 226200)

一、走出“定性思维”误区，激发学生探究兴趣

许多高中生本来就对数学学习心生“畏”惧，再加上高中数学理论的枯燥乏味，导致很多学生对学科学习缺乏兴趣.然而，数学教学是一种双边活动，其特殊性要求教学需要高度的师生配合，反之则效果不佳，难以达到预期目标.因此，有效激发学生数学学习兴趣，充分调动其学习积极性，就成为高中数学教学亟待解决的问题.这就需要我们教师去认真思考、精心准备.在数学教学活动中，我们教师可以通过让学生使用数学方法进行思考、分析和解决现实生活中的实例，以此让学生感受到生活中处处包含数学，生活离不开数学，进而引导学生重视数学学科的学习.比如在学习概率内容时，针对社会上不法分子的摆地摊赌博行为，我举了如下例子：

路旁推主甲用一个口袋装了8个白球和8个黑球，摸奖者每人交一元的参与费，然后从袋中一次性去摸出5个球，如果摸到5个白球可奖励20元现金；如果摸到4个白球可奖励2元现金；如果摸到3个白球可奖励纪念品一份(价值5毛钱)；其他情况无任何奖品.问按摸1000次统计，摊主是赚钱还是赔钱？

很多人认为有利可图，就纷纷上钩，失败了也只是认为运气不好而已，却不知这里包含了数学中的概率问题.学生们对该例子也很有兴趣，他们也有人认为摊主可能面临很大的风险，于是我和学生们一起讨论了这个问题.

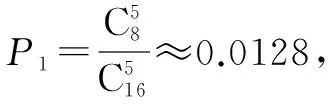
二、走出重“果”轻“因”误区，培养学生逻辑能力

公式推导是高中数学课堂教学的重要内容，涉及概念、方法以及技巧，对于学生思维、能力的培养有重要作用.然而，在实际教学中，师生都忽略了这一点，常常重“果”轻“因”，不注重公式的推导过程，止步于公式记忆，这是高中数学教学与学习普遍存在的误区.对此，就要加强重视，积极改善，一方面，注重公式的推导过程，并在公式推导过程中有意识地掺杂一些逻辑推理技巧展示给学生；另一方面，加强意识渗透，引导学生走出学习过程中重“果”轻“因”的误区.

在讲解等比数列求和公式的推导过程时，我就引导学生发现并利用等比数列的特点，巧妙地在等式两端同时乘以公比q而后作差，从而得到等比数列求和公式.这一方法也是学生解决数列求和问题中最常用的方法.

在本题的求解过程中应用的正是该方法.因此我们在教学过程中要求学生记住的并不仅仅是等比数列前n项和的公式，理解并熟知推导过程与公式变形也是要求掌握的内容.另外，在数学公式的推导教学过程中，对在解题时经常用到的步骤要着重讲解，引导学生逐步走出重“果”轻“因”的误区，促进其逻辑推理和解决问题的能力的培养.

三、走出“数形分家”误区，培养解题技巧能力

数形结合一直以来都是解决高中数学问题的有效方法之一，但很多高中生一般对“数字”比较敏感，往往会对“形”有些陌生，不善于或想不到利用数形结合的思想方法去分析解决数学问题，缺乏这方面的解题技巧.

例若关于x的方程x2+2kx+3k=0的两根都在-1和3之间，求k的取值范围

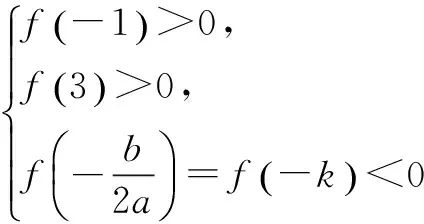
利用数形结合的方法可以很快解决该问题，可是在实际解题过程中我发现很多学生无从下手，我经过提问得知，很多学生认为这明明是“数”的问题，根本就没有利用“形”来解决问题的意识，因而无法解决此问题.像这样脑海中完全没有“形”的概念，无法灵活利用图象来分析解决问题，就是大部分高中生的通病.针对这一问题，在实际教学过程中特别是学习几何、函数内容时，要求学生熟练掌握各种函数图象，使其脑海中有由“数”想到“形”、由“形”联系到“数”的概念，并利用数形结合的思想来分析解决数学问题，最终达到培养他们解题技巧能力的目的，为以后更好的发展打下基础.

总之，激发学生学习兴趣，引导学生走出数学学习的误区，是高中数学教学长期关注的问题.在这之后，才能更好的培养学生学习数学的兴趣，掌握正确的数学学习方法，教学质量才会有提高的可能.

参考文献：

[1]向乾华.浅谈中小学数学思维训练与培养[J].读与写(教育教学刊),2017(05).

[2]郑步春.数学思维训练型课堂的建构与实践[J].江苏教育研究,2016(27).