妙用整体法 优化高中物理解题教学

徐珅爽

(福建省诏安第一中学 363500)

选择正确的解题方法是解决物理问题的关键.整体法作为一种重要的解题方法，能够将物理问题简化，大大提高解题的效率，缩短解题时间.分析以往的物理考试题目就会发现，整体法目前已经成为了考察的热点，同时它也是学生学习中的难点.本文将结合实例，探究如何在高中物理教学中运用整体法.

一、整体法的内涵

在物理学中，可以把一系列的运动过程看成一个整体，也可以把相互关联的几个对象看做一个整体.也就是说整体法是一个从个体到全局的分析思路，首先要理解物理现象的本质，然后再重新组合相互关联的多个物体，根据整体的能量变化动量变化以及所受外力的情况列出方程从而解决物理问题.由于整体法是从全局来看待问题的，因而可以忽略系统内各物体间的互相作用以及机械运动过程的一些细节，从而减少演算过程，将复杂的问题简单化也就提高了解题效率.

二、运用整体法解决物理力学问题的解题思路

运用整体法解决物理问题的思路具体地说就是：①首先要确定研究对象，这需要结合题目中的情境科学的进行选择.原则上要选与周围环境有联系，并且已知条件比较多的，在面对那些比较复杂的问题时，考虑到物体的各个部分间的相互制约，有时还需要同时分离多个对象才可以更好地够解决问题.②解决问题的关键步骤就是对受力点的受力分析.一般来说，可以先分析电场力、重力、磁场力，然后分析摩擦力、弹力这些接触力，最后再分析别的力.或者也可以采用先分析重力再分析弹力然后分析摩擦力最后分析其他力这样的顺序来分析物体的受力.采用这些分析顺序的主要目的就是尽量避免多力、少力、或者弄错力的方向.因此要叮嘱学生在受力分析的最后对研究对象的受力进行检查，养成做题的良好习惯.检查时可以依据这样的口诀：“重力肯定有，弹力看周围，摩擦看动静，方向不能错”.也就是说首先确定重力的存在，然后通过看研究对象和接触面间有没有挤压和弹性形变来对弹力和摩擦力这样的接触力进行判断，通过观察接触面与物体间有无相对滑动和是否粗糙来对动摩擦力进行判断.最后可以用“假设法”对有无静摩擦力进行判断.假设不存在静摩擦力时，如果物体的运动状态与实际情况相比不发生改变则说明假设成立无静摩擦力，若发生改变则说明静摩擦力是存在的.③最后要根据受力分析情况和研究对象的运动过程结合定律得出受力平衡的力学平衡方程，动量守恒方程或能量守恒定方程等联立求解进行得简单计算就可以得到所要求的物理量或对运动状态进行判断.

三、整体法在解决物理问题中的运用实例

1.对“研究对象”的整体法

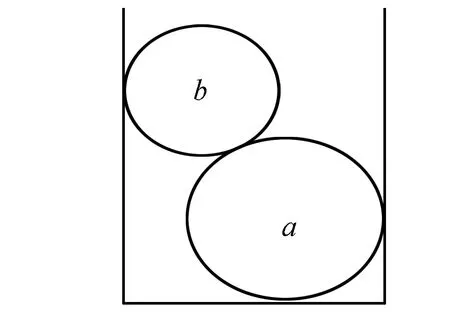
图1

例1 两个质量分别为ma和mb，刚性的小球a、b的直径分别是da和db(da>db)将a球和b球分别放入一内径为d竖直放置的圆筒内，如图1所示.设f1和f2分别为a、b两球静止时对圆筒侧面的压力的大小，F为筒底所受压力大小.已知重力加速度大小为g，如果所有的接触面的摩擦力大小忽略不计，那么则有( ).

A.F=(ma+mb)g，f1=f2

B.F=(ma+mb)g，f1≠f2

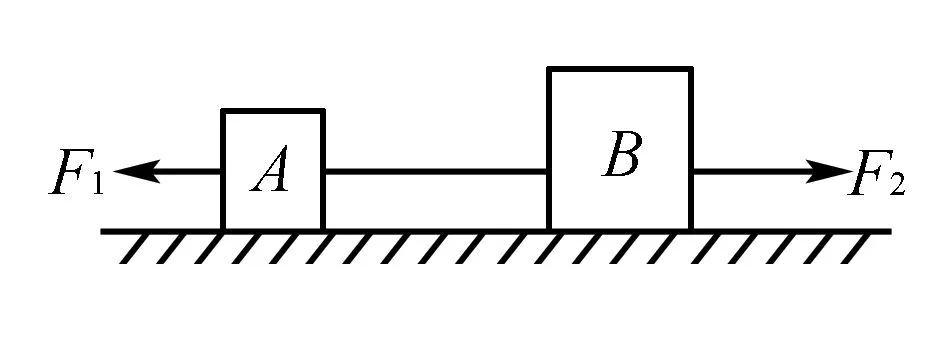
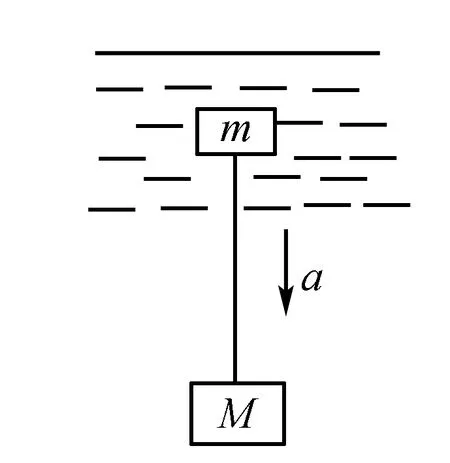
C.mag

D.mag

有相当多的典故性成语。比如“Judas kiss”，翻译为“犹大之吻”。 耶稣率领十二个门徒在各地传道，非常受欢迎，于是引起了上流社会犹太教的嫉妒，所以他们想要暗杀耶稣。耶稣的门徒为了30个银币背叛了耶稣。他亲吻耶稣来作为暗号。 “笑里藏刀 ”.因此，“犹大之吻”意味着虚伪和不安，以及可耻的叛卖行为，也可翻译为“笑里藏刀 ”。 例如，“His action to his country proved to be a Judas kiss”翻译为“他的行为是背叛祖国的行为”。

解析把球a、球b球看成是一个整体，对整体受力分析得到如图所示,在静止状态下有FN=(ma+mb)g，f1=f2,由牛顿第三定律可知：F1=f1，F2=f2，FN=F,所以有：F=(ma+mb)g，f1=f2.

故此题应该选A.

图2

例2 如图2所示，在水平光滑平面上放置物体A和物体B.其中，mA=1kg，mB=2kg，将两物体用没有弹性的一根细线相连，其中细线的质量可以忽略不计，A、B物体，各受到水平向左大小为10N的拉力F1和水平向

右大小为40N的拉力F2的作用.求A、B物体间的细线所受到的拉力的大小？

巧解因为细线是没有弹性的，因此物体A和B的加速度α相同，其大小是a=F2-F1/mA+mB=40-10/1+2=10m/s2分析A物体可知：它同时受到细线向右拉力F和F1的作用，则F-F1=mAa，即F=F1+mAa=10+1×10=20N.

综上可得：F=20N.

即答案是：细线所受拉力为20N.

2.对于“运动过程”的整体法

例3 一物体在大小为8N的水平拉力F的作用下，由静止开始沿水平方向右运动，如图3所示.物体与水平面间的动摩擦因数μ为0.2，若F经过作用时间t1=6s后撤去，又经t2=2s后与垂直墙面相撞，若物体与墙壁作用了t3=0.1s的时间，之后以v=6m/s的速度朝相反的方向弹出，那么，求墙壁对物体的平均作用力FN重力加速度为10m/s2.

图3

3.对“研究对象和运动过程”的整体法

图4

例4 从上到下依次为质量为m的木块和一块质量为M的铁块，由一根细绳连接.将其一起浸入水中，则其从静止然后以α的加速度加速下沉，细绳在时间过去t1时断开，铁块和木块继续下沉了t2以后木块不便再下沉，求这时的铁块的速度V是多少？如图4所示.

巧解铁块与木块以加速度α一起沉没，经过t1以后细绳断裂，则两者的速度相同．然后铁块加速，木则块减速．首先将木块和铁块看做是一个整体，我们根据运动情况、受力情况以及两者的关系可以进行分析.他们所受的外力应恒为总的重力和浮力之和，运动了t1之后，合力没有因绳断改变．系统从开始运动到木块停止的过程中所受的冲量为(m+M)α(t1+t2).总的动量增加了MV.根据动量定理，得：

(m+M)α(t1+t2)=MV．

所以这样考虑，就可以更为简便的得出结果了.

整体法作为一种解决物理综合大题的有效的解题方法在中学物理教学中发挥着至关重要的作用，因此应在日常教学中系统科学的应用整体法，为学生提供一种简洁有效的思维方法，从而提高学生解决物理问题的能力以及能够从更为宏观的角度看问题的素养！

参考文献：

[1]曹国星.整体法和隔离法在高中物理教学中的应用研究[D].贵阳：贵州师范大学,2015.

[2]张艳平.整体法在高中物理解题中的应用[J].考试:教研,2011(01):105-105.