关于最大公因数的一个性质及证明

赵云平

（临沧师范高等专科学校 数理系,云南 临沧 677099）

关于最大公因数的一个性质及证明

赵云平

（临沧师范高等专科学校 数理系,云南 临沧 677099）

最大公因数也称最大公约数，是两个或多个整数共有约数中最大的一个。本文主要讨论两个整数的最大公因数的性质，并给出具体的证明。

最大公因数；辗转相除法；整除；性质

1 预备知识

在数论里，最大公因数是一个非常重要的概念。最大公因数满足两条，一是公因数，二是最大。这个公因数到底存不存在呢？实际上这个公因数的存在性是比较容易判断的，因为1是任何整数的约数，所以公因数肯定是存在的，至少也有个1。那最大会不会存在呢？比如两个整数都取成0，而0可以被任何非零整数整除，所以它的公约数是任何的整数，要找最大，就找不到了。如果不全为0的话，有这样明显的结论，若a1，a2…，an不全为0，则它们的最大公因数是存在的。存在的话，关于最大公因数还有哪些重要的结论，这是本文研究的出发点。首先来回顾一下最大公因数的概念［1-5］。

定义1：若a1，a2…，an是n（n≥2）个整数，整数d是所有ai的因数，称d是a1，a2…，an的公因数。整数a1，a2…，an的公因数中最大的一个，称为 a1，a2…，an的最大公因数，记作a1，a2…，an。

定理1：若a1，a2…，an是任意个不全为零的整数，则

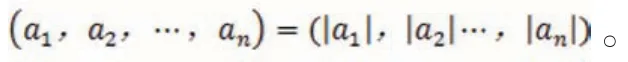
也就是说将来在讨论最大公因数的时候，如果里边的数有负号，可以把负号去掉。

定理3：设a，b，c是任意三个不全为0的整数，且a=bq+c，其中q是非零整数，则(a，b)=(b，c)。

证明：设（a，b）=d1，（b，c）=d2，证明这两个公因数相等即要证明d1=d2，只要证明d1≤d2，d2≤d1同时成立，那么这两个公因数相等。

i）证d1≤d2，由已知（a，b）=d1，则d1a，d1b，又c=a-bq，则d1也能整除a，b的线性组合，所以d1c。由d1b，d1c，推出d1是b，c的公因数，又因为（b，c）=d2，所以d1≤d2。

ii）证d2≤d1，由已知（b，c）=d2，则d2b，d2c，又a=bq+c，则d2也能整除b，c的线性组合，所以d2a。由d2a，d2b，推出d2是a，b的公因数，又因为（a，b）=d1，所以d2≤d1。

综上所述，d1=d2，即(a，b)=（b，c）。

定理3的好处就是在求最大公因数的时候，可以将大数化为小数来求，如此反复进行下去就是所谓的辗转相除法。

2 最大公因数的性质

下面针对最大公因数的一个性质，给出详细及不同证明方法。性质[2]：设a,b是任意两个不全为零的整数，则

（i）若m是任一正整数，则(am,bm)=(a,b)m。

教科书中对于证明过程已经写得很好了，但是不够明确。

证明：当a,b有一个为零时，由定理2，定理显然成立，下面设a,b都不为零

（i）证法（一），

由定理1，假定a,b＞0，由辗转相除法，有

由（3）（4），得c1=mc2

在求解最大公因数过程中，应用定理（i）可以简化计算。

（ii）由结论（i），

也就是说，a和b都除以最大公因数求它们的最大公因数是互质的。

由此就得到处理（a，b）=d的一个很好的办法：

如果（a,b）=d，那么a=da1，b=db1，且（a1,b1）=1。

反过来也是对的，d是a、b的公约数，若a=da1，b=db1，且（a1，b1）=1 ，那么（a，b)=d。这是处理最大公因数的一个非常有用的方法。

3 结论

本文利用辗转相除法和相互整除的关系证明了两个数的最大公因数的性质（i），从而比较容易地证明了性质（ii），如果是多个数的公因数需要做进一步讨论。

注释及参考文献：

[1]陈全国，刘淼.关于最大公因数和最小公倍数的一点注记[J].牡丹江大学学报，2014（10）：140-141.

[2]闵嗣鹤，严士健.初等数论（第三版）[M].北京：高等教育出版社，2003.

[3]课程教材研究所.初等数论[M].北京：人民教育出版社，2006.

[4]胡典顺,徐汉文.初等数论[M].北京：科学出版社，2010.

[5]潘承洞,潘承彪.初等数论[M].北京：北京大学出版社，2002.

One Property of the Greatest Common Factor and Its Proof

ZHAO Yun-ping
(Department of Mathematics and Science,Lincang Teachers’College,Lincang,Yunnan 677099)

The greatest common factor is also called the highest common divisor,which is the highest one of the common divisors of two or more integers.The property of the greatest common factor of two integers will be mainly discussed with its concrete proof.

the greatest common factor;algorithm of division;divisibility;the property

O156.1

A

1673-1891（2015）02-0030-02

2015-05-03

赵云平（1982-），女，云南临沧人，硕士，讲师，研究方向:基础数学数论应用，应用数学运筹学线性规划，数值代数。