基于λ-强截集的广义模糊时间序列预测模型

田宗浩，顾国华，王 鹏，王常青

（陆军军官学院，合肥 230031）

0 引言

1993年，Song和Chissom[1-3]首次提出了基于模糊集理论的时间序列预测模型，即模糊时间序列（Fuzzy Time Series,FTS）。为了提升FTS模型的预测精度，研究者们经过二十多年对FTS的不断探索，一些新的算法和思想逐渐应用到模型中[4-6]，其相应的理论和应用不断完善。在FTS模型的预测过程中，不同因素对预测结果的影响不一样，为此引入权重因子对模型进行改进[7-9]。2005年，Yu[10]提出利用模糊逻辑关系矩阵中模糊逻辑关系出现的频率建立权重模型；2006年Cheng[11，12]引入趋势权重的概念建立模糊时间序列模型对台湾股指进行预测，并取得较好的预测效果；2012年邱望仁[13]指出传统加权模型计算出观测值对每个模糊集的隶属度后，仅考虑了最大隶属度所对应的模糊状态，并没有充分利用观测样本隶属于各个模糊状态的隶属度，这样的处理方式显然会丢失掉一些有用的信息。为此，文献[13]依据样本数据对每个模糊子集的隶属度，设定要考虑的隶属度个数，对Chen和Lee加权模型进行改进，进一步提高了模型的预测精度。

邱望仁[13]首次提出了广义模糊时间序列模型的概念，并给出了广义模糊时间序列模型的定义。不同之处在于，广义模型不仅充分考虑观测样本隶属于各个模糊集的隶属度，而且还以此建立了不同层次的模糊逻辑关系，并把要考虑的隶属度值作为预测值模型的权重，很大程度上提高了模型的可解释性和预测精度。2016年王庆林[14]建立了基于GA算法的广义模糊时间序列预测模型，并且对旅游需求进行了预测，预测结果显著提高。通过分析发现，文献[13]和文献[14]中要考虑隶属度的个数是人为主观确定的，当考虑的隶属度个数一定时，如果样本数据对模糊集的隶属度太小，那么它们的引入不仅会增加模型的复杂度，而且会降低预测精度。为此，本文结合模糊集理论中λ-强截集[15，16]的性质，依据观测值对模糊集的隶属度大小来确定要考虑的隶属度个数，改进文献[13]和文献[14]提出的广义模糊时间序列模型，并通过Alabama大学22年的入学人数对改进的模型进行验证分析。

1 基本概念

定义1[15]：假设X为一个普通的非空集合，其模糊子集A定义为A={(x，μA(x))|x∈X} ，其中μA(x)表示x对A的隶属度，μA(x)∈[0，1]，映射A(·)或者μA(·)|X→[0，1]，x↦μA(x)称为模糊集A的隶属函数。

定义2[16]：假设U(X)为X上模糊集合的全体，则A∈U(X)，对∀λ∈[0，1]，记(A)λ=Aλ={x|μA(x)≥λ}为A的λ截集，Aλˉ={x|μA(x)＞λ}为A的λ强截集，称λ为阈值或者置信水平。

定义3[13]：实数集R的一个子集Y(t)，(t=1，2，…)表示论域，在论域Y(t)上定义n个模糊集Ai(i=1，2，…，n)，fAi(t)是定义在模糊集Ai上的隶属函数，F(t)是fAi(t)的集合，则F(t)就定义为论域Y(t)上的一个模糊时间序列。

定义4[13]：假设状态F(t+1)由F(t)转移得到，则F(t+1)的一阶模型可以表示为F(t+1)=F(t)◦R(t，t+1)，其中R(t，t+1)表示模糊逻辑关系矩阵，模糊逻辑关系矩阵的建立可以参考文献[10-13]。

定义 5[14]：设是时间序列Y(t)上t时刻的观测值xt对应的模糊状态，F(t+1)=是时间序列Y(t)上t+1时刻的观测值xt+1对应的模糊状态，fAi(xt)和fAj(xt+1)分别为观测值xt和xt+1对模糊集Ai和Aj的隶属度，则F(t+1)和F(t)之间的模糊关系可以表示为称之为广义的模糊逻辑关系，其中和分别称为广义模糊逻辑关系的前件和后件。

2 基于λ强截集的广义模糊逻辑关系

传统FTS预测模型在利用t时刻的样本数据对下一时刻的值进行预测时，仅仅利用了t时刻的样本数据对各个模糊集隶属度中最大的模糊状态，而将其他隶属度所对应的模糊状态忽略掉，这样的处理方式显然会丢失掉一些有用的信息。而文献[13]和文献[14]建立的广义模糊时间序列模型中，模糊逻辑关系依据要考虑的隶属度个数而定。通过对文献[13]和文献[14]中广义模糊逻辑关系的分析，要考虑隶属度的个数K由人为主观的确定，对于这样的广义模糊关系而言，当K=1时，广义的模糊时间序列就退化成只考虑最大隶属度的模糊时间序列；当K的值过大时，不仅会增加模型的计算复杂度，而且也会引入一些多余的信息，反而得不到理想的预测结果。虽然邱望仁和王庆林也为模型做了相应的简化处理，只考虑了模糊逻辑关系FLR( )

l，1，1≤l≤K，即t时刻第l位隶属度对应的模糊状态与t+1时刻最大隶属度对应模糊状态之间的关系，但是当样本数据第l位的隶属度很小时，其对应的模糊状态对下一时刻的影响也会微乎其微，过多考虑反而会增加模型的复杂度、降低预测精度。为此，本文结合模糊集理论中λ强截集的性质，通过设定合理的阈值λ，筛选出对预测结果影响比较大的模糊状态，增强了广义模型的可解释性。

首先设定一个合理的阈值λ，假设t时刻的样本数据对每个模糊集的隶属度为 (fA1(xt)，fA2(xt)，…，fAn(xt))，依据公式（1）以及定义2强截集的性质对其进行预处理，确定要考虑的模糊状态：

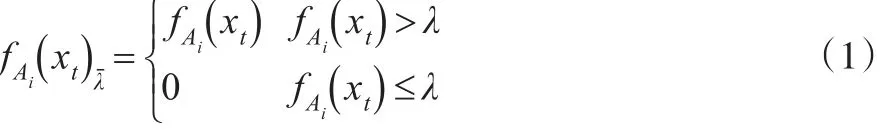
由此得到t时刻要考虑的模糊状态个数Kt以及相应模糊状态对应的隶属度，将其按从大到小的顺序排列为，其中是排在l位的隶属度，其对应的模糊状态为Ati，由此得到t时刻需要考虑的模糊状态；同理，t+1时刻要考虑模糊状态的个数为Kt+1，其中是排在k位的隶属度，其对应的模糊状态为则将称为t时刻到t+1时刻第l层模糊状态与第k层模糊状态之间的模糊逻辑关系，记为FLR(l，k)，其中1≤l≤Kt，1≤k≤Kt+1，则这样的广义模糊逻辑关系组包含Kt×Kt+1个普通的模糊逻辑关系。

3 基于λ强截集的广义模糊时间序列模型

为了增强广义模糊时间序列模型的可解释性和提高模型的预测精度，本文以Chen和Lee模型的基本框架为基础，利用λ强截集的性质以及广义模糊逻辑关系的相关运算，合理地选取要考虑的模糊状态，建立基于λ强截集的广义模糊时间序列模型。

第一步：论域划分及数据模糊化。

采用传统模型等分论域划分方法对样本数据进行划分，以便简化本文建立模型的计算复杂度以及满足下文对比分析的需要。假设U=[xmin-δ1，xmax+δ2] ，将论域U划分成n个模糊子集U=(u1，u2，…，un)，其中，d1=xmin-δ1，xmin和xmax分别为观测样本数据中的最小值和最大值，δ1和δ2分别为两个合适的正数。

用式（2）计算观测样本数据对每个模糊子集的隶属度，从而确定样本数据对应的模糊概念。

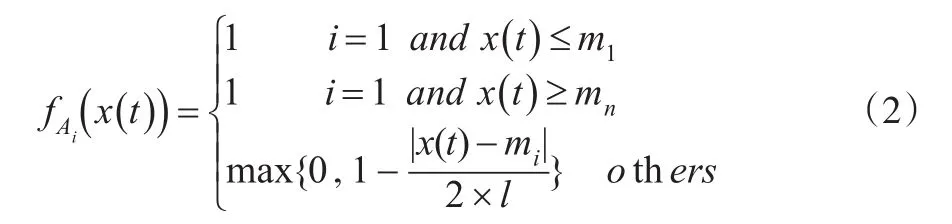
其中，x(t)为t时刻的观测样本数据，mi为第i个模糊子区间的中间值，l为等分论域区间间隔长度。

第二步：确定要考虑的隶属度个数，并做归一化处理。

针对第一步中数据模糊化的结果，计算得到样本数据对每个模糊子集的隶属度向量(fA1(x(t))，fA2(x(t))，…，fAn(x(t)))，设定合理的阈值λ，依据公式（1）确定t时刻要考虑的隶属度个数Kt以及其对应的模糊概念，引入公式（3）对预处理后的隶属度向量标准化，为预测确定权重：

其中，n为划分模糊概念个数，x(t)为t时刻观测样本数据。

第三步：依据训练数据的先后建立模糊逻辑关系及关系矩阵。

这一步是本方法的关键所在，根据第二步可以分别确定出t时刻要考虑的隶属度个数Kt以及其对应的模糊概念Ait；同理可以得出t+1时刻需要考虑的隶属度个数Kt+1和对应的模糊概念，由此可以得到t和t+1时刻之间Kt×Kt+1个模糊逻辑关系。根据各个时刻所确定的隶属度个数Kt，t=1，2，…，利用公式（4）确定需要建立模糊逻辑关系矩阵的个数K：

为了简化模型的计算复杂度，本文只考虑模糊逻辑关系FLR(k，1)，1≤k≤Kt，即，假设(x(t))和(x(t+1) )分别为t和t+1时刻观测值x(t)和x(t+1)对模糊子集的隶属度向量中第k大的隶属度和第一大隶属度值，其对应的模糊子集分别为和，则为对应的第k层模糊逻辑关系，按照时间先后顺序建立第k层模糊逻辑关系集合。依据得到的模糊逻辑关系集合，可以得到K个模糊逻辑关系矩阵Rk，1≤k≤K，相应的关系矩阵建立方法和Chen、Lee模型相同。

第四步：建立预测模型。

依据t时刻要考虑的最大隶属度的个数Kt以及第k大隶属度对应的模糊状态Ai，并利用第三步建立的关系矩阵Rk，依次得到第k个最大隶属度对应的预测值Fvalk(t+1)：

这样就可以得到Kt个预测值，利用公式（3）归一化后的隶属度向量作为第k个最大隶属度对应的预测值Fvalk(t+1)的权重值，为此可以得到t+1时刻的预测值为：

第五步：预测效果评估。

为了评价本文建立的λ强截集的广义FTS模型的优劣，通常采用误差形式来分析预测结果。但是单一的误差分析形式可能由于误差算法自身所存在的缺陷导致评价结果不可靠或者不正确，为此，本文采用均方误差MSE和泰尔不等系数TIC来衡量模型的预测精度[17]。

其中，x(t)为样本数据，Fval(t)为其对应的预测值。

4 实例验证

利用Alabama大学22年的入学人数为实验数据对本文模型的可行性进行验证（数据来源于文献[13]）。首先设置合理的阈值λ，然后利用文中广义模糊逻辑关系建立的方法得到广义模糊逻辑关系矩阵，最后将本文提出的方法与传统的加权模型和广义模型的预测结果进行对比分析，评价本文所建立模型的优劣。

为了对比分析的需要，依旧采用Song提出的7等分论域划分方法，对应的语义解释为：“极少”、“很少”、“少”、“正常”、“多”、“很多”和“较多”，利用式（2）对观测样本数据模糊化，各个样本隶属于每个模糊子集的隶属度见表1。

表1 样本数据模糊化隶属度

设定合理的阈值λ，依据表1实验数据对每个模糊子集的隶属度获得每个时刻需要考虑的模糊状态。为了简化计算过程和说明问题的方便，本文考虑λ分别为0，0.35，0.5，0.7四种情况下各个时刻对应的模糊状态并且按照隶属度大小排列（见表2）：

表2 λ分别为0，0.35，0.5，0.7时各个时刻需要考虑的模糊状态

以λ=0.35为例，可以确定需要建立3层模糊关系，依据上文建立广义的模糊逻辑关系的步骤可得：

（1）第1层模糊关系

（2）第2层模糊关系

（3）第3层模糊关系

依据上述模糊关系，分别应用Chen和Lee两种模糊逻辑关系矩阵的建立方法，得到本文建立广义模型的模糊关系矩阵为：

（1）Chen模糊关系矩阵

（2）Lee模糊关系矩阵

结合样本数据隶属于各个模糊子集的隶属度（表1）以及设置的阈值λ，利用式（1）和式（4）对隶属度表进行预处理和归一化，并将归一化后样本数据的隶属度向量作为预测值的权重。参照Chen和Lee建立模型的预测规则，分别求出t时刻第k大隶属度对应模糊子集对下一时刻的预测值Fvalk(t+1)，然后采用式（7）求解出模型的最终预测结果。下面以Chen建立的模型为例求解预测值，例如：λ=0.35，1972年的观测样本数据对各个模糊子集的隶属度向量为 (0.9685，0.5315，0.0315，0，0，0，0)，观测值对应的模糊集为A1和A2，归一化后的隶属度向量为(0.6457，0.3543，0，0，0，0，0)，最大隶属度对应的模糊子集为A1，其预测主要用到的模糊关系对应于RC(1)的第一行，此时的预测值Fval1(1973)为14000；次大隶属度对应的模糊子集为A2，用到的主要模糊关系为RC(2)的第二行，此时的预测值Fval2(1973)为14500，则1973年的最终预测值为0.6457×14000+0.3543×14500=14177。类似的可以得到其他各年的预测结果，Lee模型的预测过程也与此类似，表3为邱望仁提出的加权模型和广义模糊时间序列模型与本文λ=0.35时广义模糊时间序列模型分别在Chen和Lee加权模型上应用的预测结果，最后两行分别为对应模型的均方误差和泰尔不等系数；表4为改进模型在考虑不同λ时的预测精度变化情况。

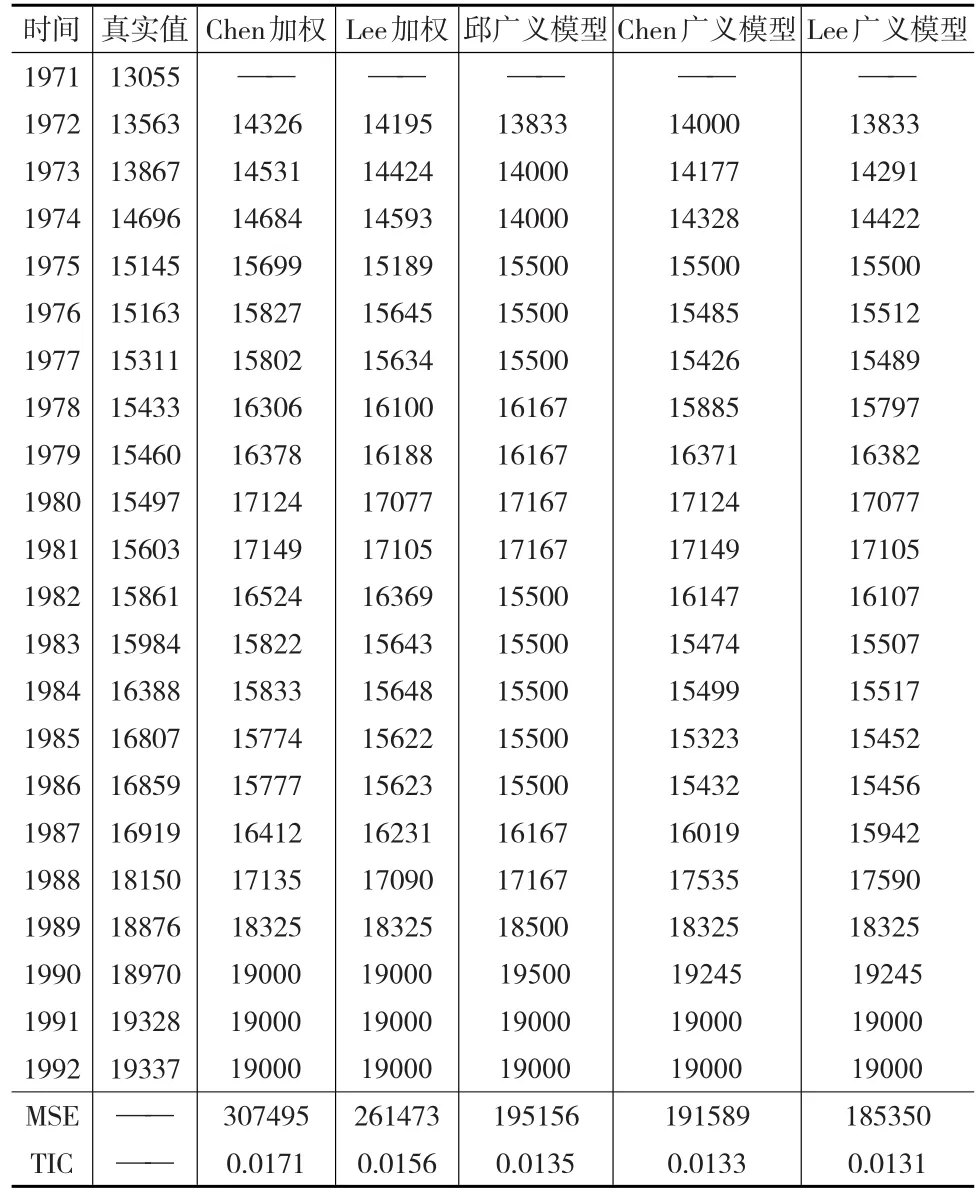
表3 λ=0.35时广义模型与其他模型的预测结果

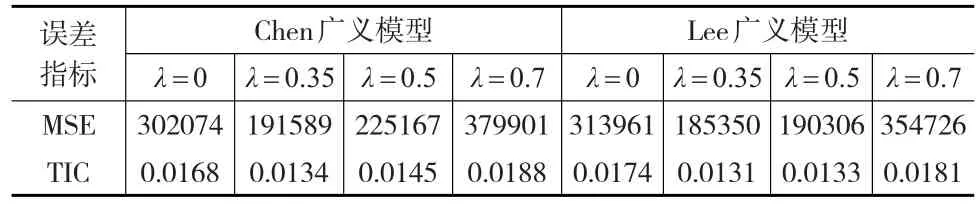
表4 λ=0，0.35，0.5，0.7情况下预测精度表

由表3可以分析出本文建立的基于λ截集的广义模糊时间序列模型在λ=0.35时得到的结果的均方误差和泰尔不等系数都比对应的文献[13]中的加权模型和广义模糊时间序列模型要低，这说明了本文改进模型的可行性和可靠性；表4列出了本文改进模型在考虑不同λ时的预测精度变化情况，当λ取值很小时，广义模型考虑的隶属度个数会很多，但是有用的信息一般是有限的，过多的信息反而降低模型的预测精度；当λ取值很大时，考虑的隶属度个数会减少，为此会丢失掉一些有用的信息，模型的预测精度依旧不会很高。因此，根据样本数据的分布结构特征和实际应用的意义，合理地选取阈值λ的值对模型的预测精度至关重要。

5 结束语

本文通过分析传统的加权以及广义模糊时间序列模型的建模过程，指出传统模型对隶属度的处理以及模糊逻辑关系矩阵的建立存在缺陷，为此本文重新定义所要考虑隶属度对应的模糊关系和预测所需的模糊逻辑关系矩阵，建立基于λ强截集的广义模糊时间序列模型。利用均方误差MSE和泰尔不等系数TIC对比分析本文提出模型和传统加权模型和广义模型的预测精度以及不同λ取值情况下模型预测精度的变化情况，验证了本文建立模型的可行性和有效性。但是本文建立的模型仅仅考虑了等间隔论域划分情况，不能充分考虑数据的结构特征，为此，在非等间隔论域划分情况下本文模型的效用依旧值得深入探究，另外，阈值λ的选取也是未来研究的重点。

参考文献：

[1]Song Q,Chissom B S.Fuzzy Time Series and Its Models[J].Fuzzy Sets Syst,1993,(54).

[2]Song Q,Chissom B S.Forecasting Enrollments With Fuzzy Time Se⁃ries-Part I[J].Fuzzy Sets Syst,1993,(54).

[3]Song Q,Chissom B S.Forecasting Enrollments With Fuzzy Time Se⁃ries-Part II[J].Fuzzy Sets Syst,1993,(52).

[4]邱望仁,刘晓东.基于AFS拓扑和FCM的模糊聚类分析[J].模糊系统与数学,2010,22(4).

[5]张志强.基于模糊逻辑关系组的时间序列模型改进[J].应用数学学报,2015,38(4).

[6]刘齐林,曾玲,曾祥艳.基于支持向量机的区间模糊数时间序列预测[J].数学的实践与认识,2015,45(22).

[7]李学森,王本德,凌贤长,周惠成.权重趋势系数模糊优选法在供水评价中的应用[J].哈尔滨理工学院学报,2009,41(6).

[8]刘晓娟,方建安.综合权重的模糊时间序列的电力负荷预测方法[J].华东电力,2012,40(4).

[9]何晓庆,蔡娜.基于模糊自适应变权重的经济时间序列组合预测模型研究[J].理论探讨,2013,27(1).

[10]Yu H K.Weighted Fuzzy Time Series Model for TAIEX Forecasting[J].Physica A,2005,(349).

[11]Cheng C H,Chen Y S,Wu Y L.Forecasting Innovation Diffusion of products Using Trend Weighted Fuzzy Time Series Model[J].Ex⁃pert System With Applications,2009,(36).

[12]Cheng C H,Chen T L,Chiang C H.Trend-weighted Fuzzy Time Se⁃ries Model for TAIEX Forecasting[J].ICONIP,2006,(4234).

[13]邱望仁.模糊时间序列模型理论及应用研究[M].天津：天津大学出版社,2013.

[14]王庆林,杨志辉.基于GA的广义模糊时间序列建模及其在旅游需求预测中的应用[J].江西科学,2015,33(5).

[15]Zadeh L A.Fuzzy Sets[J].Information and Control,1965,8(3).

[16]刘林等.应用模糊数学[M].西安:陕西科学技术出版社,2008.

[17]周春楠,黄少滨等.基于谱聚类的高阶模糊时序自适应预测方法[J].通信学报,2016,2(37).