基于Brewer设计的不放回不等概率抽样方法

王智光，闫在在，张婷婷

（1.内蒙古医科大学附属医院 神经内科，呼和浩特 010050；2.内蒙古工业大学 理学院，呼和浩特 010051）

0 引言

不放回不等概率抽样是抽样调查中的一种重要抽样形式，在实际中被广泛应用。Horvitz和Thompson(1952)[1]给出了不放回不等概率抽样下总体总值的估计量，估计量的方差及其方差估计；如何构造和实施πPS抽样设计是一个长期公开问题。Brewer和Hanif(1983)[2]总结了50种不放回不等概率抽样方法；Zou和Feng(1995)[3]也给出了一种新的不等概率抽样方法。而在实际应用中，n=2时的πPS应用最为广泛，研究也最充分。Brewer(1963)[4],Durbin(1967)[5]提出了样本单元数为n=2时的严格不放回πPS抽样方法;Rao等(1962)[6]提出了随机划分总体为n个子总体，在每个子总体中实施大小为1的不等概率抽样设计及其理论。在上述研究成果基础上，本文探索这些方法的改进或者结合使用以获取新的具有潜在应用性且精度更高的抽样设计方法，提出一种新的近似πPS抽样设计并建立该设计相应的理论。对于一些难以得到解析表达式的结果，可以利用统计软件R作数值模拟计算相应的量，从而实现提出方法和已有一些经典方法精度比较的目的。具体地，Rao等[6]提出的方法：将总体中的单元随机地划分成n组，每组的单元数记为N1，N2，…，Nn（预先确定的），在每组中按与单元大小Zi成比例的概率抽取一个单元入样，得到固定容量为n的样本。简言之，此方法是将总体划分，然后在每个子总体中实施样本量为1的不等概率抽样。受此方法启示，众所周知，存在一些经典的样本量为2的严格的不放回不等概率抽样设计，本文拟利用此思想并结合Brewer(1963)[4]或者Durbin(1967)[5]提出的n=2时的严格不放回πPS抽样方法构建新的抽样设计。

1 经典不等概率抽样方法介绍

Rao等[6]提出一个简单而适用的方法。总体U={1，2,…，N}，Y是研究变量。Zt是总体U中抽取一个单元取到第t个单元的概率。将总体中的单元随机地分成n，每组的单元数记为N2，…，Nn，在第g组中，每个单元对应的Z值重新记为，对应的Y值重新记为Yi(

g)，i=1，2，…，Ng,Z(g)是第g组中Z值的总和。在每组中按与Zj(g),j=1，2，…，Ng,Z(g)成比例抽取一个单元，最后合成样本容量为n的样本s。记第g组中抽到的样本单元观测值yg，相应的Z值记为zg。总体总值Y的Rao-Hartley-Cochran估计量定义为：

Rao-Hartley-Cochran估计量是总体总值Y的无偏估计,具有方差：

Hajek（1964）[7]设计了一种不放回的近似严格πPS抽样方法,即泊松抽样，设计如下：对每个总体单元赋予一个入样概率πi,使得πi/Zi=ν,其中ν是一个常数。以πi为成功概率，作一次Bernoulli试验，若试验成功，则相应的单元入样，共做N次试验，实际样本容量是一个随机变量。总体总值Y的无偏估计量定义为：

具有方差：

虽然泊松抽样设计实施简单，但存在一大缺点，即样本量n是随机的。为了克服泊松抽样设计上的缺点，Hajek(1981)[8]讨论了一种固定样本量n的泊松抽样方法即条件泊松抽样，它的具体实施方法如下:以pi，i∈U(满足作为一组工作概率连续进行泊松抽样，直到出现容量正好等于预定的固定样本量n的样本，则抽样结束,否则,继续上述抽样。条件泊松抽样是基于泊松抽样得到的一种不等概率抽样设计，此设计是样本量n固定，严格不放回的，但包含概率πi与单元大小不是严格成比例的近似πPS抽样设计。之后，基于泊松抽样、条件泊松抽样的不放回不等概率抽样设计有大量的研究，如Grafstrom(2009)[9]提出的Repeated Poisson抽样和Laitila等（2011）[10]提出的一种二相πPS抽样设计。条件泊松抽样的一阶包含概率计算有相应的递推公式，即：

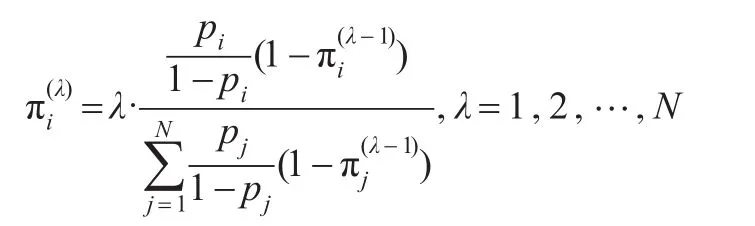
二阶包含概率的递推公式为：

2 抽样方法的提出

令总体U={1，2，…，N},y是研究变量。Zt是总体U中抽取一个单元取到第t个单元的概率,例如按与单元大小Xt成正比抽样预定的样本容量n,提出的抽样方法由以下两步组成:

(1)将总体中的单元随机地分成m=n/2（若i=1，2，…，Ng为偶数）组或者m=(n+1)/2（若n为奇数）组,每组的单元数记为N1，N2，…，Nm,其中N1+N2+ … +Nt=N。

（2）如果n为偶数,在每组中按照Brewer方法或者Durbin方法抽取两个单元,即可得到容量为n的样本s；如果n为奇数,同样在前面m-1个组中按照Brewer方法或者Durbin方法抽取两个单元,在最后一个组中按单元大小成比例抽取一个单元,即可得到容量为n的样本s。

对于上面提出的抽样设计,构造总体总值估计量,并计算其均值、方差及其方差估计,给出解析表达式。如解析表达式不易得到或过于复杂,可以通过数值模拟来计算相应的量,进而比较本文提出的方法和Rao-Hartley-Cochran方法的精度。

2.1 n为偶数的情形

假定将总体随机划分为m(=n/2)组：记为G1，G2，…，Gm。在第g组Gg中,每个单元对应的Z值在此重新记为,对应的Y值重新记为将每组中的Z值归一化记为

利用Brewer方法,在第g组Gg中两个样本单元的抽取方法是：

提出的抽样方案是容易实施的,但是抽样机制相对复杂,可以想到估计量（6）的理论分析是困难的。下面从理论和数值上评价提出的估计（6）。本文记E1和V1分别表示随机分组的数学期望和方差；E2和V2分别表示在固定分组条件下抽样设计的数学期望和方差。

可以证明估计量是总体总值Y的无偏估计。

定理1：在提出抽样设计下,E()=Y。

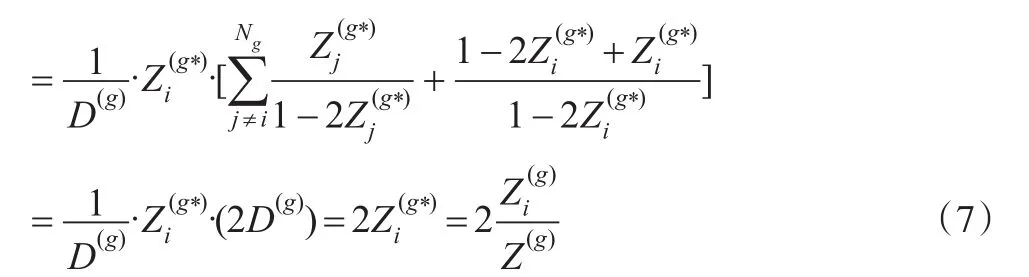
由式(1)和式(3)可以得到：

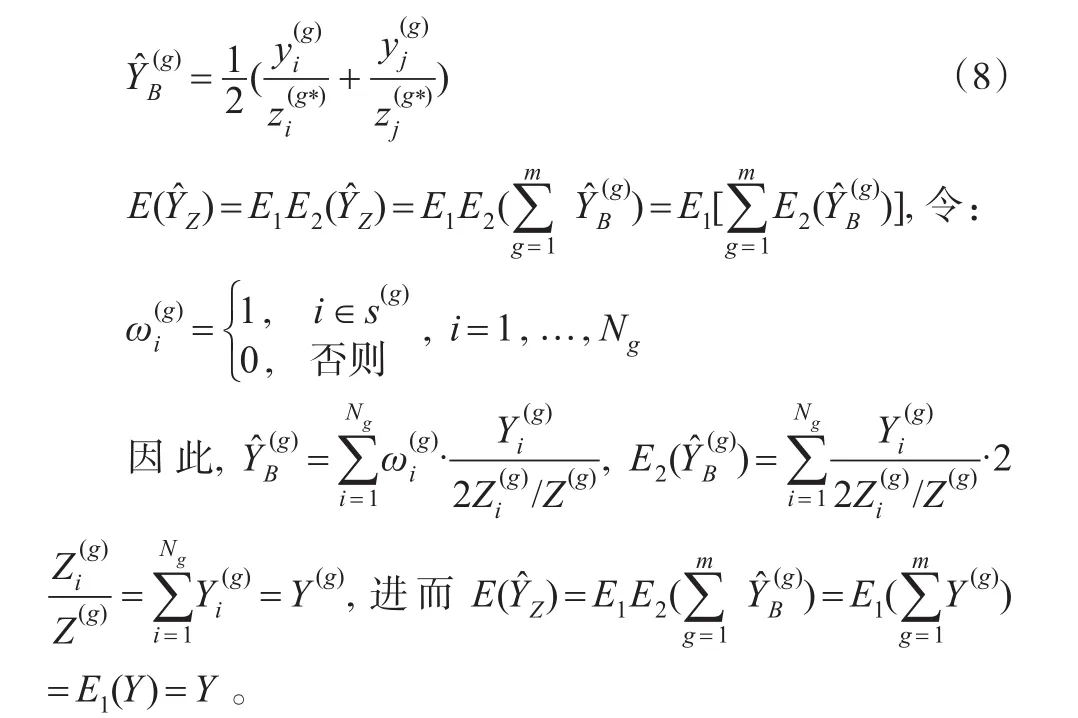
上述证明得到估计量是总体总值Y的无偏估计。下面给出估计量的方差表达式。

定理2：在提出抽样设计下：

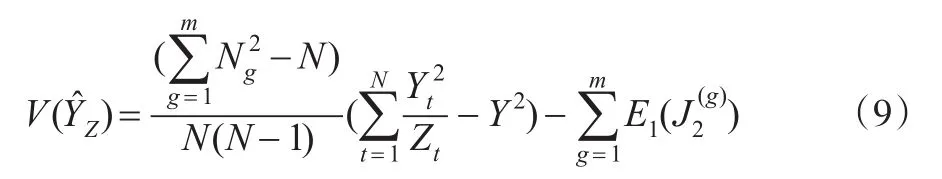
证明：

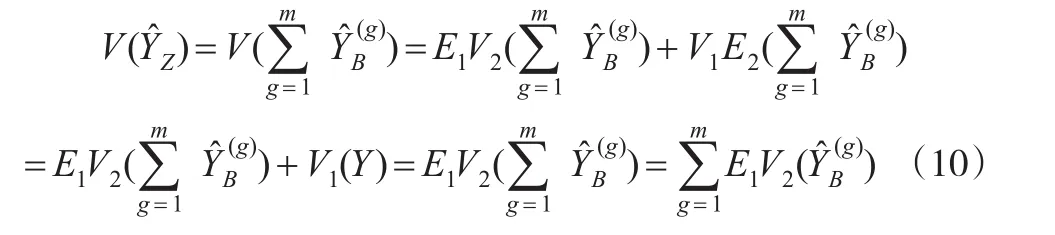
根据Horvitz-Thompson估计量的性质，有：

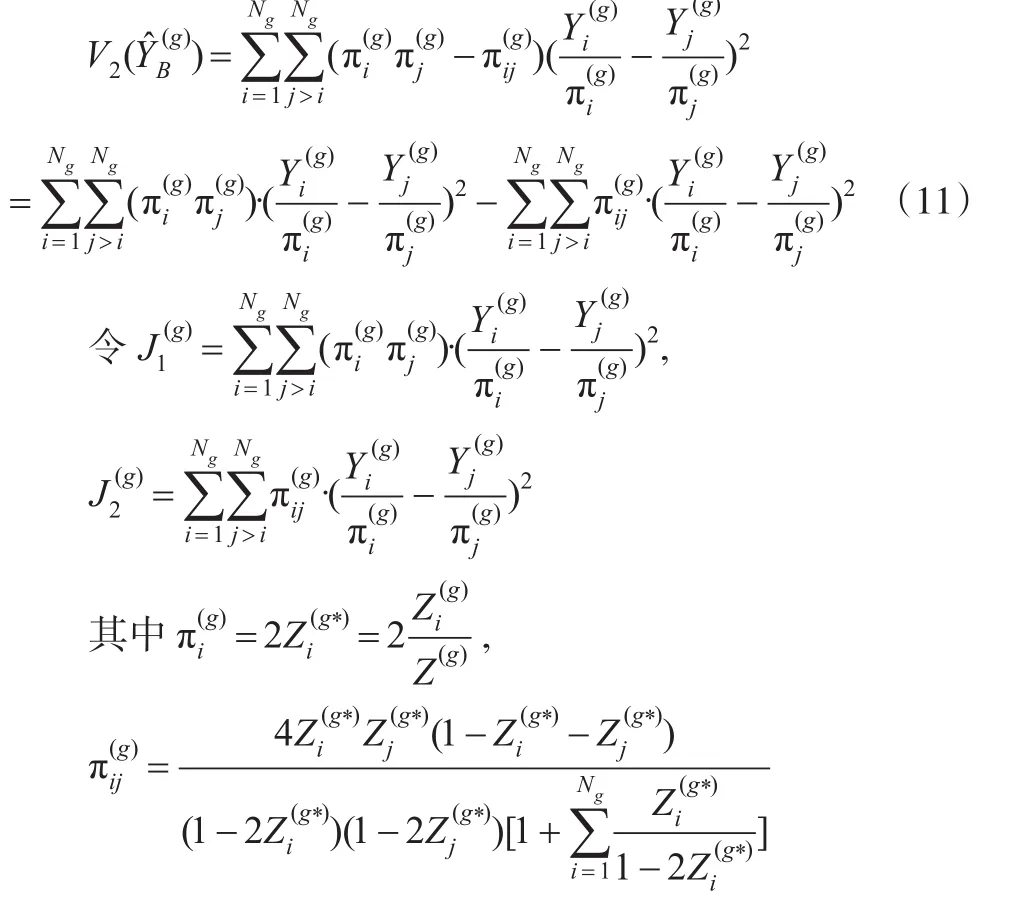
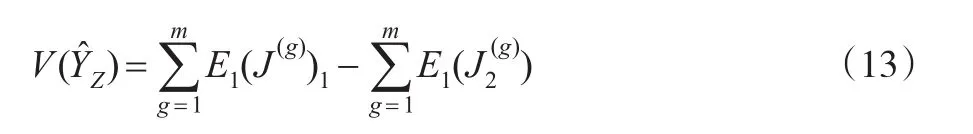
进一步化简因此：

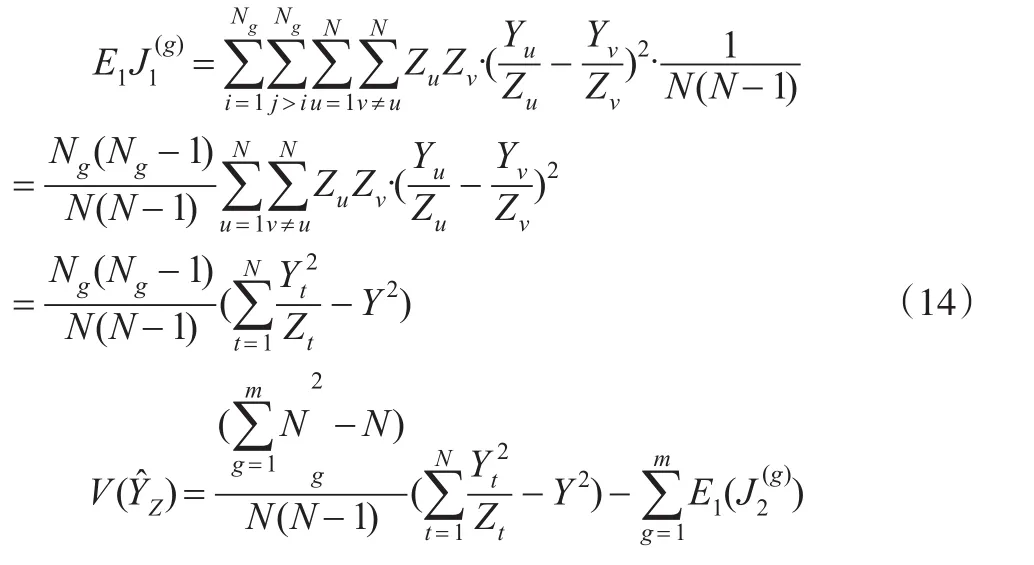
2.2 n为奇数的情形

将总体随机划分为m(=(n+1)/2)个组：记为G1，G2，…，Gm。在第g组Gg中,每个单元对应的Z值在此重新记为Zi(g),对应的Y值重新记为Yi(g),i=1，2，…，将每组中的Z值归一化记为

在每组Gg(1≤g≤m-1)中,按Brewer方法,抽取两个样本单元；在第m组Gm中按与，j=1，2，…，Nm成正比抽取一个单元,最后合成容量为n的样本s。

按Brewer方法,构造每组Gg(1≤g≤m-1)的总体总值的估计：

按Rao-Hartley-Cochran方法,构造最后一组Gm的总体总值的估计：

进而构造总体总值Y的估计：

利用Rao-Hartley-Cochran的结果和n为偶数时的结果直接可得：

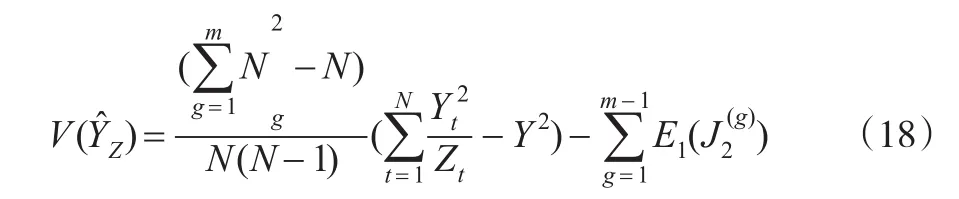
与条件泊松抽样、Rao-Hartley-Cochran方法比较，提出方法精度的改进，方差减少量的大小将通过数值模拟展示。

3 方差估计

条件泊松抽样下,对于总体总值Y的估计量ŶCP,根据Horvitz-Thompson估计量可以得到方差的一个无偏估计：

其中πi,πj,πij在第上文已给出相应的递推公式。

Rao-Hartley-Cochran针对估计量,提出了方差的一个无偏估计：

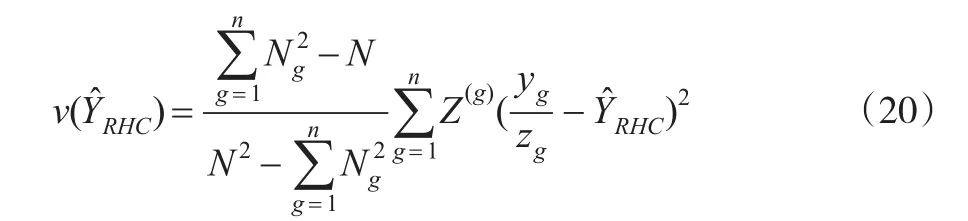
其中Z(g)是第g组Ng个单元Zi值的总和,yg是第g组抽到单元的观测值,相应的Z为zg。

对于本文提出的估计,提出其方差的一个无偏估计：

其中和是第g组抽到两个单元的观测值,相应的Zg*值为和

4 数值模拟

为了说明提出方法的优良性，本文基于不同超总体模型下的总体，利用Monte-Carlo模拟计算提出方法方差的第二部分或进而计算提出方法的方差和相对标准差。同样可以利用Monte-Carlo模拟计算条件泊松抽样方法的方差和相对标准差。

Rao-Hartley-Cochran方法的方差和相对标准差可以直接计算。调查变量根据八个不同的模型产生,每一个模型利用单变量回归函数产生E(yk|x)=fk(x)，k=1，…，8。本文考虑下列回归函数:

Linear:y1=1+2(x-0.5)+ϵ

Quadratic:y2=1+2(x-0.5)2+ϵ

Bump:y3=1+2(x-0.5)+exp(-200(x-0.5)2)+ϵ

Jump:y4=1+2(x-0.5)I(x≤0.65)+0.65I(x≥0.65)+ϵ

CdF:y5=Φ((0.5-2x)/0.02)+ϵ，其中Φ是标准正态分布函数

Exponential:y6=exp(-8x)+ϵ

Cycle1:y7=2+sin(2πx)+ϵ

Cycle4:y8=2+sin(8πx)+ϵ,其中x∈(0，1),参见文献[12]。

本文考虑x为一个有偏分布,实施模拟从Beta(66/49，165/49)分布独立同分布地产生。扰动变量ϵ～N(0，,为了保持调查变量y与辅助变量x的主要回归关系，正态扰动变量的方差的大小的选择为调查变量y的方差的1/5。对每一个模拟，按照提出的抽样设计和RHC设计以及条件泊松抽样设计，10000个样本针对不同的总体容量和样本容量产生。估计量和他们的方差估计被计算。通过下面的数量计算方法评价提出方法的性能。

的 Monte-Carlo 模拟为随机划分的一个实现。因此估计量

的方差的Monte-Carlo模拟为：

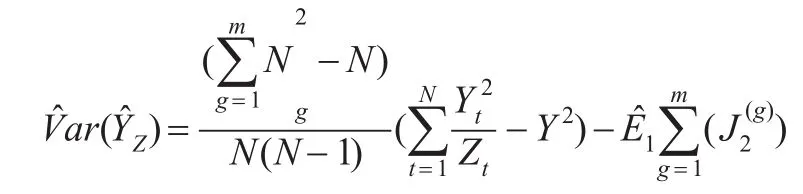
估计量的相对标准差为：

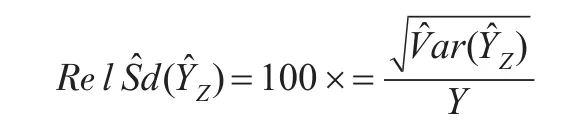
本文提出的方法与RHC方法、条件泊松抽样方法的效率比较情况如表1所示。

表1 RHC方法、条件泊松抽样的效率比较(N=60,n=6)

本文根据方差估计的相对方差和置信区间覆盖百分比对本文提出的方差估计和Rao-Hartley-Cochran提出的方差估计以及条件泊松抽样设计相应的方差估计进行评价。

一个方差估计$v$的相对方差：

置信区间覆盖百分比为：

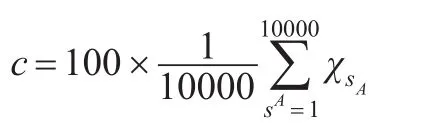
本文提出的方法与RHC方法、条件泊松抽样方法的方差估计比较情况如表2所示。

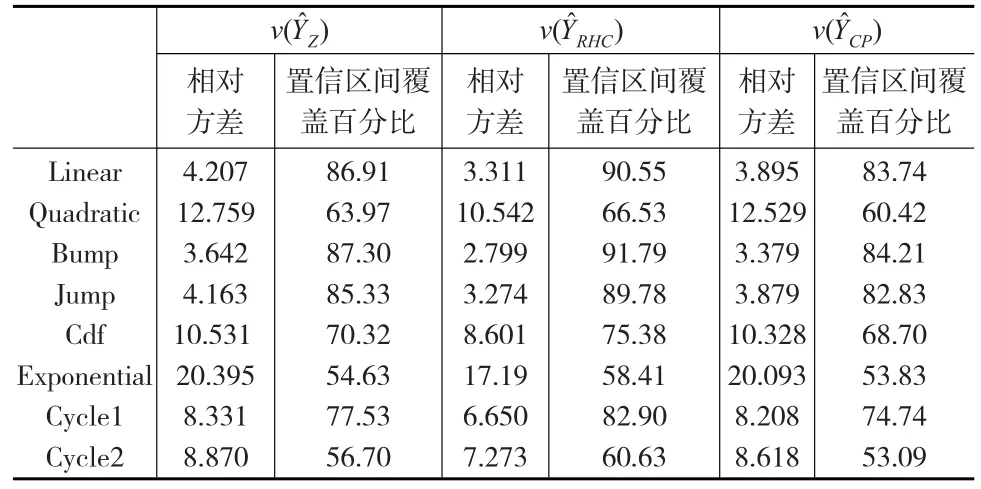
表2 提出方法、RHC方法、条件泊松抽样方法的方差估计比较(N=60,n=6)

5 结论

本文应用随机划分和Brewer方法,成功地设计了一种不等概率抽样设计，与经典的Rao-Hartley-Cochran的方法相比，调查精度能够达到RHC方法，具有实施方便简单的优点，主要解决了构造高精度的方差估计的难点问题。并且将本文提出的方法和条件泊松抽样方法进行了详细地比较，结果发现本文所提出的方法在精度上明显优于已有的条件泊松抽样方法，而且实施也较条件泊松抽样简单很多，方差估计也较条件泊松抽样简单，所以本文所提出的方法是一种很有实际应用价值的不等概率抽样方法。

参考文献：

[1]Horvitz D G,Thompson D J.A Generalization of Sampling Without Re⁃placement From a Finite Universe[J].Journal of the American Statisti⁃cal Association,1952,47（260）.

[2]Brewer K,Hanif M.Sampling With Unequal Inclusion Probabilities[M].New York：Springer-Verlag，1983.

[3]Zou G H,Feng S Y.A New Unequal Probability Sampling Design[C].Contributed Papers of 50th ISI,1995.

[4]Brewer K R W.A Model of Systematic Sampling With Unequal Proba⁃bilities～[J].Austral.J.Statist.,1963,（5）.

[5]Durbin J.Design of Multistage Surveys for the Estimation of Sampling Errors[J].Applied Statist,1967,（16）.

[6]Rao J N K,Harteley H O,Cochran W G.On a Simple Procedure of Un⁃equal Probability Sampling Without Replacement[J].Jour.Roy.Stat.Soc,1962,24（2）.

[7]Hajek J.Asymptotic Theory of Rejective Sampling With Varying Prob⁃abilities From a Finite Population[J].Annals of Mathematical Statis⁃tics,1964,（35）.

[8]Hajek J.Sampling From a Finite Population[M].New York:Marcel Dekker,1981.

[9]Grafstrom A.Repeated Poisson Sampling[J].Statistics and Probability Letters,2009,（79）.

[10]Laitila T,Olofsson J.A Two-Phase Sampling Scheme and πPS De⁃signs[J].Journal of Statistical Planning and Inference,2011,（141）.

[11]李苗苗,闫在在.条件泊松抽样下二阶包含概率的递归计算[J].应用数学学报,2014,37（1）.

[12]Montanari G E,Ranalli M G.Nonparametric Model Calibration Esti⁃mation in Survey Sampling[J].Journal of the American Statistical As⁃sociation,2005,100（472）.