城市住宅价格指数编制方法探讨

祁 炜

（北京师范大学 地理科学学部，北京 100875）

0 引言

住宅的异质性问题是房价指数编制中需要面对的重要问题。构成不同住宅价格的各个特征，如位置、楼层、朝向、小区环境、所在区域的交通状况、教育资源等，因缺乏统一的价格标准，无法直接进行比较，需要客观准确的方法对住宅价格进行合理评估。特征价格法较好地克服了市场比较法等传统方法中存在的问题，有较好的评估效果。国际上从20世纪80年代已经在房地产价格评估中采用这一方法，我国仍处于理论研究和实践的探索阶段。

本文以非线性Hedonic模型为基本模型。在影响住宅价格的各种因素中广泛地选择特征变量，进行显著性检验，通过显著性检验的特征作为特征价格模型的自变量保留，建立房价与特征变量之间的关系。选取足够的样本，运用传统的参数回归方法进行回归分析，检验模型的解释能力。通过对线性、半对数、对数等形式特征价格模型的对比分析，选取拟合度较好的模型，并采用Box-Cox变换进行优化，建立特征价格模型，并以武汉市新建商品住宅为例进行住宅价格指数编制。

1 武汉市房地产特征价格模型的建立

1.1 指标选取和数据描述

基于国内外研究经验及武汉市的城市特点，结合数据获取的难易程度，本文从住宅的区位特征、建筑特征、环境特征三方面综合选取了22个特征因素，加上时间变量，共量化为26个特征变量。具体解释如下页表1所示：

1.2 数据来源

（1）网签数据。房管部门备案登记的武汉市2015年1月至2016年5月期间的网签数据。网签数据中包含的特征变量有：住房价格、住房区位、所在楼层、层高类别和建筑结构。（2）国家统计局房价信息管理系统数据。包含的特征变量主要有：绿化率、容积率、车位比、开盘时间。（3）实地调查取得的补充数据。网签数据只能提供部分特征变量值，考虑到数据搜集的可操作性和数据的可获得性，通过抽样调查的方法补充网签和房价信息管理系统无法直接提供的特征值。主要包括楼盘交通情况、教育资源、休闲环境、商业环境等。

1.3 数据整理

1.3.1 分层抽样选取实地调查样本

采用精度控制下分层简单随机抽样的方法，在有网签数据的1707个楼盘中抽选94个样本楼盘。抽样方法如下：①精度控制：以1707个楼盘17个月网签数据为总体，控制总量指标的抽样精度，要求在95%的概率保证程度下，楼盘价格的最大相对误差控制在5%以内。②数据清理：在抽样之前，剔除网签数据中保障性住宅、存在明显登记错误的记录、累计销售套数在200以下和每月均价4000元以下的楼盘。③样本抽选：以各楼盘17个月成交均价为依据，采用累计平方根法确定分层界限，共分为5层，确定出本文所需样本数为94个。分配结果如下页表2所示。采用“永久随机数”方法抽取样本。

1.3.2 实地调查收集数据

根据建模指标设置需要，设计调查问卷，通过到有关部门走访和样本楼盘实地调研，了解商品住宅楼盘特征值。

1.3.3 数据整理和补缺

整合多渠道获得的数据，形成规范、统一、准确的数据库。由于部分楼盘在17个月的时间跨度中存在少数月份无销售的现象，造成该月价格缺失。在所抽取的94个楼盘17个月共1598个价格值中，缺失价格81个，占总量的5%，使用整理后的标准化未缺失房价数据和对应的特征值数据，运用人工神经网络方法进行建模。

1.3.4 数据标准化处理

对数据进行标准化处理主要为了避免数据性质不同和数据不可比的问题。不同性质和不可比指标直接加总不能正确反映不同作用力的综合结果，须先考虑改变逆指标数据性质，使所有指标对模型的作用力同趋化。代表异质性商品的基本功能；X为住房的n个特征；β为各个特征所对应的特征价格；t为反映住房价格中时间影响的系数；Dt为住房在t期的哑元变量；ε为随机误差项。

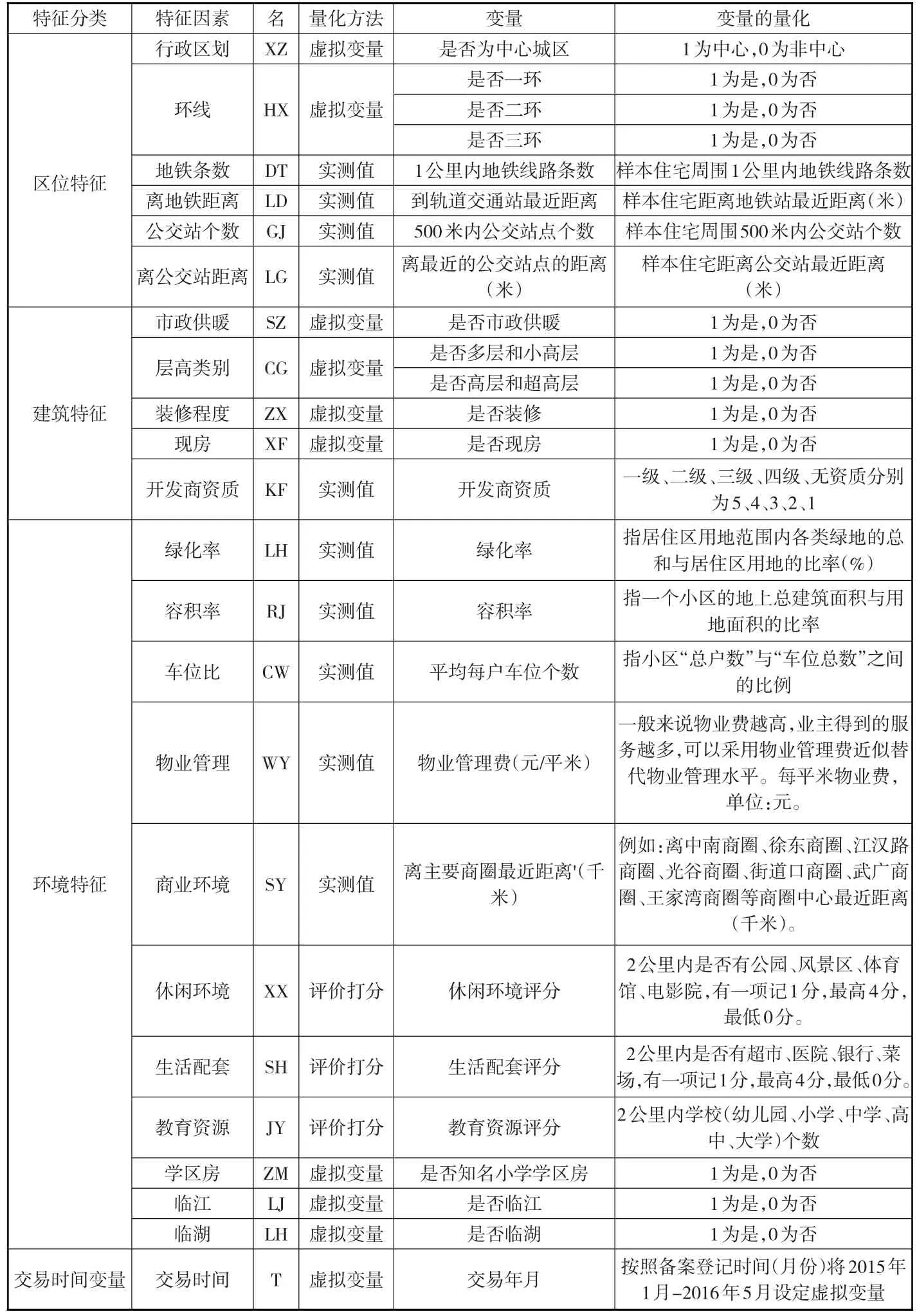
表1 特征价格模型常用解释变量

表2 分层抽样每层所需样本数

1.4.1 模型形式选取

本文首先构建Hedonic模型的线性、对数和半对数形式。由表3可知，总体来看，半对数形式的Hedonic模型最优，因此，本文选择半对数Hedonic模型继续进行指数测算。

半对数Hedonic模型的拟合优度检验：方程的相关系数为0.928，调整后的判定系数R2为0.859，模型能够解释因变量差异的85.9%。该模型在特征价格拟合程度上具有良好的解释能力。

回归模型总体显著性检验：方差分析的检验统计量F值为407.434，在概率小于0.01拒绝自变量系数均为0的原假设下，表明进入模型的自变量对因变量的共同影响具有显著性，回归方程总体有效。

1.4.2 特征变量显著性检验

基于构建的半对数形式Hedonic模型，对选取的26个变量进行显著性检验，结果见下页表4。

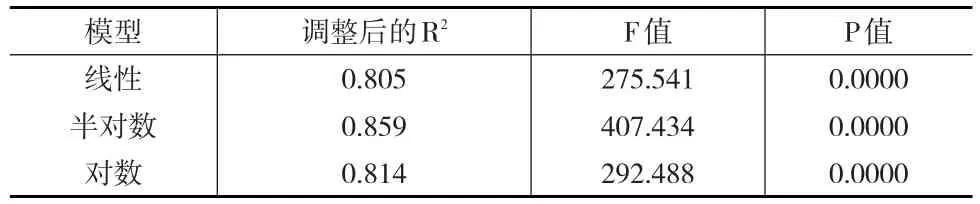
表3 三种形式的Hedonic模型统计量对比

除“学校个数”、“休闲得分”、“生活得分”和“离最近公交站点距离”外，其他特征变量的回归系数在10%显著水平下均

1.4 Hedonic模型的建立和选取

一般而言，Hedonic模型有线性、半对数、对数和Box-Cox变换等多种形式，在构建模型过程中，通过测算选出拟合度较好的模型形式。特征价格法基本模型如下：

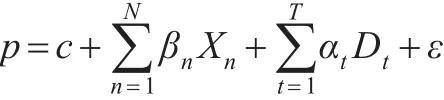
其中，p为异质性商品的市场价格；c为模型常数项，能通过t检验，表明模型中所选的特征变量具有较好的显著性。

多重共线性检验：各特征变量的方差膨胀因子VIF均小于5，绝大多数小于2，可以认为模型中不存在明显的多重共线性问题。

由半对数形式模型运算得到残差图，模型的残差近似正态分布，构建的半对数Hedonic模型对武汉市的住宅价格具有较高的拟合优度和较好的解释能力，可以解释该市楼盘特征变量对住宅价格的影响。

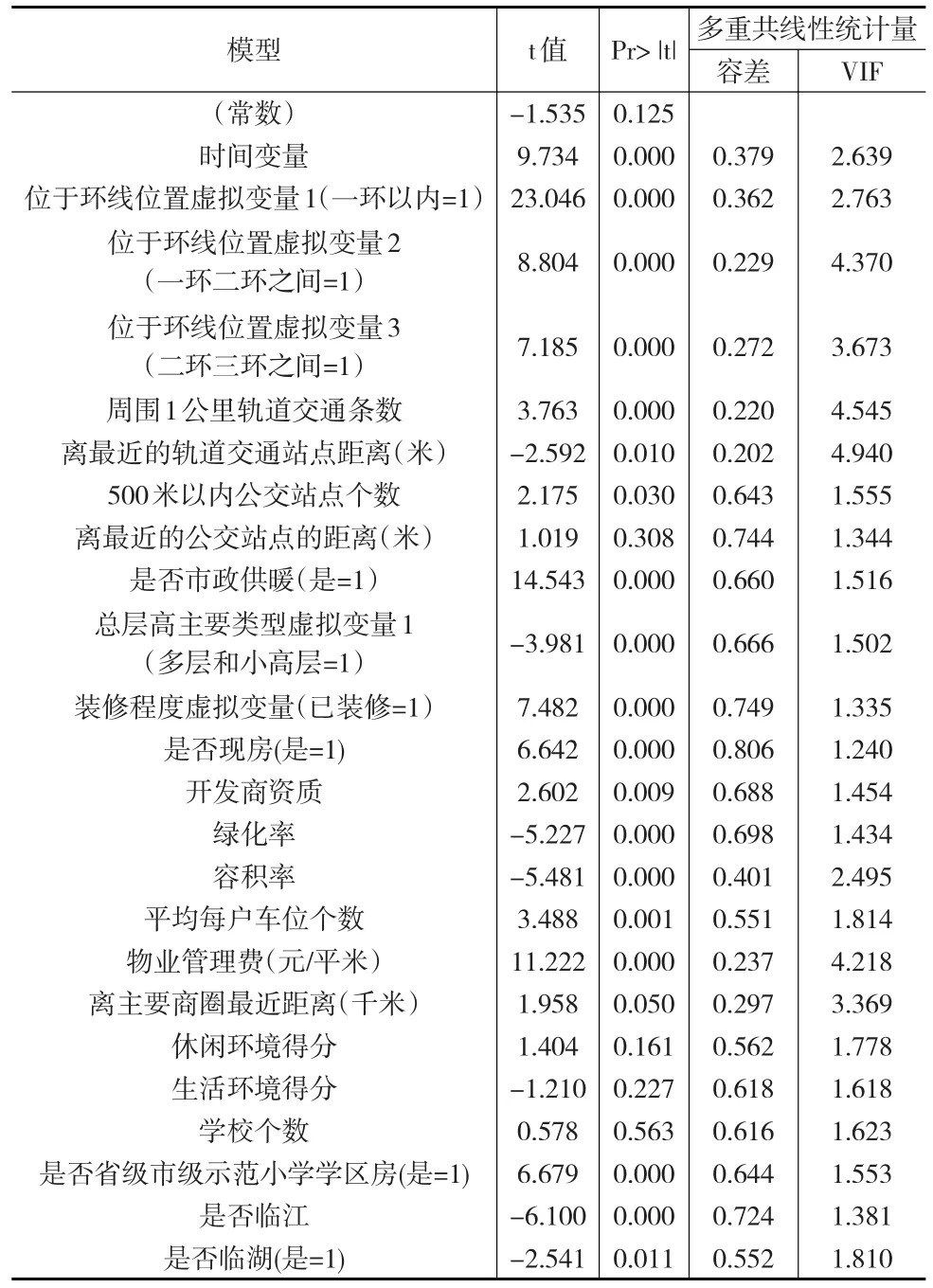
表4 半对数Hedonic模型系数的显著性检验

1.4.3 分月价格指数的计算

（1）确定标准住宅。标准住宅代表着市场上住宅的普遍水平，标准住宅的选取，是消除住宅异质性的关键。样本楼盘在选取时充分考虑了代表性，本文以考察的17个月中各个特征变量的平均值作为市场存在的普遍水平，代表本区域房地产市场的标准住宅。

（2）测算指数对比。把标准住宅的各个特征值代入17个分月半对数Hedonic模型，得到各月的标准住宅价格。17个标准住宅价格消除了住宅价格的异质性（特征差异），具有同质可比性，当月价格比上月价格即可得到当月房地产价格环比指数，见表5。

表5 2015年1月至2016年5月武汉市商品住宅特征价格指数计算结果

图1半对数Hedonic模型编制环比与国家公布指数对比

通过半对数Hedonic模型测算，所得环比指数呈震荡上行态势，幅度在-5.7%～6.9%之间波动。国家统计局每月公布环比指数处于温和上涨态势，涨幅在0%～2.3%之间。对比发现（见图1）半对数Hedonic模型测算结果与国家公布数据总体趋势一致，17个月测算环比指数围绕国家统计局公布指数上下波动，少数月份与公布指数完全吻合，超五成月份与公布指数涨跌趋势存在一定差异。对于存在的这种差异，将进一步通过Box-Cox变换进行优化，以达到更优的效果。

1.5 模型优化

将半对数形式的因变量进行Box-Cox变换，运用R软件，可以得到λ最优值，其最优值为λ=-0.15。回归结果显示，Box-Cox变换的半对数形式模型回归结果中，各特征变量系数基本与预期影响相符，在10%的显著性水平下，26个变量中除“周围1公里轨道交通条数”、“总层高”和“平均每户车位个数”三个特征变量外，其余特征变量均具有较好的显著性。

拟合优度检验结果表明，回归模型的相关系数为0.89，调整后的判定系数R2=0.789，表明模型能够解释因变量差异的78.9%，拟合程度较好。

回归模型的总体显著性检验表明，方差分析检验统计量F值为260，在概率小于0.01拒绝自变量系数均为0的原假设下，表明进入模型的自变量对因变量的共同影响具有显著性，回归方程总体有效。

多重共线性检验结果表明，各自变量的方差膨胀因子均小于5，表明模型中不存在明显的多重共线性。模型残差近似正态分布。

综上所述，构建的武汉市商品住宅Box-Cox变换的半对数形式特征价格模型具有良好的拟合优度和较高的解释能力，各特征变量的回归系数具有统计意义上的显著性，通过统计检验，可以用来分析住宅特征变量对住宅价格的影响。

按照上述各步骤，可以得出武汉市17个月的分月住宅特征价格模型。

下页图2是采用半对数和Box-Cox变换的半对数模型编制出的住宅价格指数与国家公布指数的比较。通过Box-Cox变换的半对数模型测算所得环比指数呈震荡上行态势，幅度在-3.92%～5.14%之间波动，与之前的半对数模型相比变化幅度缩小，17个月环比指数据中超五成月份与国家公布指数涨跌趋势一致，整体来看更接近国家公布的环比指数趋势。

图2不同方法编制的住宅价格指数比较

2 结论和展望

2.1 主要结论

（1）数据来源更加全面准确有效。本模型以武汉市房管局提供的网签数据为基础，比网络搜索和网络爬虫方法获取的数据更为准确。通过实地采访调研的方式获取楼盘特征值，补充网签数据无法提供的房地产特征，构建了较为完整的住宅价格特征变量体系。采用在一定精度控制保证下分层抽样方法抽取楼盘样本，确保了实地调查样本的代表性。

（2）对特征价格模型的线性、半对数、对数、Box-cox变换模型形式进行对比分析。在真实的市场交易中，住宅价格受多方面因素共同影响，与各个特征变量之间并不是简单的线性关系，因此，本文在线性模型的基础上引进了半对数、对数和Box-Cox变换模型，更全面地考量了住宅价格和各个特征变量之间的关系。

（3）以楼盘为样本单位，避免了以个体住宅为样本的缺陷。楼盘均价能较好地反映住宅价格分布结构。当前，国内外研究多以住宅为样本单位，这种做法存在一定缺陷。一是住宅的朝向、景观等特征值收集困难；二是若某研究时间段内，具有同一特征因素的住宅销售量占比过大时，该特征值会产生较大影响，造成这些特征值相关度过大。以楼盘为研究对象可以平滑影响。

2.2 研究展望

本文为研究城市住宅价格提供了一种统计技术上的有益探索，但离全面深入运用Hedonic模型编制住宅价格指数还有一段距离，因此对Hedonic模型及其应用的研究还得继续。第一，本文在建模时楼盘价格仍使用混合平均价，没有实现用楼盘标准价进入模型，在后续研究中，将进一步探索用楼盘标准价进行建模测算；第二，可尝试非参数、半参数等多种参数估计方法在模型中的运用；第三，进一步探索对大数据的匹配、筛选、挖掘等预处理的有效方法。

参考文献：

[1]Case B,Pollakowski H O,Wachter S M.On Choosing Among House Price Index Methodologies[J].AREUEA Journal,1991,19(3).

[2]程亚鹏.基于住房子市场的Hedonic住房价格指数[J].经济问题，2010，(10).

[3]李占风,周歆毅.我国房地产价格的统计方法研究[J].统计与决策,2012，(8).

[4]孙玉环.基于海量交易数据的房地产特征价格模型的构建[J].统计与决策,2011，(10).

[5]程亚鹏.我国城市住宅价格测试—Hedonic方法与实证[M].北京:光明日报出版社,2013.