函数与导数综合应用专题测试卷B

■河南省南阳市第五中学 代志杰

已知(){-lgx,x＞0,且()

1.fx=ax+b,x≤0f0=2,f(-1)=4,则f(f(-2))=( )。

A.-1 B.2 C.3 D.-3

2.已知函数f(x+1)的定义域为[-2,3],则f(3-2x)的定义域为( )。

A.[-5,5]

B.[-1,9]

3.已知定义在R上的函数f(x)满足f(x-3)=-f(x),在区间上是增函数,且函数y=f(x-3)为奇函数,则( )。

A.f(-31)＜f(84)＜f(13)

B.f(84)＜f(13)＜f(-31)

C.f(13)＜f(84)＜f(-31)

D.f(-31)＜f(13)＜f(84)

4.已知f(x)=ax2+bx+3a+b是偶函数,定义域为[a-1,2a],则a+b=( )。

5.已知映射f：A→B,其中A={x|x＞0},B=R,对应法则f：x→-x2+2x,对于实数k∈B,在集合A中存在两个不同的原象,则k的取值范围为( )。

A.k＞0

B.k＜1

一、选择题

C.0＜k≤1

D.0＜k＜1

7.若幂函数y=xm是偶函数,且x∈(0,+∞)时为减函数,则实数m的值可能为( )。

A.-2

D.2

A.(0,1)

9.小明骑车上学,一路匀速行驶,只是在途中遇到了一次交通堵塞,耽搁了一些时间。与以上所述情况吻合得最好的图像是图1中的( )。

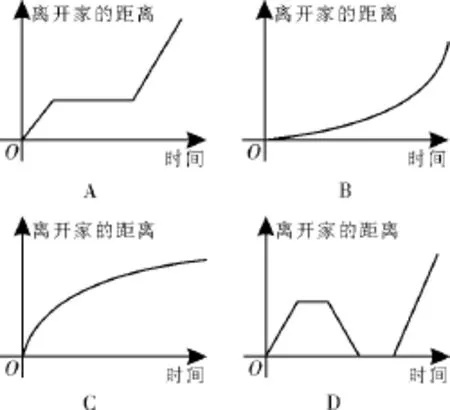
图1

10.设偶函数f(x)的定义域为R,当x∈[0,+∞)时f(x)是增函数,则f(-2),f(π),f(-3)的大小关系是( )。

A.f(π)＜f(-2)＜f(-3)

B.f(π)＜f(-3)＜f(-2)

C.f(π)＞f(-2)＞f(-3)

D.f(π)＞f(-3)＞f(-2)

11.函数f(x)是定义在R上的奇函数,当x＞0时,f(x)=-x+1,则当x＜0时,f(x)=( )。

A.-x+1

B.-x-1

C.x+1

D.x-1

12.下列函数中,既是奇函数又存在零点的是( )。

A.y=cosx

B.y=sinx

C.y=lnx

D.y=1x

13.已知f(x)满足∀x∈R,f(-x)+f(x)=0,且x≥0时,f(x)=ex+m(m为常数),则f(-ln5)的值为( )。

A.4 B.-4 C.6 D.-6

14.设a=log34,b=log0.43,c=0.43,则a,b,c的大小关系为( )。

A.c＞a＞b

B.a＞c＞b

C.b＞c＞a

Dc.＞b＞a

15.已知函数f(x)=1-x+log1-x,21+x则的值为( )。

16.函数f(x)=log2(3x+1)的值域为( )。

A.(0,+∞) B.[0,+∞)

C.(1,+∞)D.[1,+∞)

17.在下列区间中,使函数f(x)=存在零点的是( )。

A.(0,1) B.(1,2)

C.(2,e) D.(3,4)

18.设a∈R,若函数y=eax+2x,x∈R有大于零的极值点,则( )。

Aa.＜-2 Ba.＞-2

19.设函数f'(x)是函数f(x)(x∈R)的导函数,f(0)=1,且3f(x)=f'(x)-3,则4f(x)＞f'(x)的解集为( )。

20.已知定义在R上的可导函数f(x)的导函数为f'(x),满足f'(x)＜f(x),且f(x+3)为偶函数,f(6)=1,则不等式f(x)＞ex的解集为( )。

A.(-∞,0) B.(0,+∞)

C.(1,+∞) D.(4,+∞)

A.|2p(t1-t2)|

B.2p(t1-t2)

22.将曲线y2=4x按变换后得到的曲线的焦点坐标为( )。

C.2 D.-2

24.已知函数y=f(x)和y=g(x)在[-2,2]上的图像如图2和图3所示,给出下列四个命题：

图2

图3

(1)方程f[g(x)]=0有且仅有6个根;

(2)方程g[f(x)]=0有且仅有3个根;

(3)方程f[f(x)]=0有且仅有5个根;

(4)方程g[g(x)]=0有且仅有4个根。

其中正确命题的个数为( )。

A.1 B.2 C.3 D.4

25.如果关于x的不等式|x+1|+|x+2|＜k的解集不是空集,则实数k的取值范围是( )。

A.1 B.2 C.3 D.4

26.调查表明,酒后驾驶是导致交通事故的主要原因,交通法规规定：驾驶员在驾驶机动车时血液中酒精含量不得超过0.2mg/mL。如果某人喝了少量酒后,血液中酒精含量将迅速上升到0.8mg/mL,在停止喝酒后,血液中酒精含量就以每小时50%的速度减少,则他至少要经过( )小时后才可以驾驶机动车。

A.1 B.2 C.3 D.4

27.函数f(x)=log2x与g(x)=在同一直角坐标系中的图像是图4中的( )。

图4

二、填空题

28.已知函数f(x)=无论t取何值,函数f(x)在区间(-∞,+∞)上总是不单调,则a的取值范围是____。

29.已知函数f(x)=则(lo12)=____。fg2

30.幂函数f(x)=(m2-3m+3)·xm2-2m+1在区间(0,+∞)上是增函数,则m=____。

31.已知2x=5y=10,则

32.函数y=log2x,x∈(0,16]的值域是____。

34.化简(log43+log83)(log32+log92)=____。

36.已知函数f(x)=aln(x+1)-x2,若在区间(0,1)内任取两个实数p,q,且p≠q,不等式恒成立,则实数a的取值范围为____。

37.已知函数f(x)=lnx+x,若函数f(x)在点P(x0,f(x0))处的切线与直线3x-y+1=0平行,则x0=____。

三、解答题

42.已知f(x)=ex-ax2,曲线y=f(x)在(1,f(1))处的切线方程为y=bx+1。

(1)求a,b的值;

(2)求f(x)在[0,1]上的最大值;

(3)证明：当x＞0时,ex+(1-e)xxlnx-1≥0。

(1)求函数f(x)的零点及单调区间。

44.已知函数f(x)=(a-1)2lnx+(a-1)x+3(a≠1)。

(1)求函数f(x)的单调区间。

(2)若函数f(x)在区间(1,2)内单调递增,求实数a的取值范围。

45.已知函数f(x)=x3+ax2+bx+c,曲线y=f(x)在点x=-1处的切线为l：5x+y-5=0,若时,y=f(x)有极值。

(1)求a,b,c的值;

(2)求y=f(x)在[-3,2]上的最大值和最小值。

46.已知函数f(x)=loga(x+1),g(x)=loga(4-2x)(a＞0,且a≠1)。

(1)求函数f(x)-g(x)的定义域;

(2)求使函数f(x)-g(x)的值为正数的x的取值范围。

47.已知函数f(x)=2x2-4x+a,g(x)=logax(a＞0且a≠1)。

(1)若函数f(x)在[-1,2m]上不具有单调性,求实数m的取值范围;

(2)若f(1)=g(1)。

①求实数a的值;

48.已知函数f(x)=log2(1+x)+alog2(1-x)(a∈R)的图像关于y轴对称。

(1)求函数f(x)的定义域;

(2)求a的值;

(3)若函数g(x)=x-2f(x)-2t有两个不同的零点,求实数t的取值范围。

49.将圆x2+y2=1上每一点的横坐标保持不变,纵坐标变为原来的2倍,得到曲线C。

(1)写出曲线C的参数方程;

(2)设直线l：2x+y-2=0与曲线C的交点为P1,P2,以坐标原点为极点,x轴的正半轴为极轴建立极坐标系,求过线段P1P2的中点且与l垂直的直线的极坐标方程。

(1)将C1,C2的方程化为普通方程;

(2)若C1上的点P对应的参数为t=为C上的动点,求PQ的中点M到直2线的距离的最小值。