在“意译”中培养思维能力，提升逻辑推理数学素养

☉江苏省金湖中学 陈万斌

逻辑推理是指从一些事实和命题出发，依据逻辑规则推出一个命题的思维过程.主要包括两类：一类是从特殊到一般的推理，推理形式主要有归纳、类比；一类是从一般到特殊的推理，推理形式主要有演绎.逻辑推理是得到数学结论、构建数学体系的重要方式，是数学严谨性的基本保证，是人们在数学活动中进行交流的基本思维品质.

在逻辑推理核心素养的形成过程中，教师要教会学生对问题进行“直译”外，更加注重教会学生对问题进行“意译”，“意译”更能培养学生的理性思维能力，同时教师要引导学生能够发现问题和提出命题；教会学生掌握推理的基本形式，表述论证的过程；培养学生关于数学知识之间的联系和建构知识框架的意识；形成有论据、有条理、合乎逻辑的思维品质，增强数学交流能力.

一、观察式子外在特点，采用变化推理解题

例1定义在R+上的函数f（x），满足f（x）+xf′（x）＞0，求不等式f（x+1）＞（x-1）f（x2-1）的解集.

解析：由f（x）+xf′（x）＞0可知［xf（x）］′＞0.

令g（x）=xf（x），知g（x）是（0，＋∞）上的增函数，所以f（x+1）＞（x-1）f（x2-1），所以（x+1）f（x+1）＞（x2-1）f（x2-1），即g（x+1）＞g（x2-1）.

评议：对式子进行变形，合乎推理条件.

例2 已知M（-1，0），P是圆C：x2+y2-6x+1=0上的动点.

评议：对等式进行变化，抓住条件推出结论.

例3 设数列｛an｝满足且对任意的正整数n，满足an+2-an≤3n，an+4-an≥10×3n，求a2016的值.

解析：因为an+4-an≥10×3n，又an+4-an=an+4-an+2+an+2-an≤3n+2+3n=10×3n，则an+4-an=10×3n且an+2-an=3n.

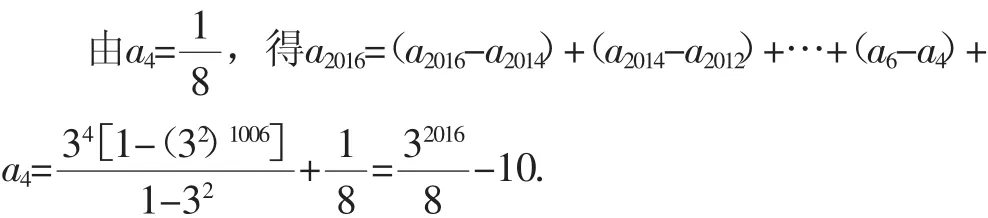
评议：分析两个不等式的特点，进行综合推理.

二、抓住图形内含条件，进行转化推理解题

例4 如图1，已知直线l1：mx+y-1=0过定点A，直线l2：x-my+2+m=0过点B，直线l1与直线l2的交点为P，求PA+PB的范围.

解析：由题意可知A（0，1），B（-2，1）.

又l1⊥l2，所以∠APB=90°，AB=2.

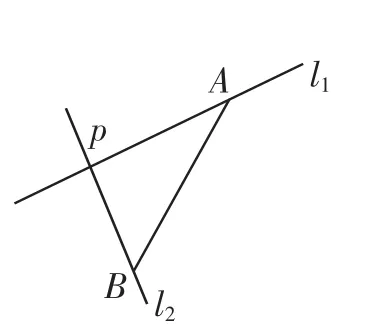
图1

评议：分析习题的内在条件，合理解决.

例5 已知A（-3，-4），B（0，-1），求∠AOB的平分线所在直线的方程.

解析：由已知条件可知OA=5，OB=1.

因为OC=OA，所以平行四边形OAMC为菱形，如图2所示.

故∠AOB的平分线为直线OM，即方程为y=3x（x＜0）.

评议：利用角平分线的性质，创造推理的条件.

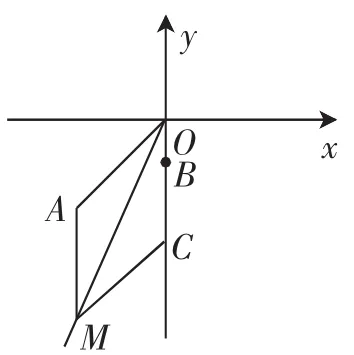
图2

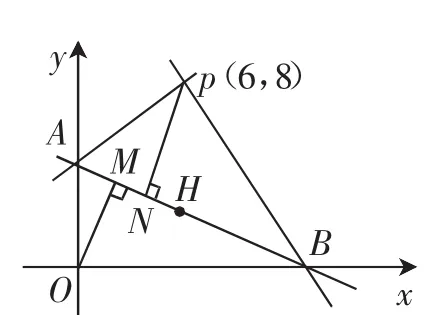
图3

例6 已知过点P（6，8）的直线l1和l2，且l1⊥l2，l1与y轴交于点A，l2与x轴交于点B，满足S△AOB=S△PAB，求直线AB的方程.

解析：如图3，过O点作OM⊥AB，过P点作PN⊥AB，垂足分别为点M，N.

所以Rt△PHN≌Rt△OHM，所以HM=HN.

点M与N重合或者H为MN的中点，可知点M（3，4）且N（3，4）或者H（3，4），B（6，0）.

评议：对条件进行联想，合情推理.

三、挖掘习题隐形本质，利用内化推理解题

例7已知f（x）=x3+ax-a2x+2，如对于一切x1，x2，x3∈［0，1］，总存在以f（x1），f（x2），f（x3）为三边长的三角形，求正实数a的取值范围.

解析：分析题意可知f（0）＜f（1）+f（1），解得0＜a＜2.

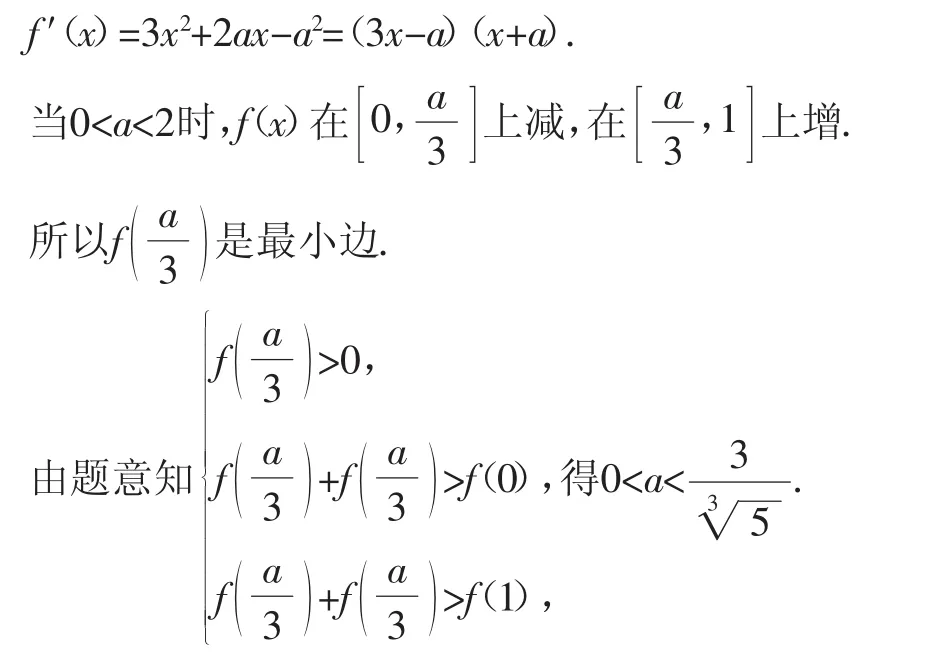
评议：分析问题得出本质，推出方法.

例8 如图4，在平面直角坐标系xOy中，圆C的方程为x2+y2-4x=0，若直线y=k（x+1）上存在一点P，使过点P所作的圆的两条切线相互垂直，求实数k的取值范围.

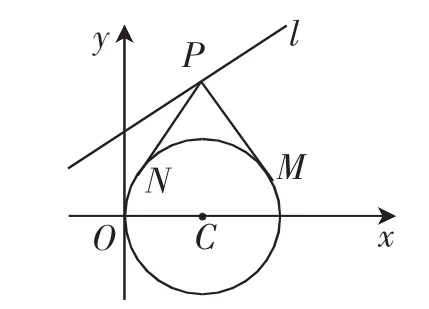
图4

评议：分析问题的内涵，优化推理.

例9 若直角坐标平面内两点P，Q满足条件：（1）P，Q都在函数f（x）图像上；（2）P，Q关于原点对称，则对称点（P，Q）是函数f（x）的一个“友好点对”（点对（P，Q）与（Q，P）看作同一个“友好点对”）.

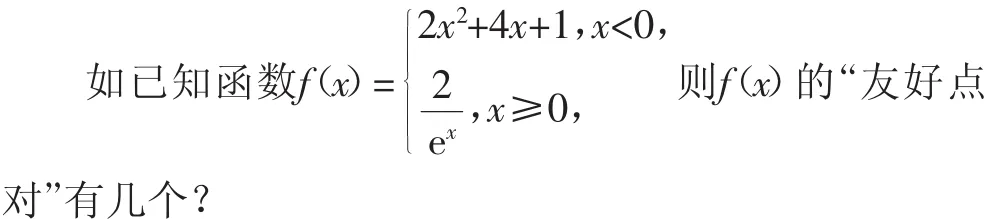
解析：可画出f（x）的示意图，如图5.

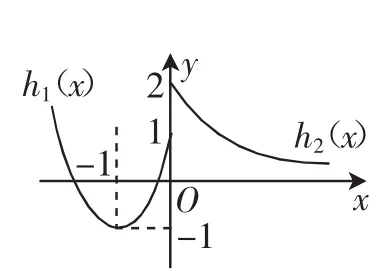
图5

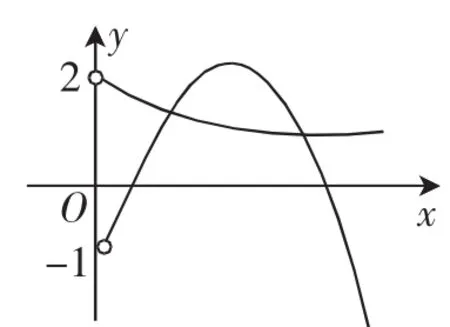
图6

由题意可设函数g（x）图像与函数h1（x）图像关于原点对称，本题变为只求函数y=g（x）与函数y=h2（x）的图像交点个数即可，由图6知有两个交点，所以f（x）的“友好点对”有2个.

评议：审视题意，合情推理

四、采用不同解题策略，深化逻辑推理素养

解析：g′（x）=x2+（m+4）x-2.

如函数g（x）在（1，3）内是单调的，即在（1，3）内是递增或递减的，则当1＜x＜3时，g′（x）≥0或g′（x）≤0恒成立，所以-（m+4）≤或-（m+4）≥恒成立，解得m≥-3或m≤

评议：审视习题，思维发散.

例12 在数列｛an｝中，a1=m（m为正整数），an+1=

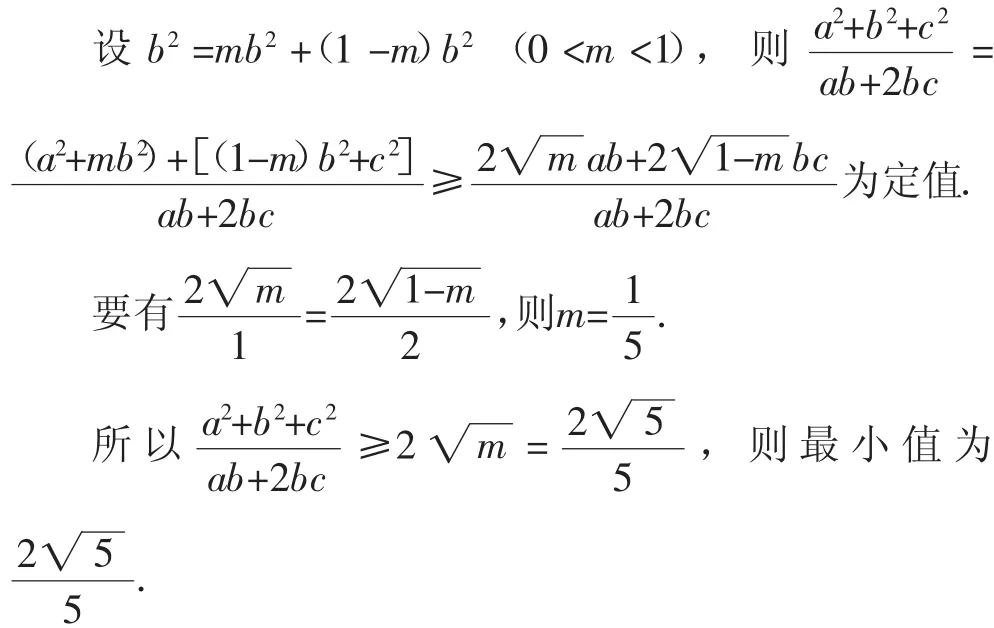
解析：把b2分解成两部分，如何分解成为解决问题的关键.

评议：反之逐级推理

逻辑推理的核心是培养学生善于分析、规范推理、合乎逻辑的思维品质，是培养学生数学严谨性、思维的、条理性的途径，也是学生进行建构数学、重视推理过程、体验成果、感受成功快乐的渠道，更是培养学生发现问题、探索问题、增强交流合作意识的手段，学生只有在老师长期引导和合作下，逻辑推理的数学素养定能加强和深化.

1.章建跃.数学核心素养如何落实在课堂［J］.中小学数学（高中版），2016，（3）.F