高三数学课堂复习课教学实践与思考

☉江苏省苏州市吴江汾湖经济开发区高级中学 王 铮

高三数学第一轮复习怎样才能提升复习质量是高三数学老师都尤其关心的问题，本文结合“平行位置关系”这一内容复习过程的分析与研究就如何提升高三复习课教学谈几点笔者的思考.

一、教学目标设置

课题：空间平行位置关系

教学目标：（1）通过本课的教学、分析与拓展使学生能够了解直线、平面各空间领域中平行的定义、判定定理、性质以及逻辑推理关系；（2）使学生能够理顺其逻辑关系的基础上解决平行问题的证明.

教学重点：平行的定义、判定定理、性质定理的理解与应用.

教学难点：灵活应用及证明.

二、过程实录

1.知识梳理

将表1投影并引导学生对它们的定义、判定、性质进行分别阐述.

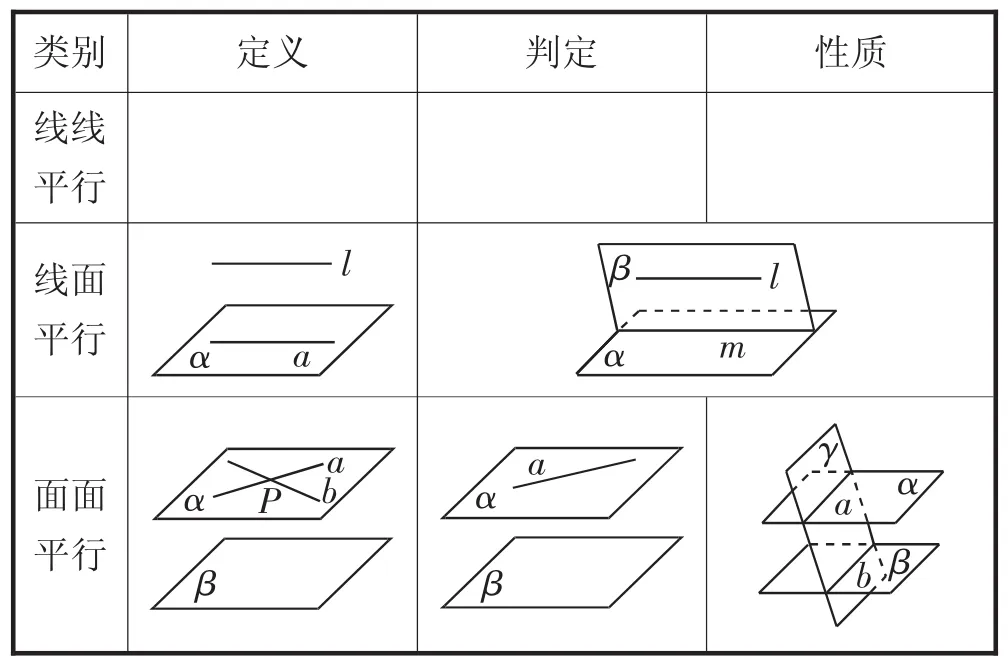
表1

教师在投影的同时将如图1所示的三种平行关系的三角形结构一并在画在黑板上，并注意在所有概念复习之后再引导学生将视点重新聚焦在此结构图中，引导学生对三种平行位置之间蕴含的联系进行思考、挖掘和阐述.

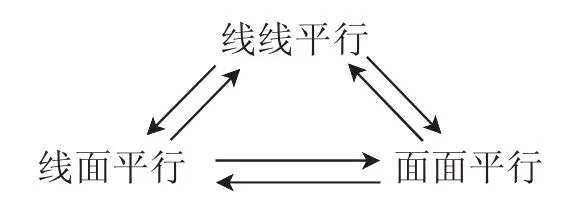
图1

点评：大多教师在传统的复习中都会按照直线之间、直线与平面、平面之间的位置关系这一顺序进行各个知识版块的复习.但此课的复习却转换了思路：将所有的平行位置关系罗列在了一起进行复习，展现出了更强的知识系统性，各个空间领域的平行位置关系的发生、发展也被更加彻底而全面地展示出来.若想证明平面之间的平行必须通过直线与平面平行来达成、直线与平面平行则需要证明直线之间的平行来达成这样的通性通法也得到了更好的强化，学生对平行位置关系的证明与运用也会更加牢固.而且，此课对重点知识的梳理采取了表格的方式，知识发展的脉络、学生对知识点共性特征的感悟也在完整的知识体系中更加清晰和完整.

2.基础训练

有a、b两直线与α、β两平面，请尝试判断下列哪些命题是真命题，哪些命题是假命题.所有假命题请举出反例来说明，所有真命题请阐述真确的理由.

（1）若a⊂α，b∥a，则b∥α；

（2）若a∥α，则a平行α内任一直线；

（3）若a∥α，b∥α，a⊂β，b⊂β，则α∥β；

（4）若α∥β，b⊂α，则b∥β；

（5）若a∥α，b∥α，则a∥b.

请学生对以上基础练习进行一一回答并结合教室中的线、面进行具体的理由阐述，教师适时作出点评以帮助学生形成正确的认知.

点评：这样的原题训练能够帮助学生在判断、矫正中加深对概念的理解，很多学生原本模棱两可的认知随着解题的推进一步步得以明晰.

教师在发现学生错误认知时应充分利用教室的墙角线进行说明，学生在直观、形象的具体讲解中也使得实际问题得到了有效的解决.

3.例题分析

例1 如图2，在四棱锥P-ABCD中，底面ABCD是平行四边形，PC、AB的中点为E、F，求证：EF∥平面PAD.

教师在给出题目之后并没有将解法直接呈现给学生，也没有很突兀地让学生独立自主解题，而是引导学生根据判定定理在平面PAD中寻找与EF平行的直线，或者引导学生根据定义构造经过EF并与平面PAD平行的平面.在帮助学生明晰探究的方向之后再放手让学生自主探究本题的解决途径，教师巡视学生解题时特别注重观察学生的具体解法，并请学生上黑板演示两种有代表性的解法.

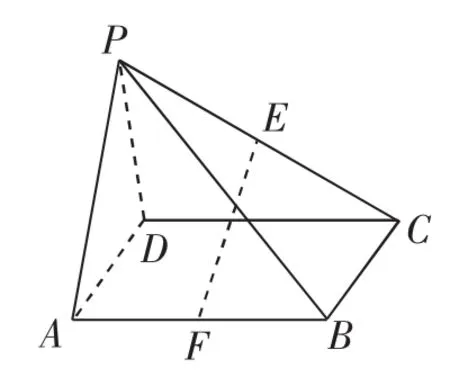
图2

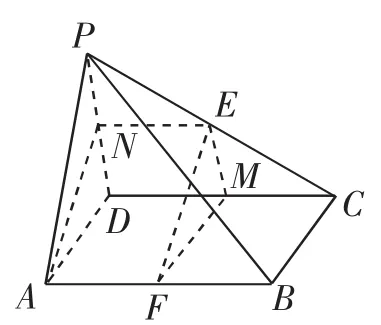
图3

生1：如图3，取PD中点N并连接AN、NE.由题设知，NE为△PDC的中位线，则.四边形ABCD是平行四边形，AB中点为F，则，故NE=AF，所以NEFA为平行四边形，EF∥AN.而EF⊄平面PAD，AN⊂平面PAD，所以EF∥平面PAD.

生2：如图3，取DC中点M并连接EM、FM.由题设知，EM∥PD，而EM⊄平面PAD，PD⊂平面PAD，所以EM∥平面PAD.又四边形ABCD是平行四边形，AB、DC中点为F、M，所以AFMD是平行四边形，FM∥AD.而FM⊄平面PAD，AD⊂平面PAD，所以FM∥平面PAD.又FM∩EM=M，所以平面EFM∥平面PAD，即平面EFM与平面PAD无公共点.又EF⊂平面EFM，所以EF与平面PAD无公共点，则EF∥平面PAD.

教师在此题探究结束之后再次将定义法与判定定理法这两个证明线面平行的基本方法进行总结，强调书写规范与逻辑严谨性的同时启发学生在掌握通性通法的基础上探求新的证明方法，生3与生4的方法也由此产生，要点如下：

生3：延长DA并使其延长线与CF的连接线相交于K，证明EF∥PK.

生4：取PB中点G，连接EG、FG，证明平面EFG∥平面PAD.

点评：教师所选的这个例题紧紧围绕教学目标且富含教育功能，有助于教学目标的实现与学生思维活动的开展，学生在这种入口宽、方法灵活的例题中进行探究与思维训练也能更好地掌握线面平行的基本方法.教师的剖析与引导、学生的自主探索与思考在例题教学中都是尤其重要的.因此，教师在教学中应适时引领学生对证明的过程进行及时的回顾与分析，使学生在自己感悟思维规律的同时掌握基本方法并逐步学会举一反三与灵活应变.

例2 如图4，在三棱柱ABC-A1B1C1中，O、H是A1C、B1C1的中点，求证：OH∥平面ABB1A1.

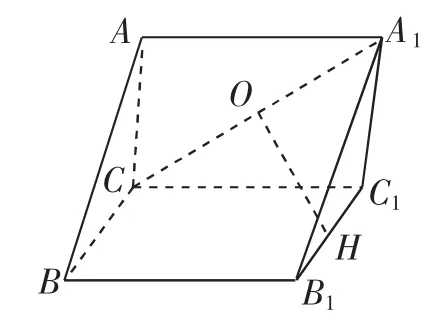
图4

例1的教学重点在于解题过程的思维剖析和书写规范，本题的教学立意在于引导学生在剖析探究方向的基础上进行独立解题.教师在学生独立解题之后投影了学生解题中呈现的主要方法：寻找平面ABB1A1内与OH平行的直线共有三种方案；构造和平面ABB1A1平行且经过OH的平面一共有种方法（详细过程略）.

教师在课堂活动快要结束时又引导学生再次将视点回归到平行位置证明的关键点——线线平行的证明.

点评：学生在教师言简意赅的点拨与概括中很容易便产生了强烈的方法意识，科学、灵活运用方法进行解题来代替题海战术的思想逐步形成.

这是一节中心明确、重点突出、复习容量适中的复习课，通过各例题的探究以及方法的梳理使得各种平行的定义、判定、性质以及证明平行的通性通法都一一清晰地呈现，学生思维的踊跃也同时保障了本课的复习效果.

三、几点反思

教师在高三复习阶段应该以帮助学生构建清晰的知识体系为目标，在精选例题的基础上引导学生对解题的思路进行探究，并因此促成学生在开展积极思维活动的过程中掌握解题的通性通法，使得学生能够在具体的问题情境中将解题的思路与方法进行灵活的整合与运用，高三数学复习课堂教学只有达成这样的目标才能真正实现复习课的高效高质.蜻蜓点水或者狂轰滥炸式的复习往往只能使学生在认知的迷茫中似是而非，很多问题情境看似熟悉，但学生在真正自主构建解题思路或者探寻解题方法时又往往不得要领或者找不到突破口.为此，笔者认为在高三数学复习的过程中应该注重如下几点：

1.夯实双基

基础是发展之本、之源，尤其到了高三，我们不可忽视双基复习而片面地刷题，要将双基整合在具体的数学问题中，引导学生在处理数学问题时，完成知识、方法的有效复习，提升解决数学问题的能力和经验.虽然到了高三阶段，知识都是学生前面学习过的知识，但是学生仍然会出错，要帮助学生低空扫描，指导学生完成纠错夯实双基，与此同时提升解决数学问题的逻辑性、策略性.

2.培养思维严谨性

有很多学生到了高三学习数学越来越困难，什么原因？这部分学生往往有“会而不对，对而不全”的症结.究其原因是学生思维研究性不够，为此在高三复习的过程中应该引导学生多反思，反思解题过程是否周全、还有没有其他的注意点和解决问题的方法，通过不断地反思来提升学生对数学问题多视角的观察力.

3.开放的问题情境引领复习

开放性的情境更有利于发展学生的思维和解决数学问题的能力，因为开放学生往往可以与多个数学知识点、数学思想方法相联系，当然开放性问题不意味着难，让学生难以捉摸.笔者认为开放性问题的设置是为了符合所有学生思维发展需要的问题，其具有低起点、宽口径的特点.有助于调动班级全体学生主动地参与到问题解决中来，并能够具有更深层问题的生成，学生与教师的对话随着这些生成性问题而展开，学生科学严谨数学思维在复习过程中提升.

1.张幽婷.浅谈高三文科数学的复习教学［J］.中学数学教学参考，1994（3）.

2.张海江.高三数学复习策略［J］.考试与招生，2008（8）.