案例教学及其在中学数学课堂中的应用分析

☉江苏省梁丰高级中学 惠 静

一、案例教学理论基础

（一）案例教学的概念

案例教学法的基础就是案例，强调教与学两方面的共同参与，教学形式为针对案例或问题进行讨论，是一种合作化的新型教学方法.在这一方法中，学生是主体，教师是引导者，本质就是借由典型的事件，引导学生进行阅读、分析与讨论，形成自身的逻辑思维方法及思维方式，最终达到提高学生分析问题与解决问题能力、提升数学素养的目的.案例教学法最为明显的特征就是目的性、客观性、真实性、综合性、诱导性及实践性，因此广泛应用于中学数学教学中.

（二）案例教学的类型

案例教学这一模式根据案例在整堂课中所占的比重可以分为全程性和过程性两种案例教学方式.在全程案例教学模式中，案例贯穿整个课堂教学环节，而过程性案例教学模式与此不同，案例贯穿于课堂的部分环节.例如，在授课时，如果教师要求所有同学寻求案例的解决方案，进而完成本节课的所有教学目标，那么这种教学模式就是全程性案例教学；与此不同，如果教师在随堂练习环节就学生出现的典型错误进行点评，引导同学讨论，那么这种教学方式就是过程性案例教学.此外，根据案例数量，还可将案例教学分为单案例教学和多案例教学两种模式.

（三）案例教学的特性

1.参与性

案例教学法的核心理念就是要发挥学习者的主观能动性.因此，在该教学模式下，传统的师生角色发生了变化，教师起到引导和监督的作用，是讨论、互动的发起者与引导者，而不是传统的绝对控制者；学生也有别于过去的被动接受者，而是积极的参与者.这一点在案例呈现环节体现得较为明显，在讨论案例时，学生需要自行阅读教师给出的案例，认真分析，初步形成自己的分析过程和解决方案.在讨论环节，学生要积极发言，将自己的思考和判断展示出来.与传统的教学方法不同的是，在案例教学的过程中学生始终处于主动地位，不再是被动接受，体现了案例教学过程中学生的高参与性.

2.实践性

案例教学开展的基础就是案例，案例的作用就是促进学生学习，易于学生理解知识.在课堂上，教师的讲授只能传授知识，在这个过程中老师可以适当融入个人经验，却不能代替学生进行内化吸收，因此数学能力的提升离不开亲身实践，案例讨论就是实践活动的一种.所以，不依托案例，也就不存在案例教学了.在案例内容上，教师要保证其真实性、典型性、完整性及启发性；在叙述案例时，教师要突出案例的主要矛盾，引导学生探究案例背后的知识、原理，这样才能将课堂知识与现实生活有机结合，培养学生分析问题及解决问题的能力.

3.综合性

案例教学最主要的目标就是要依托于案例开展教学活动，提高学生独立思考、自主探索、发现问题、分析问题及解决问题的能力；与此同时，由于多数案例的内涵比较丰富，所以问题的答案往往不唯一，教师要引导学生探讨多种方法，在这个过程中让学生感受到实践活动的相对确定性及相对预期性；此外，案例的实施形式主要是辩论和讨论，在这个过程中学生的表达能力及辩论能力得到较大提升，同时也有助于学生打破“答案唯一”的思维定势，促进学生思维多元发展.

二、案例教学在中学数学课堂中的应用

（一）案例选择

案例教学的基础就是案例，因此案例的选择极为关键.一个好的课堂案例，既要能与课堂内容紧密结合，又要符合班级学生的总体认知水平与学习状况.比如，农村学校，教师选择的案例就要贴近农业及农村的生产生活；城市学校，选择的案例就需要贴近城市生活.只有这样，学生在接触到案例时才会感觉案例很贴近自己的生活，很好理解，讨论起来也有东西可说.以城市学校为例，在学习函数最值时，可以布置实践任务，让学生利用课余时间进入商场调查服装的打折促销活动.在学生调查完后，教师就选取某一个商场的促销活动为案例，让学生探究分析，综合考虑服装成本、折扣情况等因素，站在店家的角度，分析如何定价才能使得利润最大化.结合前期的调查，学生很容易就会确定问题的已知量、未知量和不同变量之间的等量关系，随后就能准确解决这一问题.

（二）讲授方法

案例教学这一模式与传统教学方法最大的区别就是强调了学生的主体地位及学生的主动性，因此在现实教学活动中，教师要改变过去应试教育中教师的绝对主导地位，逐步将课堂交还给学生.因此，在案例教学中，教师的角色从单一的知识传授者逐步变为学生学习的策划者、引导者、参与者及帮助者.与此同时，教学环节还要保证学生的积极性，因此教师就需要加强与学生的沟通与交流，及时了解学生学习的收获及存在的困难，帮助他们总结经验或克服困难，不仅起到老师的作用，还要成为学生的朋友，在必要时可以和学生互换角色，让学生去主导部分内容的教学.比如，在学习“立体几何”相关内容的时候，教师可以先安排学生组建小组，针对某一定理整理几何图形的应用案例，在这个过程中教师要起到监督和指导作用，避免学生走弯路.在课堂教学时，学生以小组为单位进行讲解.最后教师选出最合理、最为典型的案例，运用立体几何证明的相关理论解释这一案例，指导学生深入分析.

（三）学习方法

在传统的教学环节中，学生是被动的接受者，只能听老师讲课，机械地完成老师布置的任务，学习缺乏主动性.与此不同的是，在案例教学背景下，教学的中心变成了学生，教师的角色是案例演绎的组织者，可以理解成“导演”.案例教学就是教师引导学生发挥主观能动性，积极地开展学习与探究活动，进而实现自我发展的最大化.单纯依靠教师讲解课本知识，教学生怎么做，就变成了越俎代庖，学生的能力很难得到提升.因此，教师需要关注学生学习能力的提升，强调学生学习的积极性与主动性，同时也要注重学生的探究意识、合作意识及创新意识等的培养.

三、教学实例分析——以苏教版必修3《算法初步》为例

（一）案例导入

古今中外，许多人致力于圆周率的研究与计算.为了计算出圆周率的越来越好的近似值，一代代的数学家为这个神秘的数贡献了无数的时间与心血.我国东汉的数学家刘徽利用“割圆术”计算圆的面积及圆周率.“割圆术”被称为千古绝技，它的原理是用圆内接正多边形的面积去逼近圆的面积，具体计算如下：在单位圆内作内接正六边形，其面积记为A1，边长记为a1，在此基础上作圆内接正12边形，面积记为A2，边长为a2，……一直做下去，记该圆的内接正6×2n-1边形的面积为An，边长为an.由于所考虑的是单位圆，计算出的An即为圆周率π的近似值，n越大，An与π越接近.

（二）思路探讨

应首先推导出an，an-1，An，An-1的关系.如图1，设PQ为圆内接正6×2n-1边形的一边，即PQ=an-1，OR为与PQ垂直的半径，R为弧PQ的中点，显然PR=an.

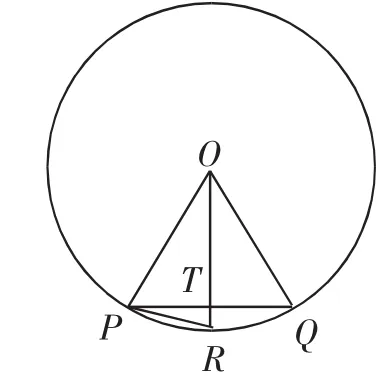
图1

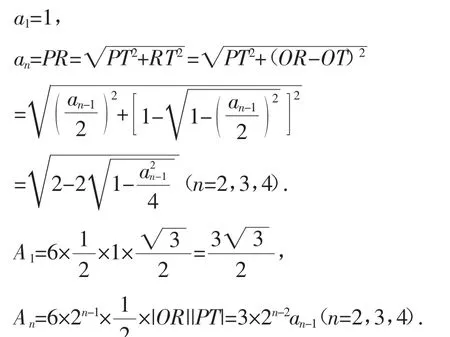
（三）结论演绎

通过上面两式，从a1=1开始进行迭代，可逐步计算出an与An.由于所考虑的是单位圆，计算出的An即为圆周率π的近似值，n越大，An与π越接近.算法和流程图（图2）如下：

Begin

Read n

1←a

For ifrom 2 to n

A←3×2i-2×a

a←Sqrt［2-2×Sqrt［1-a2/4］］；

Printi，A，a

End for

End

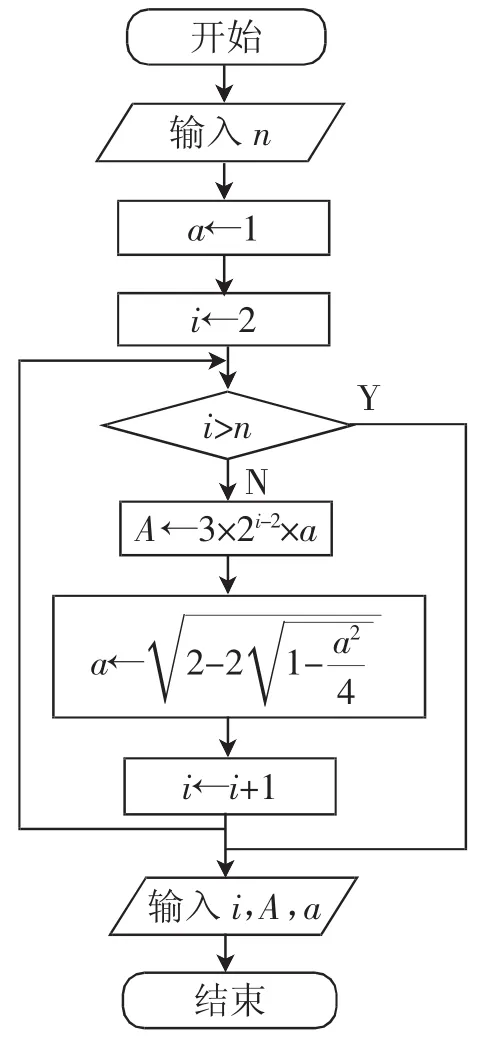
图2

（四）数学素养剖析

1.数形结合思想

数形结合思想指的就是利用几何图形来处理代数问题，使得题目的数量关系更为直观地反映出来，将数字与图形巧妙地结合起来，在此基础上寻求解题思路，简化问题的解决过程.上述案例在解决时，将圆周率这一代数内容和几何图形结合起来，通过圆内接正多边形的面积去逼近圆的面积，进而去探究圆周率的值，使得代数问题的解决过程更为直观，也更为简单.

2.归纳总结思想

在苏教版高中数学中，归纳总结是重要的思想方法，其内核就是寻找规律，比如排列组合、概率、数列等内容的学习都会用到这种思想方法.上述案例不断地利用圆内接正多边形的面积去逼近圆的面积，一步步迭代，一步步总结，最终发现其中的数学关系，得出圆周率的取值区间.

四、结束语

案例教学法的产生是各级教育工作者及教学管理单位对新课改要求的积极响应，是新形式背景下对传统教学方法的有效改进，能够较好地弱化传统应试教育思想的影响，同时也能创新教学思路，完善教学体系.但是，我们要清醒地认识到案例教学法不是一成不变的，需要教育工作者依托实际，结合学生、学校的具体情况，有针对性地开展.如果一味地照搬照抄，那么案例教学只能流于形式，效果甚微.具体到高中数学教学，教师需要从实际出发，了解学校的发展定位及学生的学习状况，既要提升自身综合素质，又要选择适合本班学生的案例，科学地将这种方法融入到现行的教学环节，真正地构建高效课堂.F