大陆和台湾高中数学教材中数学文化内容的比较研究——以“统计与概率”内容为例

☉首都师范大学数学科学学院 覃 淋

2003年颁布的《普通高中数学课程标准（实验）》将“体现数学的文化价值”作为高中数学课程的基本理念之一，并进一步明确说明，“数学是人类文化的重要组成部分……数学课程应帮助学生了解数学在人类文明发展中的作用，帮助学生形成正确的数学观”.［1］还提出了对“数学文化”的学习要求，设立了“数学史选讲”的专题，要求学生通过高中阶段数学的学习，能够了解数学科学在人类社会发展中的作用，领会数学的人文价值、美学价值.在“教材编写建议”中指出，教材编写应将数学的文化价值渗透到各部分内容中.那么，高中数学教材中文化价值表现在哪些方面？文化材料的运用方式及水平如何？本文以高中数学教材中“统计与概率”内容为例，比较大陆和台湾教材中的数学文化内容及其运用水平，了解大陆和台湾高中数学教材中数学文化内容渗透的共性和差异，希望能为我国高中数学教材“统计与概率”内容的编写提供一些建议.

一、研究对象

考虑教材的使用范围及教材是否能体现所在地区课程标准的理念，再结合教材的出版时间，最后确定了表1中所列数学教材［2～5］.

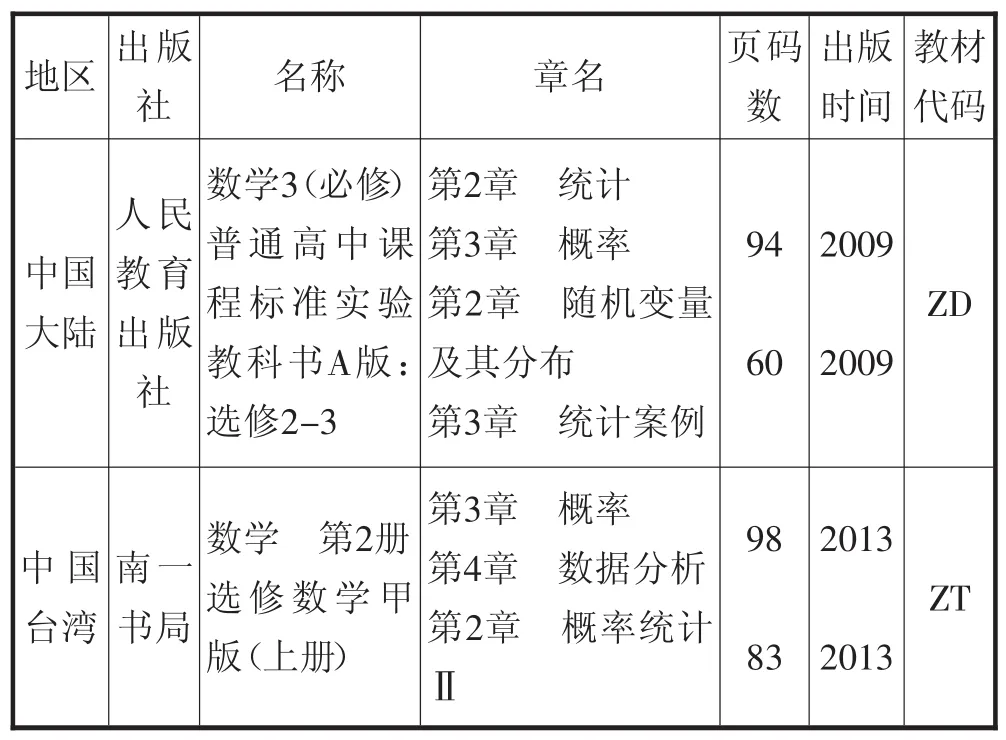
表1 教材样本及基本信息

二、数学文化内涵的界定及其运用方式

数学文化是一个涉及范围很广的名称，其内涵至今并无统一的界定，不同的学者从不同的角度有不同的看法.可以说，凡是与数学有关的一切事物都可以归为数学文化的范畴.这里我们采用顾沛教授的观点，“数学文化”的内涵，“简单地说，是指数学的思想、精神、方法、观点，以及它们的形成和发展；广泛地说，除上述内涵之外，还包含数学家、数学史、数学美、数学教育、数学发展中的人文成分、数学与社会的联系、数学与各种文化的联系，等等”.［6］

因此，本文所指的数学文化是广义的，包括：数学史、数学与生活、数学与人文、数学与艺术、数学与科学，但不涉及数学思想、数学方法等.为叙述方便，我们将数学与生活、数学与人文、数学与艺术和数学与科学等数学文化内容统称为其他数学文化，也就是说，本文中的数学文化包括数学史和其他数学文化两大类.

（一）教材中数学史料的运用方式及其运用水平

在数学教材中运用数学史料，有较为悠久的历史.早在20世纪初的一些数学教材中，已经开始大量运用数学史材料于教材中，只是大多以数学故事的形式出现，与教学内容关系不是特别密切.一般而言，教材中数学史料的呈现方式可分为显性和隐性两大类.如数学家画像、数学家的传记、数学概念起源的介绍、数学符号的历史、数学家的故事、历史数学名题等，都属于显性方式.显性数学史料的主要作用是引起学生的学习兴趣，激发学习动机.隐性方式则是根据实际教学，对数学史料进行改编、重构，保留历史上相关数学概念发生发展的关键步骤，以润物无声的方式体现数学史料提供的思想和方法，所谓的“发生教学法”就属于隐性方式.在隐性呈现方式中，数学史料的表现并不十分明显，很多时候隐藏于一些数学概念、数学命题或例题习题之中，按数学知识发生发展的顺序展现相关数学内容，让学生在无意识中经历数学的“再创造”的过程.

关于教材中数学史料运用方式的分类，到目前为止，得到大家广泛认可的分类方式还没有.本文采用华东师大汪晓勤教授建立的分析框架［7］，见表2.该分类框架是按数学史与数学知识的关联程度，将教材中运用数学史料的方式分为5类：点缀式、附加式、复制式、顺应式、重构式.若按数学史料的呈现方式看，前三种属于显性，后两种属于隐性方式.

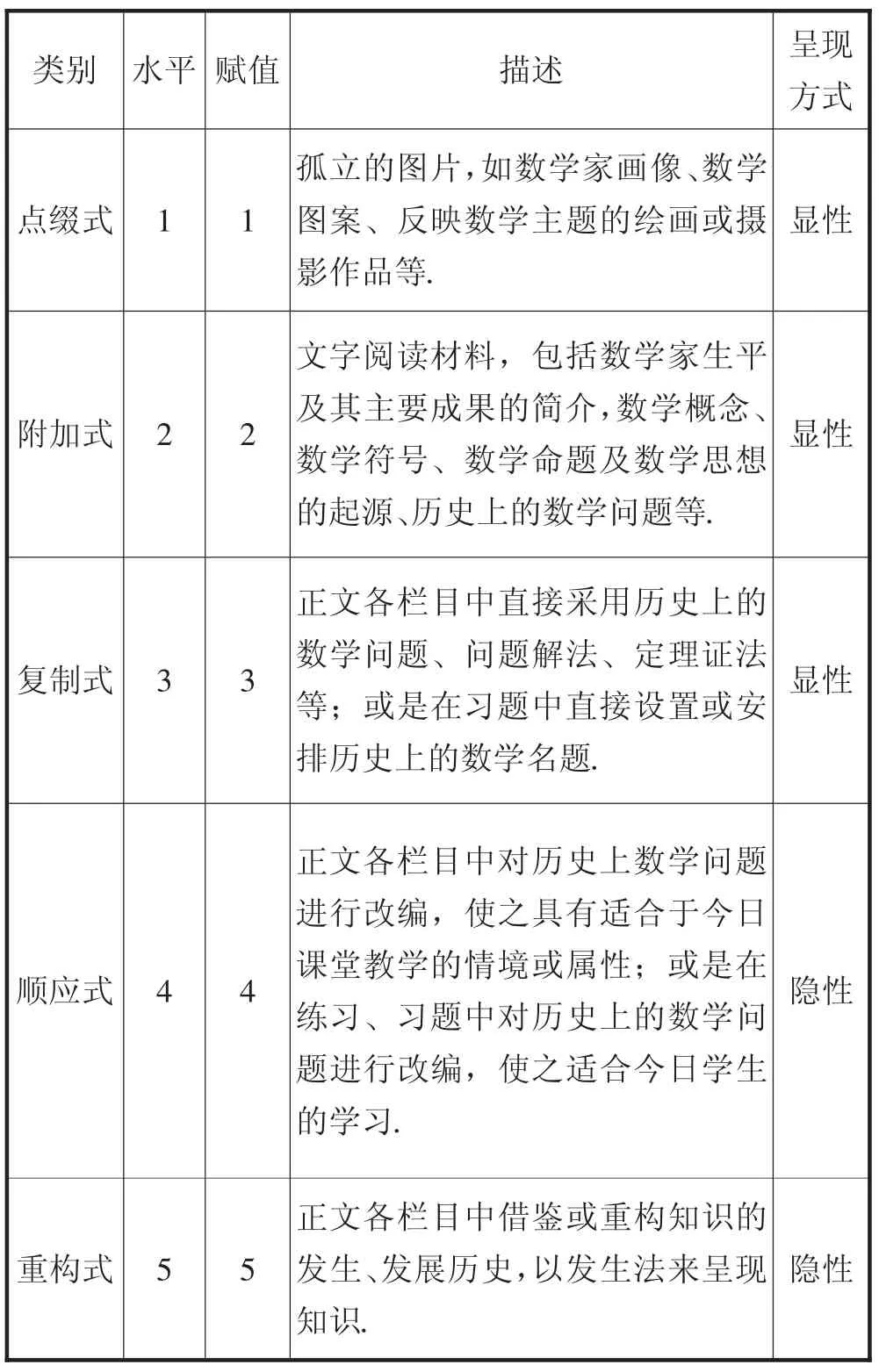
表2 数学教材中运用数学史料的五种方式及水平

对于教材中数学史料的运用水平，采用如下的计算方法［7］：首先，按数学史料的运用水平赋值，即水平1（点缀式）赋值为1，水平2（附加式）赋值为2，以此类推.其次，利用如下公式计算教材运用数学史料的水平A=

其中，Ai表示所处水平i的数学史料的数量，Bi表示数学史料所处水平的赋值，即Bi=i，n表示教材中数学史料的总数.利用此公式，可以对不同版本教材，或是同一版本教材中不同册次教材，或是不同版本教材中某一内容运用数学史料的水平进行量化处理.

（二）其他数学文化内容及运用方式

根据上面的约定，其他数学文化内容包括：数学与生活、数学与人文、数学与艺术和数学与科学，下面分别加以阐述.

1.数学与生活

借鉴PISA（2015）对数学问题背景的分类［8］，本文根据现实生活中的数学文化与学生的关联程度，将数学与生活分为个人生活、公共生活两类.具体如表3.

表3 数学与生活的分类

2.数学与人文、艺术、科学

根据教材所呈现的内容，将数学与人文内容界定为：文学、戏剧、历史等.将数学与艺术的内容界定为：美术、音乐、电影、舞蹈等.根据科学研究的对象，将数学与科学的内容分为：地球科学、生命科学、物质科学；其中地球科学包括地理、天文、环境、自然资源、灾害、气象等，生命科学包括生物学、医学、农业、健康、食品等，物质科学包括物理、化学、计算机、工业技术等.具体如表4.

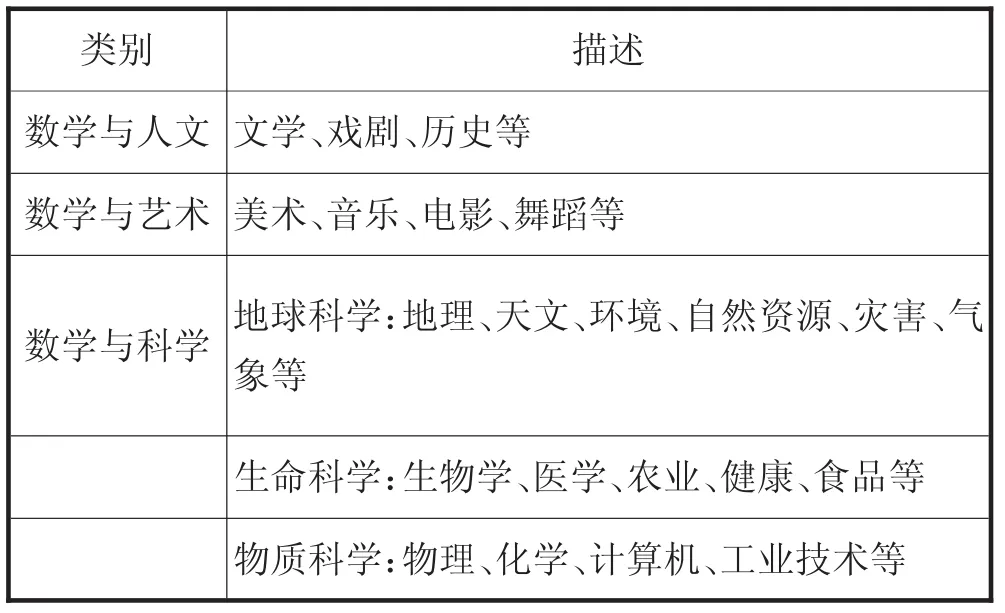
表4 数学与人文、艺术、科学的分类

3.其他数学文化内容的运用方式

de Lange根据背景与数学问题的关联程度将背景分为［9］：（1）无背景；（2）掩饰数学问题；（3）数学问题的有机组成部分.本文在此基础上，根据数学文化与数学知识的关联程度，将其他数学文化内容的运用方式分为两类：附加型和顺应型.具体如表5.

表5 其他数学文化内容的运用方式

三、结果

按照上述对数学文化内容的分类，对两套教材在数学史、数学与生活（下面简称生活）、数学与人文、数学与艺术、数学与科学（下面简称科学）方面出现的次数与百分比进行统计，得到的结果如图1、图2.可能是研究的内容的缘故，两套教材中数学文化内容涉及人文、艺术非常之少.考虑到这种情况，我们将数学与人文、数学与艺术这两个数学文化内容的子类合并到一起，统称为数学与艺术（下面简称艺术）.

由图1知，两套教材在数学史、数学与生活、数学与艺术、数学与科学四个方面有大致相同的趋势，都呈斜“N”字型，两套教材都是在数学史、艺术、科学三个方面的数学文化内容很少，而在数学与生活方面内容最多.这在图2中表现非常明显，这也说明在两套教材中数学文化集中体现在现实生活方面.为更清楚的比较两套教材在各个数学文化内容上的差异与共性，下面从每个维度来进一步详细说明.

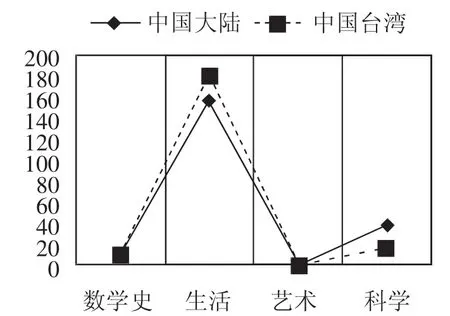
图1 两套教材数学文化内容折线图

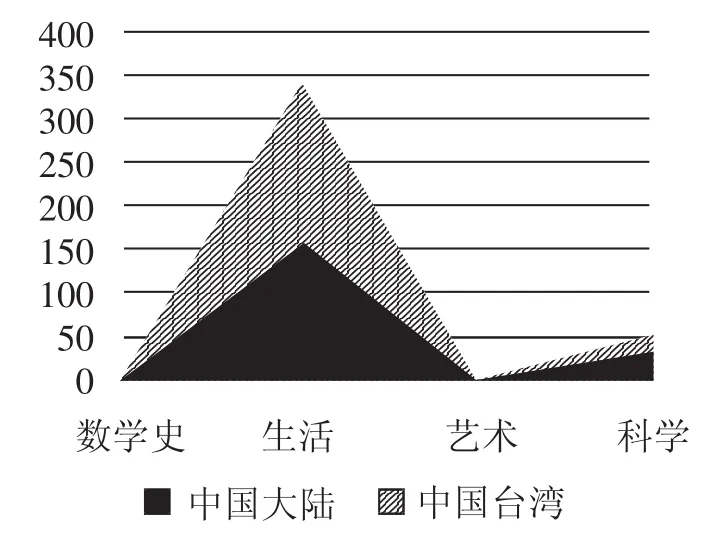
图2 两套教材数学文化内容面积图

1.在数学史方面的特点

两套教材中涉及数学史料方面的内容都比较少，大陆教材共有6处，台湾教材共11处.两套教材中数学史料的呈现方式以显性为主，其中仅有一处运用了“顺应式”的方式，大陆教材在引入概率的“统计定义”时，利用了历史上数学家掷硬币的试验结果来说明：对任意给定的随机事件，随着试验次数的增加，事件A发生的频率fn（A）稳定于概率P（A），因此我们可以用频率来估计概率［2］.

大陆教材在“统计与概率”部分涉及的数学史料包括：“回归”一词的起源、含义及其发展，概率的“统计定义”、数学家雅各布·伯努利（Jacob Bernoulli，1654-1705）的介绍及大数定律、蒙特卡罗方法、伯努利试验、正态分布（高斯分布）名称的来源.台湾教材中涉及的数学史料有：费马（Pierre de Fermat，1601-1665）的画像、概率论的起源、拉普拉斯（Pierre-Simon Laplace，1749-1827）的画像、概率的“古典定义”、贝叶斯（Thomas Bayes，1702-1761）的画像、贝叶斯学派、“辛普生诡辩”问题、伯努利试验、棣·莫弗（Abraham de Moivre，1667-1754）及高斯（Gauss，1777-1855）的画像、正态分布（高斯分布）名称的来源.

两套教材中数学史料出现的位置大都在正文中，只有台湾教材在课后习题中采用了“辛普生诡辩”问题.对两套教材中数学史料的运用方式进行具体分析，发现两套教材大都以“附加式”的方式运用数学史料，处于较低水平，以发生法来呈现数学知识的“重构式”均未涉及（具体见表6）.值得注意的是，台湾教材中有大量的数学家的画像，以点缀的方式来体现数学的文化价值，大陆教材则没有采用此方式，而是在教材正文以“旁白”的形式对一些与教材知识有关的材料进行简单介绍，如上面提到的“回归”一词的起源及发展，蒙特卡罗方法等内容.

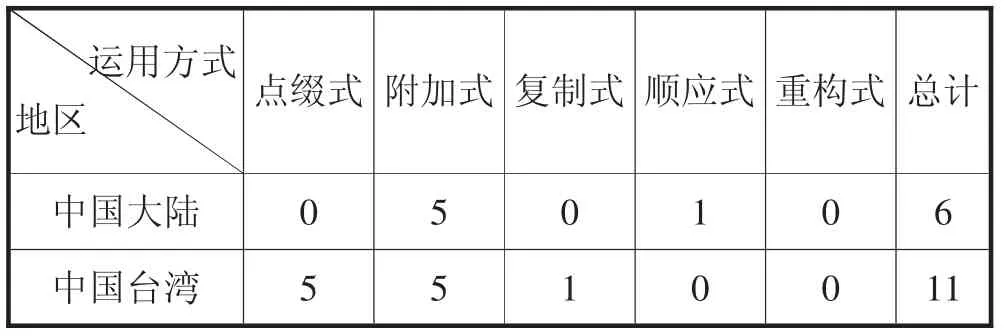
表6 两套教材数学史料运用方式

根据前面提到的教材中数学史料的运用水平的计算公式，我们可以计算出大陆教材中“统计与概率”内容数学史料的运用水平同样，可以计算得到台湾教材中“统计与概率”内容数学史料的运用水平为ZT=1.64.可以看出，在“统计与概率”部分，大陆高中数学教材数学史料的运用水平高于台湾高中数学教材.同时表明，教材中数学史料的数量与数学史料的运用水平之间并无直接的联系.

2.在其他数学文化方面的特点

由上面的图1知，两套教材在其他数学文化内容主要集中在“数学与生活”方面，在“数学与艺术”方面，两套教材所涉及的可以忽略不计.

（1）在数学与生活方面

按照子类和运用方式分别进行统计，得到表7.可以发现，两套教材都有较多的内容与生活紧密联系，台湾教材在与生活相关的内容出现的次数大于大陆教材.按子类划分来看，两套教材在与学生个人生活相关的内容，数量上相差不是很大，比例上大陆教材大于台湾教材.台湾教材与生活有关的内容主要集中在“公共生活”，大陆和台湾教材各自所占比例分别为73.3%、81%.这说明，大陆教材比台湾教材更加贴近学生的个人生活.而从两套教材所涉及的内容来看，在个人生活方面，两套教材涉及的内容大都是学生的考试成绩、身高、体重等内容，范围比较狭窄；在公共生活方面，内容则比较丰富，涉及运动（篮球比赛、足球比赛、射击、田径）、交通、游戏（掷硬币、掷骰子、袋中摸球）、职业等.

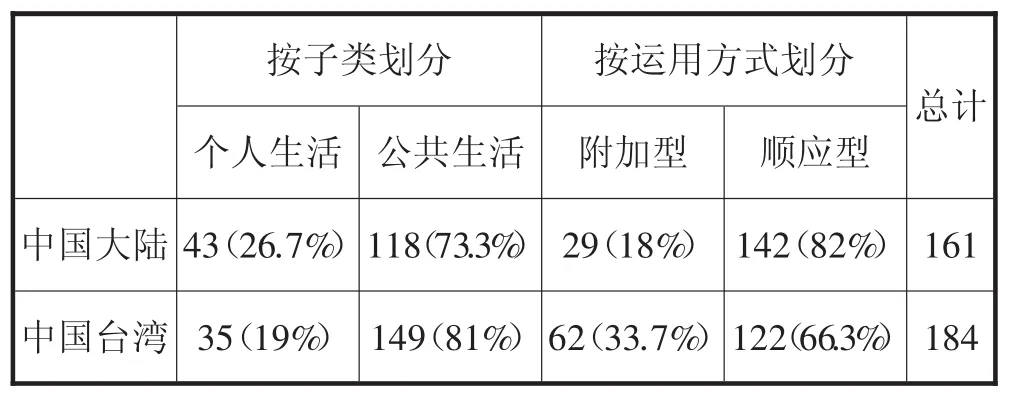
表7 两套教材数学与生活的水平分类

由表7可知，在“数学与生活”内容中，两套教材大多是顺应型，即生活背景与数学知识不可分离.这可能和本文所研究的对象有关，“统计与概率”相对于传统的中学数学教学内容（如代数、几何）而言，与生活的练习较为密切.如大陆教材中给出的多个阅读材料，“一个著名的案例”、“广告数据的可靠性”等，都说明了“统计与概率”在生活中有较为广泛的应用.

同时，我们还发现，在“数学与生活”这一数学文化内容中，统计、概率部分有着比较显著的区别，这一点在后面会进一步论述.

（2）在数学与科学方面

统计表明，两套教材在“数学与科学”方面较为薄弱.大陆教材共有39处，台湾教材仅有17处，并且超过一半的内容都是附加型的，即与教材内容可分离，去掉也不会影响学生正常的数学知识的学习.

此外，在这一内容中，大陆教材的内容多与气象、生物学有关，台湾教材则多与工业生产相关；两套教材在与其他学科的交叉联系上较为薄弱.

3.教材中统计、概率二者在数学文化渗透方面的差别

在数学史料中，大陆教材仅有1处属于统计的内容，其余5处均是涉及概率的.台湾教材中也仅有3处内容是关于统计的，另外8处都出现在概率内容中.这说明两套教材都重视概率超过统计.

在“数学与生活”的内容中，如表8所示.这一内容中，统计、概率的差别非常显著.两套教材中，概率部分涉及生活的内容都接近统计中与生活相关的内容的两倍.从数学与生活方面的呈现方式来看，大陆教材在附加型的呈现方式中，统计与概率二者相差不大，台湾教材相差则比较大.在顺应型的呈现方式中，两套教材“统计”与“概率”的差别都比较大，概率部分显著高于统计部分；台湾教材的差别更为明显，概率部分达到了统计部分的4倍.

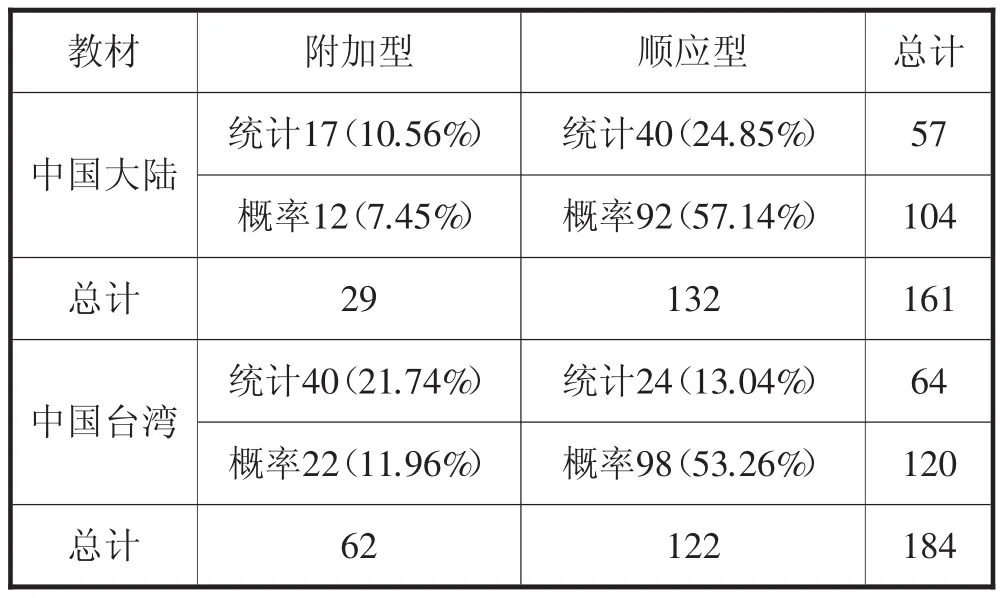
表8 两套教材统计、概率二者在“生活”方面的差别

四、结论及建议

从数学文化内容在两套教材中出现的范围、次数及运用水平来看，应该说两套教材的编写者都比较重视数学文化的渗透.但通过对教材中文化材料的运用水平的分析，发现它们与将数学文化和数学课程内容有机结合的目标还存在一定的差距.为使教材中的数学文化内容更好的促进学生对数学知识的学习，教材中融入数学文化内容的数量及运用水平上都有待改进.

1.融入更多的数学史料

数学史料的融入是数学文化的主要体现之一，但是两套教材涉及的数学史料都很少，数学史料的运用水平也较为粗浅.大多以点缀式、附加式的方式对数学概念、符号的起源，数学家生平，历史上的数学问题等进行简单的介绍.如大陆教材在“旁白”中介绍了“回归”一词的来源，是高尔顿（Francils Galton，1822-1911）在研究祖先与后代身高之间的关系时引进的，还以“旁白”的方式简要介绍了“蒙特卡罗”方法的兴起与发展.很显然，这种数学史料虽与教学内容相关，但很难引起学生的兴趣，在课堂上教师一般也会选择性的忽视.

可以说，数学教材中融入数学史料，是数学文化内容的直接反映.了解概率论历史都知道，现代的概率理论开始于帕斯卡与费马的通信.进一步考察概率论的历史可以发现，历史上很多材料都可用于今日的课堂教学.

以卡尔达诺（Girolamo Cardano，1501-1576）的著作《论机会游戏》（1526）为例，该书中讨论了德·默勒曾经向帕斯卡（Blaise Pascal，1623-1662）提出的问题，“掷一对骰子多少次才能使出现两个6点的机会达到50%”.卡尔达诺给出了自己的答案，不过遗憾的是，他给出的答案是错误的.这一问题也被意大利数学家帕乔利（Luca Pacioli，1445-1517）讨论过，在其著作《算术、几何、比和比例集成》（1494）有这样一个问题，“甲、乙两人进行一场公平的游戏，约定先胜6局者胜.实际上在家赢了5局，乙赢了3局后，游戏中断.请问赌金该如何分配？”帕乔利认为赌金应按照5∶3的比例分配，这显然是一个错误的答案.

另一位意大利数学家塔尔塔利亚（NicccoloTartaglia，1499-1557）也讨论过此问题.在其著作《论数字与度量》（1556）中，他指出了帕乔利的答案是错误的.“因为两个得分相差两局，甲需要赢的次数仅是乙的，甲应该拿走乙赌注份额的”，所以赌金应该按2∶1来分配，但他对自己的答案是否正确也没有信心.因此，在书中有这样一句话，“这样一个问题的解决是法律上的而非数学上的，所以无论怎样分配都有理由上诉.”［10］今天我们已经知道，他的说法也是错误的.

这些问题显然比今天课本中的问题有趣得多，为什么不对它们进行改编或重构，然后编入教材呢？让学生去解一些早期数学家感兴趣的问题，可以让学生回到问题提出的时候；一个问题研究的原因、最早的解法是什么、最后的解法是什么、最好的解法又是什么，都能激发学生的兴趣；并且学生在解决这些问题后，会获得某种程度上的成就感.

2.注重数学与其他学科的联系

数学的思想和方法已经渗透到社会的方方面面，统计与概率是数学中应用性较强的分支，其应用范围已经涉及整个自然科学、社会科学、工程计算、管理、经济和文学领域.通过对两套教材中数学文化内容的统计，发现两套教材在数学与科学、数学与艺术、数学与人文等方面都有待加强.

数学来源于现实，存在于现实，并应用于现实.现实的数学不仅仅是算术、几何、代数、统计等数学内容的相互交织，还联系着物理、化学、生物等自然科学和一些人文学科，这些学科中许多材料都可作为“统计与概率”教学的素材.

在数学与生活方面，也应进一步增加与学生个人生活相关的内容.对于数学的学习，不仅要与其他学科联系，还要考虑与现实世界的联系.“统计与概率”作为数学中应用性较强的内容，更应该联系学生的实际生活来促进学生的数学学习，加强学生应用数学的意识，这样学生才有可能利用所学数学知识去分析和解决实际问题.

3.数学文化内容的运用水平有待提高

从整体上看，两套教材在数学文化内容的运用水平都比较低，尤其是在数学史料的运用上，数学史料的运用大都以显性方式.在数学与生活方面，数学文化的呈现方式主要是顺应型，与问题结合较为紧密.在这一点上，大陆教材做得比台湾教材好.但是，我们也应看到的是，两套教材中与学生个人生活相关的内容都比较少.而在数学与科学、数学与人文、数学与艺术等方面，数学文化内容的数量都有待增加，运用水平也有待提高.

1.中华人民共和国教育部.普通高中数学课程标准（实验）［M］.北京：人民教育出版社，2003.

2.课程教材研究所，中学数学课程教材研发中心.普通高中课程标准实验教科书A版数学（必修3）［M］.北京：人民教育出版社，2009.

3.课程教材研究所，中学数学课程教材研发中心.普通高中课程标准实验教科书A版数学（选修2-3）［M］.北京：人民教育出版社，2009.

4.林福来.普通高级中学数学（第二册）［M］.台南：南一书局，2013.

5.林福来.普通高级中学选修数学甲版（上册）［M］.台南：南一书局，2013.

6.顾沛.数学文化［M］.北京：高等教育出版社，2008.

7.覃淋.台湾初中数学教材中的数学史［J］.中学数学杂志，2017，（8）：33-37.

8.OECD.PISA 2015draftmathematicsframework［EB/OL］.http：//www.oecd.org/pisa /pisaproducts /pisa2015draftframeworks.htm，2017.9.20.

9.de Lange.Assessment：No Change without Problems［A］.In：Romberg TA.Reform in School Mathematics and Authentic Assessment［C］.New York：SUNY Press，1995.

10.卡茨.数学史通论［M］.北京：高等教育出版社，2004.