回归 变式 提升
——以“函数复习”为例谈高三数学课教学策略
☉江苏省常熟市尚湖高级中学 马怡平
高三数学复习课遵循课程计划标准而不得随意增减课时,因此,提升高三数学复习课的效率是高三总复习阶段尤其重要的问题.下面以笔者听到的一节高三函数复习课为例,就该节课带给了我们的启迪、思考和示范谈几点笔者的思考.
一、在回归课本的基础上紧抓主干、构建网络
该老师在课的一开始就向学生提出了问题:回忆高一学期以及近期复习的函数内容,你们对函数主要内容、方法以及知识结构方面有体会吗?紧接着,该老师引导学生从函数的结构功能这一角度重新认识了函数的核心内容.然后展示课前设计的四道小题让学生在练习中加深对函数核心内容的感悟.
(1)某市收取居民月用水时采用了如图1所示的阶梯式收费法,李铭家今年1月用水量为14吨,应付_______元水费.
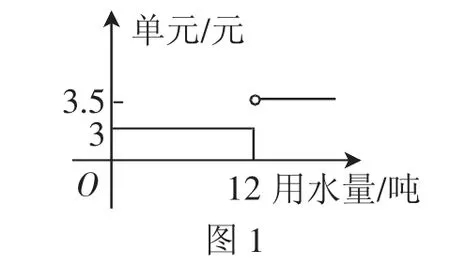
(2)已知直线x=a,定义域为[0,6]的函数y=(fx),两图像有______个交点.
(4)已知函数f(x)=sin4x,将其图像向左平移至少______个单位后,该函数为偶函数.
从以上4个小题不难看出,函数题的求解应多多利用数形结合的方法,但定义域问题是作图时应该要注意的.
评析:(1)高三数学复习课往往会在知识点的梳理上下功夫,这样的复习虽然对学生知识网络结构的建构极有好处,但耗时多且学生相对被动也是如此复习可能存在的弊端.但该老师的这节课让学生在知识的自我回顾与复习中抓住了知识的主干与结构本质,学生在自主整理知识要点与重点的同时也张扬了个性.学生在“由薄到厚”的读书中最终实现了“由厚到薄”、纲举目张的过程转变.
(2)该老师安排的这4小题虽然起点低,但却具有函数习题的典型性且各有侧重.文字语言和图像语言之间的转译和表达是第1小题练习的侧重点;加强函数概念的理解是第2小题练习的侧重点;提升学生数学阅读与认知能力是第3小题练习的侧重点;加强学生对函数图像特征的理解与把握是第4小题练习的侧重点.这4个小题的解决使得学生对函数部分的系统结构和本质特征产生了更深的体会和感悟.
(3)第4小题是该老师借班上课了解学生学情之后临时添加的,这一行为及时且果断,学生在函数与最近所学内容的结合学练中焕发出了更强的积极性.
(4)该老师面对这样几道填空题也坚持让学生上黑板板书,这样的举动对于学生解题的规范性、逻辑性以及简洁性是极有好处的,很多说不清道不明的东西也在板书中得到了更好的体现,学生对解题的评价、纠错等也会更加直观,对题目本质加深理解的同时正是学生知识内化的过程.
二、在变式中揭示方法、渗透思想
虽然夯实基础与基本方法是高三复习时的主旋律,但停留在这些基本点上的做法也是不妥当的.《考试大纲》明确提出了命题应着眼于知识网络交汇点的具体要求.因此,高三数学教师应该树立知识“交汇点”的运用意识,并因此制定出有针对性的教学举措来应对着眼于知识交汇点的各个命题.因此,该老师也有了以下设计:
例1 对∀x∈[1,3],不等式x2+2x+m≥0都成立,求m的取值范围.
将学生的回答进行归纳后得出以下解题思路:①二次函数图像法;②利用单调性解题;③分离参数法.解决恒成立问题的一般方法也因此得以归纳出来.
该老师在学生解题的基础上对方法③作进一步的分析与探讨,把参数m分离,要使不等式在[1,3]上恒成立,转化成m≥-(x2+2x)在[1,3]恒成立,故求出函数f(x)=-x2-2x在[1,3]上的最大值即可.而f(x)=-x2-2x在[1,3]上的最值可以利用函数单调性或图像可以求解.因此,上题可变式为:∃x∈[1,3],使不等式x2+2x+m≥0成立,求m的取值范围.同时又提出问题:
问题1:这两题有不同的地方吗?
问题2:若将以上不等式转化成m≥-(x2+2x),满足条件的m的范围应该如何去求呢?
问题1的答案是明显的.学生经过一定的思考也很快得出了问题2的答案,对∃x∈[1,3],求出函数f(x)=-x2-2x在[1,3]上的最小值就可以了.
少数学生已经能够理解、掌握恒成立和存在性问题之间的区分了,但该老师并不满足于此,继续提问:我们班同学中最大与最小年龄分别是20岁和17岁,现在,年龄x满足①m≥x成立,其中满足条件的m的范围应该如何去求呢?②存在x,使m≥x,满足条件的m的范围应该如何去求呢?学生在熟悉的背景中学习顿感轻松.
该老师紧接着又进行了变式:
若∃x∈[1,3],且令x2+2x+m≥0成立,则m的取值范围如何?
思考方法跟上题相比是类似的,关键是求出f(x)=x2+2x在[1,3]上的最值.
追问:若是填空题,如何才能尽快求出f(x)=x2+2x的最值?若是解答题,又应该如何去求f(x)的最值.
学生经过简短的思考很快便产生了小题运用复合函数的单调性、解答题运用求导或单调性定义来解决问题这一答案.该老师在学生的思维上进行了板书以规范学生的解题过程.
从以上题组的练习与分析可以得出研究函数问题的基本点是其单调性,而函数问题研究与解决的交汇点则是不等式与导数等知识的交汇.涉及参数的函数问题则应该首先将参数分离并转化.
评析:在知识网络的交汇点处进行例题的设计并进行变式,所有的问题经过比较与辨析都转化成了函数问题的核心内容——单调性问题,数形结合等数学思想在这样利于总结的比较与分析中得以渗透,教学的近期与远期目标也更加和谐与统一.
三、通过解题策略的指导促进学生能力提升
立足基本点、形成交汇点并最终抵达制高点的高考数学复习往往还需要直觉、估算、转换视角等思维方式参与才能取得最为完美的效果.
例2已知奇函数f(x)是R上的单调增函数,数列{an}是等差数列,且a2>0,试证明:f(a1)+f(a2)+f(a3)>0.
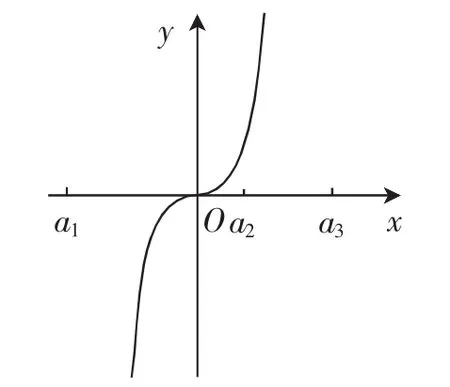
图2
分析:(1)采取具体例子或图像来降低解题抽象度;(2)化整为零,局部解决.
证明:因为a2>0,而f(x)是在R上的增函数,所以f(a2)>f(0),而f(x)是在R上的奇函数,故f(0)=0,所以f(a2)>f(0)=0.又因为{an}是等差数列,故2a2=a1+a3>0,所以a1>-a3,所以f(a1)>f(-a3)=-f(a3),即f(a1)+f(a3)>0,从而f(a1)+f(a2)+f(a3)>0.
利用直观图像得到f(a2)>0是本题得以求解的关键,一旦将问题转化成f(a2)>0的证明,那么此题的突破口完全展现了.
根据本例我们可以知道,数形结合的思想方法在函数性质的研究中往往能使学生在直观的图像中轻松找到问题解决的突破口.
不过,课堂教学活动到这个时候并没有结束,“变更命题后将会产生哪些新问题”是该老师抛出的又一启发学生思考的问题.
学生在该老师的启发下又从原命题、逆命题、否命题等各个角度尝试进行命题的变更,这一连串的新命题正是该老师留给学生课后思考、讨论、证明的作业.
评析:(1)该老师通过背景介绍与解题策略指导将一道比较有难度的例题放在了师生互动交流讨论中,学生的思维方式在这个过程中得到了很好的优化,教育功能一目了然.(2)变更命题后产生哪些新问题的追问使得例题更具开放性和拓展性,课堂活动即将结束阶段的思维高潮令学生往往意犹未尽,学生对解题步骤的完善往往产生更大动力.
这是一堂从基本点着手教学的案例分析课,学生在教师的引导中学会了归纳数学思想与方法.例题的变更也使得学生在分析问题、变更问题以及解决问题的过程中不时经历思维的冲浪,学生在意犹未尽的思维海洋中不断加深对知识的探究与巩固,课堂效率不同凡响.

