求几类数列公共项问题的解题策略

唐春婷

（上海市民办远东学校〈普通高中〉）

一、两个等差数列的公共项问题

解一：为了发现公共项的规律，不妨将两个数列分别列举出一些项：

5，8，11，14，17，20，23，26，29，32，35，38，41…

3，7，11，15，19，23，27，31，35，39，43，47，51…

显然相同的项构成的数列是11，23，35，47…

由以上分析可知，相同项构成以c1=11为首项，以d=12为公差的等差数列，通项公式为cn=12n-1。

bp+1=4（p+1）-1=4p+3=3m+6=3（m+2）∉ ｛an｝；

bp+2=4（p+2）-1=4p+7=3m+10=3（m+3）+1∉ ｛an｝；

bp+3=4（p+3）-1=4p+11=3m+14=3（m+4）+2∈ ｛an｝；

所以，cn+1=bp+3，cn=bp。

cn+1-cn=bp+3-bp=12，易得公共项构成以c1=11为首项，以d=12为公差的等差数列，通项公式为cn=12n-1。

点评：由此可以看出新数列的公差应是原来两数列的公差的最小公倍数。对于解一，推理不够严谨，但是对于解选择填空题，也不失为一种快速的方法。解二的推理较为严谨，技巧性较强，下面我们用中国剩余定理探究一下问题的本源。

解三：显然数列 ｛an｝的每一项是被3除余2（也可以说被3除余-1）的自然数，数列 ｛bn｝的每一项是被4除余-1的自然数，这样两个数列的每一项余数相同，设构成的新数列为 ｛cn｝，根据同余，则 ｛cn｝满足易得cn=12k-1，又通过简单的计算得新数列的首项为11，因此令k=n，k∈z所以cn=12n-1。

对于三个或者三个以上等差数列，要求它们的公共项从小到大排成的新数列的通项公式，同样可以用到中国剩余定理，转化为有关同余的问题，关键先求出数列公差的最小公倍数。如假设p个等差数列 ｛ani｝，i=1，2，…，p 的通项公式分别为 an1=e1n+f1，an2=e2n+f2，…，anp=epn+fp，公差 e1，e2，…，ep全不为 0，则这 p 个等差数列的公共项按从小到大的顺序组成一个新的等差数列 ｛cn｝，新数列公差d即为的最小公倍数，而新数列的首项通过简单的计算得出。

二、等差数列与等比数列的公共项问题

例：等差数列an=4n-1，等比数列bn=3n，它们的公共项由小到大排成新的数列 ｛cn｝，求 ｛cn｝的通项公式。

解一：设等差数列 ｛an｝的第m项与等比数列 ｛bn｝的第p项相等，即 cn=am=bp，即 cn=4m-1=3p，bp+1=3·3p=3（4m-1）=4（3m-1）+1∉ ｛an｝，bp+2=9·3p=9（4m-1）=4（9m-2）-1∈ ｛an｝，所以 cn+1=bp+2，cn=又 c1=3，∴cn=3·9n-1=32n-1。

解二：利用二项式定理

设 cn=am=bp，即 cn=4m-1=3p，

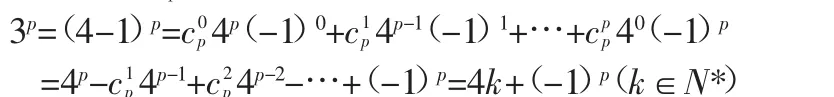
当 p 为奇数时，4k+（-1）p=4k-1，即数列 ｛bn｝的奇数项由小到大排成数列 ｛cn｝，所以 cn=b2n-1=32n-1。

点评：对于解一，等比数列很明显在n的值相同的情况下在数值上比等差数列增幅大，所以公共项从第二项起，应该考虑等比数列中哪些项是等差数列中的项，对于解二，问题转化为求p，m的不定方程，利用二项式定理求解。

三、等差数列与多项式数列的公共项问题

例：数列 ｛an｝与 ｛bn｝的通项公式分别为an=5n+4，bn=n2，它们的公共项从小到大排成新的数列 ｛cn｝，求 ｛cn｝的通项公式。

解：设等差数列 ｛an｝的第m项与等比数列 ｛bn｝的第p项相等，即 cn=am=bp，即 cn=5m+4=p2，m=考虑 p=5k-4，5k-3，5k-2，5k-1，5k 时，分情况讨论：

当p=5k时，m=5k2-∉N*；当 p=5k-1时，m=5k2-2k-3∉N*；5

当 p=5k-2 时，m=5k2-4k∈N*；当p=5k-3时，m=5k2-6k+1∈N*；

当p=5k-4时，m=5k2-8k+∉N*，故当 p=5k-2，p=5k-3时，m为正整数。

故 ｛cn｝中的项依次为：b2，b3，b7，b8，b12，b13，…，｛cn｝中的奇数项依次是 b2，b7，b12，b17，…下标是以 5 为公差的等差数列；｛cn｝中的偶数项依次是 b3，b8，b13，b18，…下标是以 5 为公差的等差数列；当n 为奇数时，c2k-1=［2+（k-1）×5］2=（5k-3）2，当 n 为偶数时，c2k=［9+（k-1）×5］2=（5k+4）2；所以 cn=

点评：根据本题的解题思路，可以很快找到规律解决以下问题。如数列an=3n+1，bn=n2，公共项构成新数列 ｛cn｝：b2，b4，b5，b7，b8，b10，…；再如数列 an=7n+2，bn=n2，公共项构成新数列 ｛cn｝：b3，b4，b10，b11，b17，b18，…。故对于等差数列 an=pn+q，bn=n2，首先通过计算两个数列前p项中公共项，假设为bi，bj，则构成的新数列 ｛cn｝：bi，bj，bi+p，bj+p，bi+2p，bj+2p，bi+3p，bj+3p，…，奇数项及偶数项下标分别构成以p为公差的等差数列，这样就易算出新数列的通项公式。

［1］陈素贞，陈丽美.中国剩余定理在求一类等差数列公共项问题的应用［J］.福建中学数学，2008（12）.

［2］戴亚宁.浅议两个数列的公共项［J］.中学数学月刊，2000（9）.