公倍数
杨小容
教学内容:
教科书12页例2,第13页课堂活动第2题,练习四第4题。
教学目标:
1.了解公倍数和最小公倍数的意义,掌握求两个自然数的最小公倍数的方法。
2.通过解决实际问题,初步了解两个数的公倍数和最小公倍数在现实生活中的应用。
3.培养学生抽象、概括的能力,增强学生学习数学的信心。
教学重点:
了解公倍数和最小公倍数的意义,掌握求两个自然数的最小公倍数的方法。
掌握求两个自然数的最小公倍数的方法。
教学准备:多媒体课件
教学课程:
一、情景引入
五年级同学参加植树劳动,按15人一组或18人一组都正好分完。五年级同学参加植树的至少有多少人?
分析:(1)五年级同学按15人一组分,正好分完,说明五年级同学是15的倍数。
(2)五年级同学按18人一组分,正好分完,说明五年级同学是18的倍数。所以五年级同学既是15的倍数,又是18的倍数。我们叫它是15和18的公倍数。这节课我们就来学习公倍数。板书课题(公倍数)
二、探究新知
写出4和6的倍数
找一找,想一想,你发现了什么?
12,24,36,48,…既是4的倍数,又是6的倍数。12,24,36,48,…是4和6公有的倍数,叫做4和6的公倍数。12是公倍数中最小的,叫做它们的最小公倍数。
练习:书上第13页课堂活动第2题
想一想:有最大公倍数吗?其他公倍数与最小公倍数有什么关系?
找最小公倍数就很重要。
列举法可以求两个数的公倍数,数大用列举法就不方便,如9和47的公倍数 。
观察一个数的倍数与这个数的质因数的关系?
4的倍数:4=2×2, 8=2×2×2, 12=2×2×3, 16=2×2×2×2,20=2×2×5,
24=2×2×2×3,28=2×2×7,…
4分解成质因数的乘积 4=2×2
6的倍数:6=2×3,12=2×2×3,18=2×3×3,24=2×2×2×3,30=2×3×5,36=2×2×3×3,…
6分解成质因数的乘积 6=2×3
最小公倍数2×2×3=12
归纳:一个数的倍数必须包含这个数所有的质因数
把数写成质因数的乘积形式用到了短除法,我们也可以用短除法求最小公倍数。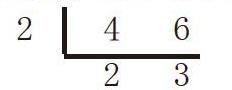
练习: 1.用短除法求6和9的最小公倍数
2.解决情景引入:五年级同学参加植树劳动,按15人一組或18人一组都正好分完。五年级同学参加植树的至少有多少人?
3.求下面每组数的最小公倍数。
从中你发现了什么?
归纳:用短除法求两个数的最小公倍数:
如果两个数的最大公因数是1,那么这两个数的积就是它们的最小公倍数。
如果较大数是较小数的倍数,那么较大数就是这两个数的最小公倍数。
三、课堂小结
求两个数的最小公倍数的方法:
1. 列举法
先把两个数的倍数写出来,再从两个数的倍数中找出两个数的公倍数,最后找出两个数的最小公倍数。
2. 质因数分解法
先把这两个数分解质因数,再找到它们公有的质因数,最后把它们公有质因数与它们特有质因数的积相乘。就得到这两个数的最小公倍数。
3. 短除法
先找出这两个数的公因数,再把公因数与它们特有质因数的积相乘。
四、板书设计
1.公倍数、最小公倍数
2.求最小公倍数的方法。
五、教学反思
整节课取得良好的教学效果。但由于该上课了,结果录不起课,耽搁了20分钟才开始录课,在时间上就没把握好,重点强调用短除法找最小公倍数,安排找规律的时间少了,没有让学生得到充分的思考。

