一类连续型单参数指数族参数的经验Bayes双侧检验

黄金超

（滁州职业技术学院 基础部，安徽 滁州 239000）

0 引言

单参数指数族参数的经验Bayes（EB）检验问题,在以往文献中已有非常多的研究，如文献[1-7]等对其做了不同程度的研究，并取得有意义的结果，彭家龙等[8]在“线性损失”下研究了一类连续型单参数指数族参数的经验Bayes单侧检验，但是目前几乎所有研究单参数指数族EB检验问题的文献，都是利用密度函数的普通核估计来构造参数的EB检验。本文将在“平方损失”下利用密度函数的递归核估计来研究一类广义单参数指数族参数的经EB双侧检验问题。本文采用“平方损失”和递归核估计，研究参数的双侧检验。

设随机变量X条件概率密度[8]：

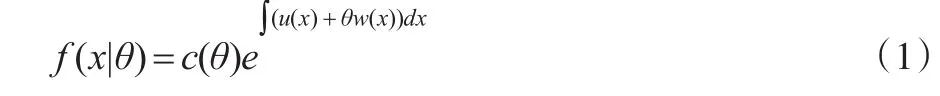
这里u（x）和w（x）为连续函数，不妨设u（x）＞0和 w（x）＜0，样本空间为参数空间为

本文考虑分布族式（1）中参数θ的如下EB双侧检验：

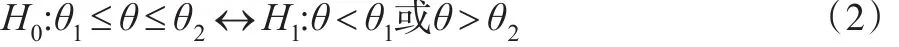
此处θ1和θ2为已知正常数，若取和则双侧检验式（2）等价于：

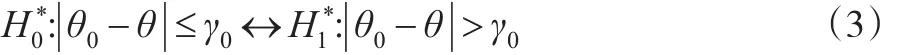
对假设检验式（3），取下列“平方损失”函数为：

δ（x）=P（接受H0|X=x） （5）

为随机化判别函数，则在先验分布 G（θ）下 δ（x）的Bayes风险函数为：

其中：

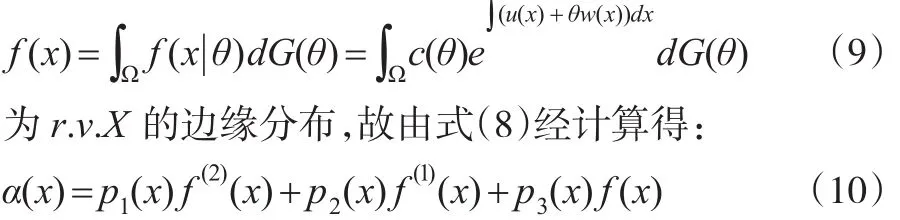
其中 f（1）（x），f（2）（x）分别表示 f（x）的一阶，二阶导数，且：

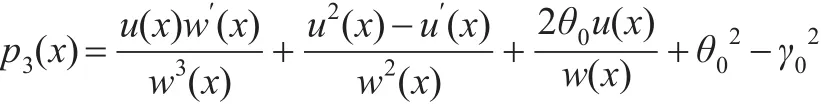
由式（6）易见Bayes判决函数为：

其Bayes风险为：

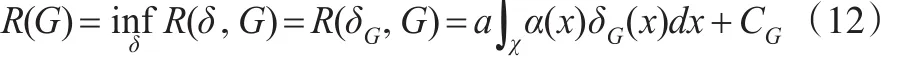
上述风险当 G（θ）已知，且 δ（x）=δG（x）是可以精确达到的，但此处G（θ）未知，因而 δG（x）不能使用，于是考虑引入EB方法。

1 EB检验函数的构造

假定Cs，α，为R1中一族概率密度函数，其s阶导数存在，且| |

f（x）≤α α，s＞4为正整数。令 Kr（x）（r=0，1，…，s-1）是 Borel可测的有界函数，在区间（0，1）之外为0，且满足条件（B）

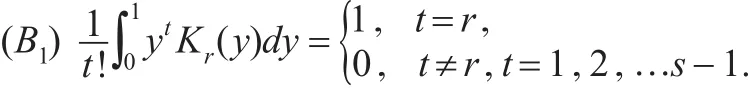
（B2）Kr（x）在R1上除有限点集E0外是可微的，

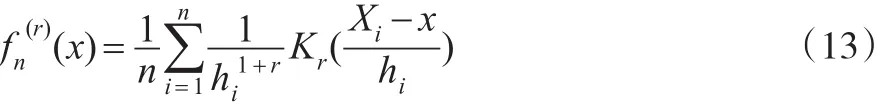
其中 hn↓0，Kr（x）是满足条件 （B）的核函数，经计算得：

由上式可知此估计具有一种递归性质，用递归核估计去估计 f（r）（x）时，由于可以进行递归计算，在样本点的增加情形下不需要重新计算所有项，仅计算新的添加项，如果用普通的核估计就必须重新计算所有项，因此采用递归核估计可以减少计算量。其次，递归核估计对不同区间可以选择不同的适当窗宽，从而可以克服估计的过度平滑和过度锐化，这样能够较为全面地刻画密度函数，从而提高了估计的效率。

由式（10）和式（13）定义α（x）的估计量：

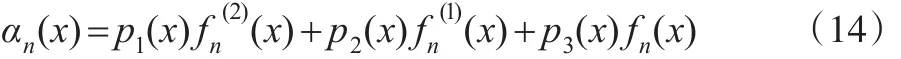
故EB检验函数定义为:

令 En表示对的联合分布求均值,则δn（x）的全面Bayes风险为：

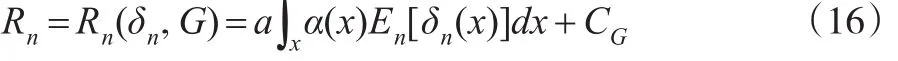
本文假定 c，c0，c1，c2… 为不依赖n的正常数。

（2）当取时,对 0＜λ≤1,则有：

证明：（1）由Cr不等式可知,对r=0,1,2有：

由式（13）和核函数的性质可知：

由Taylor展开得：

将式（19）代入式（18）可得：

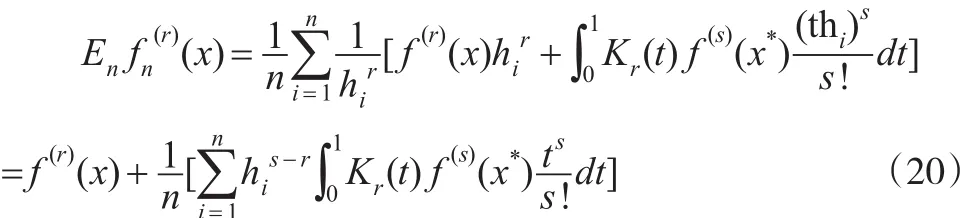
由 f（x）∈Cs，α，及| Kr（t）|≤C ，可知：

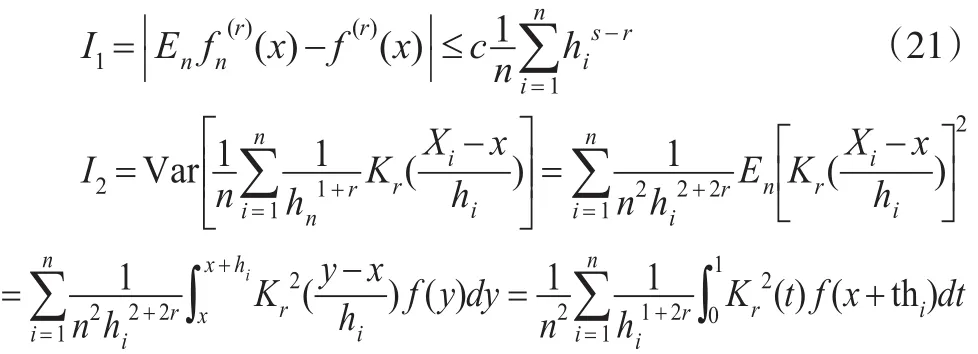
再由 f（x）∈ Cs，α，及| Kr（t）|≤M,hn单调递减=0可知：

将 式（23）和式（24）代入式（17），结论（1）成立。

（2）由Cr不等式可知：

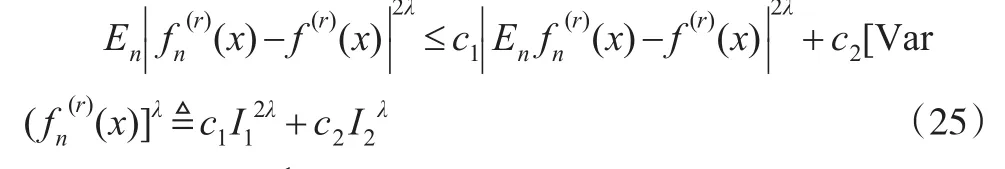
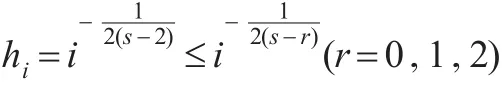
由式（21）可得：

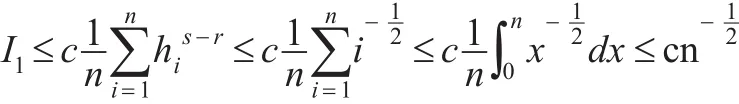
故有：

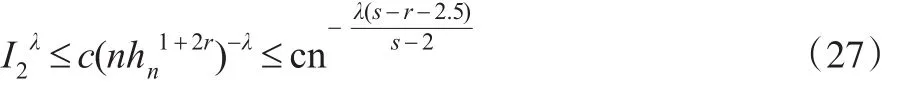
将式（26）和式（27）代入式（25），结论（2）成立。

引理2：令 R（G）和 Rn分别由式（12）和式（16）给出，则：

证明：见文献[1]引理1。

2 EB检验函数的主要结果

定理 1：设 δn（x）由式（15）给出，其中为 iid样本序列，假定条件（A）和（B）成立，若：

（3）f（r）（x）为x 的连续函数，则有

证明：由引理2可知：

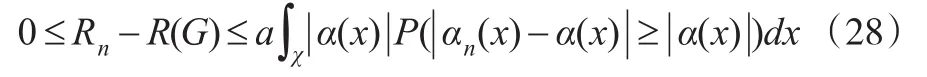
由式（8）和Fubini定理得：

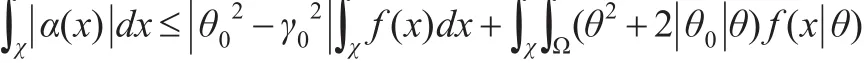
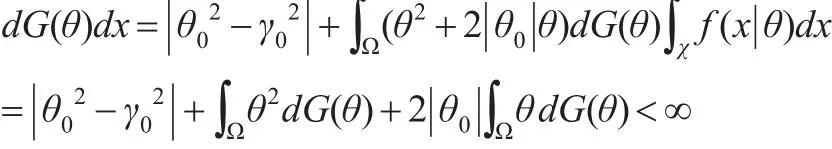
由控制收敛定理，可知：

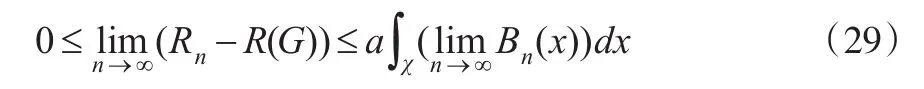
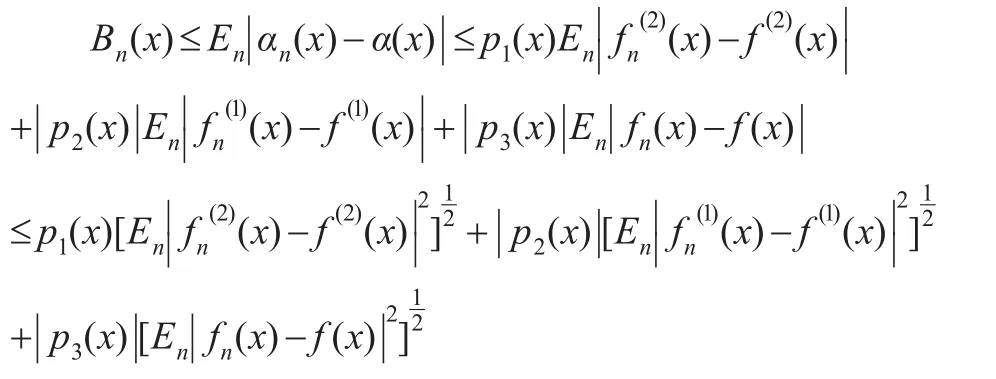
再由引理1（1）可知，对 x∈χ，当 r=0，1，2时有：

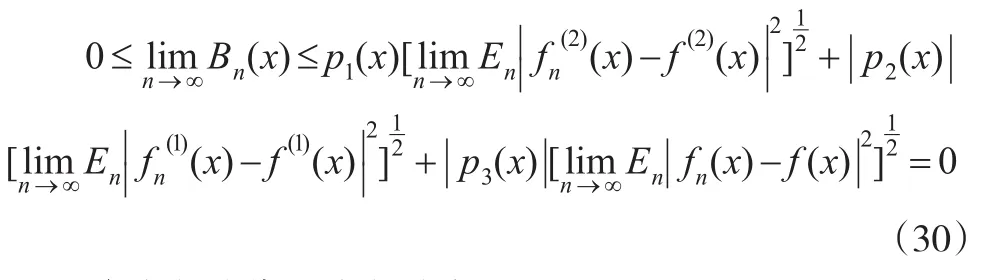
将式（30）代入式（29）定理得证。

定理2：设 δn（x）由式（15）定义,其中 X1，X2，…，Xn为iid样本序列,且假定（A和（B）成立,若0＜λ＜1,有：

证明：由引理2和Markov不等式，可知：

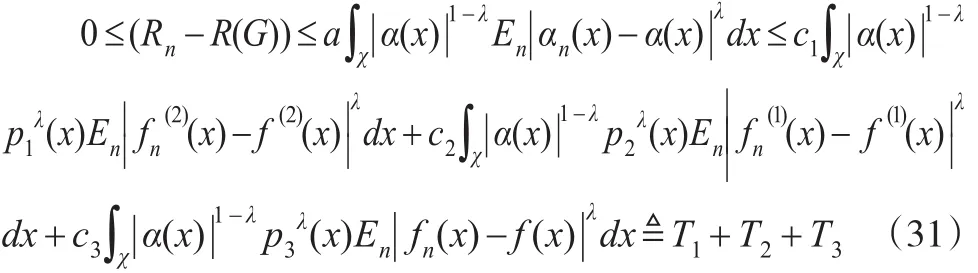
由引理1（2）可知：

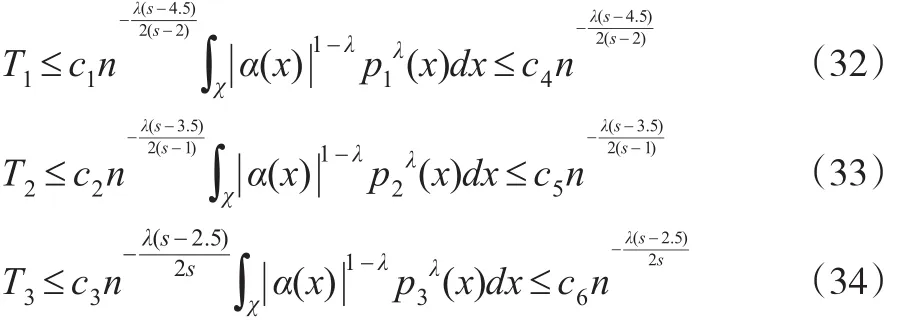
将式（32）至式（34）代入式（31）定理得证。

3 例子

下面举例验证适合文中定理1与定理2条件的分布族和先验分布是存在的，在模型式（1）中，令 c（θ）=θ，u（x）=0，w（x）=-1，则随机变量X分布为取 θ 的先验分布为Gamma分布族：

β和r为已知常数β＞0，r＞0.所以有：

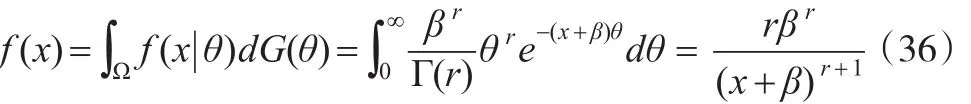
因此：

（1）由式（36）易见 f（x）为 x任意阶可导连续且一致有界，即 f（x）∈Cs，α。

由于 β＞0，r＞0，这一积分为第1类广义积分，当 （r+1）（1-λ）＞1时，即上述积分收敛。

由（1）—（3）可知，定理1和定理2条件均成立。

4 结论

本文在“平方损失”下，研究了一类广义单参数指数分布族参数的经验Bayes（EB）双侧检验问题，利用概率密度函数的递归核估计，构造了参数的EB检验函数，本文采用“平方损失”和递归核估计，研究了相应参数的双侧检验，这与以往研究单参数指数分布族参数的EB检验的文献不同，本文在适当的条件下，证明了所提出的EB检验函数的渐近最优（a.o.）性，获得了其收敛速度的阶可任意接近于推广现有文献的相应结果，并给出满足条件结果的一个例子。

[1]Johns M V Jr,Van Ryzin J.Convergence Rates in Empirical Bayes Two-action ProblemsⅡ:Continuous Case[J].Ann.Math.Statist,,1972,（42）.

[2]Van Houwelingen J C.Monotone empirical Bayes Test for the Continu⁃ous One-Parameter Exponential Family[J].Ann.Statist.,1976,（4）.

[3]Liang Tachen.On empirical Bayes Tests in a Positive Exponential Family[J].Journal of Statistical Planning and Inference,2000,（83）.

[4]Liang Tachen.On Optimal Convergence Rate of Empirical Bayes Tests[J].Statistics&Probability Letters,2004，（68）.

[5]韦来生.刻度指数族参数的经验Bayes检验问题NA样本情形[J].应用数学学报,2000,（23）.

[6]周雁,韦来生.刻度指数族参数的经验Bayes检验函数收敛速度的改进[J].高校应用数学学报,2008,23（2）.

[7]陈家清,刘次华.线性指数分布族参数的经验Bayes检验问题[J].系统科学与数学,2008,28（5）.

[8]彭家龙,袁莹.一类连续型单参数指数族参数的经验Bayes检验问题[J].高校应用数学学报,2012,27（4）.

[9]樊家琨.概率密度函数及其导数递归核估计的强相合性[J].河南大学学报：自然科学版,1992,22（2）.